
균등 분포 (Uniform Distribution)
2020. 3. 16. 16:10
✏️ Mathemathics/Statistics and Probability
밀도함수의 면적은 곧 확률이다. 밀도함수의 면적을 적분 = 면적 = 확률 분포함수 는 항상 누적이란 말을 앞에 생략해 놓는다 : 누적분포함수 (x-1)/4은 x까지의 누적 확률이다. 참 쉽죠?

확률과 통계2 1주 1강
2020. 3. 16. 16:04
✏️ Mathemathics/Statistics and Probability
중간 - 100점 기말 - 100점 과제 - 20점 (2회) 퀴즈 - 40점 출석 - 10점 중간, 기말 합 40점 미만 F 내가 이 프로그램을 개발했을 때 테스트 해볼 때 가설 검정을 해야한다. 표준화라는 것은 평균을 0으로 하고 분산을 1로 하는 것이다. 표준화 하는 방법 : X - E(X)/루트분산
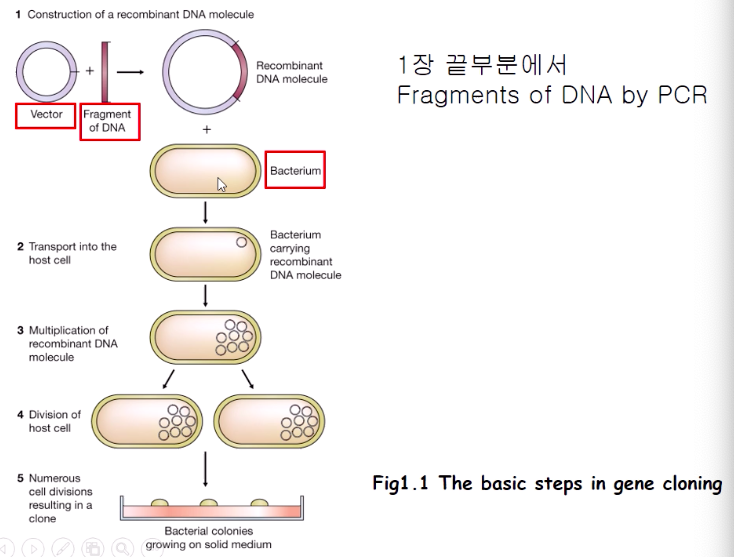
유전공학 2장 - Vehicles for gene cloning
2020. 3. 16. 13:07
🧬 Bio/유전공학
★★★★★★★ Cloning Vector 조건 복제가 가능해야한다. Selection marker를 가져야 한다. 10kb 이하여야 한다. 박테리아에 넣게 플라스미드 selection marker 지닌다 : Antibiotic resistance replication origin이 있다. Copy number를 조절할 수 있다. conjuction을 통해 전달이 가능하다. 독립적으로 존재한다. 복제 방법 Non-integrative plasmid : 숙주의 DNA polymerase 사용 Integrative plasmid (Episome) : 숙주의 염색체에 삽입돼서 복제된다. Conjugation : 가까이 연접해서 recombinant DNA가 복제되는 것 전달될 수 있는 유전자를 transfer ..

유전공학 1주 1회
2020. 3. 16. 11:36
🧬 Bio/유전공학
1866년에 멘델이 멘델의 법칙을 발표한다. 그래서 유전자는 유전 특성을 조절하는 인자라는 개념을 도입함 40년 동안 맨델의 유전에 대해 관심이 없다가 다시 1900년도에 멘델의 유전법칙에 관심을 갖게 된다. 멘덴의 유전법칙의 재발견 실제 유전학이라는 개념을 갖게된다. 유전학이란 것은 유전자가 어떤 일을 하는지에 대해 이해하는 학문이다. 유전공학의 역사는 유전학으로부터 시작되고 유전공학이 어떻게 발달되는지 봐보자. 멘델의 재발견이 있는 다음부터 약 30년동안 서튼이라는 사람이 염색체 설이라는 것을 내놓는다. 유전자가 염색체에 의해 전달 된다. 모건이 염색체가 유전이라는 것에 기여한다는 것을 밝혀내면서 노벨상 탄다. 유전자 지도를 작성함 모건은 초파리 갖고 실험한다. 유전적 거리 = 모건 unit 300~..
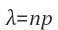
포아송 분포 (Poisson Distribution)
2020. 3. 12. 17:11
✏️ Mathemathics/Statistics and Probability
1. 정의 포아송 분포에 붙은 '포아송'은 사람의 이름이다. 포아송은 1791년 프랑스에서 태어났다. 그의 직업은 공학자, 수학자, 물리학자였다. 기계나 재료를 전공한 분이라면 반드시 들어보았을 포아송비(poisson's ratio)도 이분이 만들었다. 에펠탑에 이름이 새겨진 72명의 과학자 중 한명이라고 한다. 포아송분포는 이항분포의 특수한 경우로 생각할 수 있다. 이항분포에서 시행횟수가 무수히 많아지고, 발생확률은 아주 작은 경우이다. 한가지 의문이 든다. 그럼 그냥 이항분포로 계산하면 되지, 왜 굳이 포아송분포가 필요한거야? 이 의문을 해결해 보자. 거리를 돌아다니다가 길냥이를 본 적이 있을 것이다. 하루종일 거리를 돌아다니다 마주치는 길냥이의 수를 확률변수로 놓고 확률분포를 구해보자. 길냥이를 마..
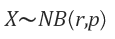
음이항 분포(Negative Binomial Distribution)
2020. 3. 12. 13:09
✏️ Mathemathics/Statistics and Probability
목차 음이항 분포의 정의 예시 일반화 평균 분산 그래프 이름의 유래 1. 음이항 분포의 정의 이미 배운 기하분포를 떠올려 보자. 음이항 분포는 기하분포의 확장이라고 볼 수 있다. 더 정확히 말하면 음이항 분포의 여러 정의 중 하나가 기하분포의 확정버전이다. 기하분포의 정의는 이랬다. 성송확률을 p라고 했을 때, x번째 시행에서 처음으로 성공할 확률 p(x)의 분포 이 정의를 k번째로 바꾸면 된다. 성공확률을 p라고 했을 때, x번째 시행에서 k번째 성공이 나올 확률 p(x)의 분포 위 음이항분포를 보면, 사전에 정의되어야할 값이 성공확률 p말고 k도 있다. p와 k가 정해져야 확률분포함수가 정의된다는 말이다. 그러나 음이항 분포는 위의 정의 말고 또 다른 정의가 있다. 위의 정의는 일반적인 음이항 분포의..
java - class, public class 차이
2020. 3. 10. 22:31
📌 java/java
Program.java 라는 이름을 가진 클래스 파일로 예시를 들어보자. Program.java class Program { } 문제없이 컴파일이 잘 된다. 위 소스 파일에 아래와 같은 클래스를 하나 더 추가해보자. class Program { { class Program2 { } 역시나 문제없이 컴파일이 잘 된다. 그렇다면 아래와 같이 수정을 해보자. class Program { } public class Program2 { } Program2라는 클래스 앞에 public이라는 접근제어자를 붙였더니 이번에는 컴파일 에러가 발생한다. 그럼 아래와 같이 수정을 해보자. public class Program { } class Program2 { } 문제없이 컴파일이 잘 된다. 어떤 차이일까? 위와 같이 컴파..
java - 패키지
2020. 3. 10. 22:21
📌 java/java
패키지는 여러 사람이 만들기 때문에 이름이 중복될 수 있다. 이름의 중복을 피하기위한 방법을 찾아보자. 나한테 원래 java.txt가 있는데 누군가 나에게 java.txt라는 파일을 줬을 때 이름이 겹치는데 그때 필요한게 디렉토리이다. a 디렉토리의 java.txt가 존재해도 b 디렉토리의 java.txt가 존재할 수 있다. 전역변수와 지역변수도 이 이름의 충돌을 해소하기 위한 하나의 수단으로 볼 수 있다. 패키지 만들기 우리는 이미 패키지를 사용해왔다. 일부 IDE들은 패키지의 사용을 강제하고 있기 때문에 독자가 패키지가 무엇인지도 숙지하지 않은 상태에서 패키지를 사용한 것이다. 주제에서 어긋나는 이야기이지만 지식이라는 것이 사실은 순차적이지 않고 네트워크적이라는 점을 생각해볼 필요가 있다. 순차적인 ..

java - 클래스 패스, 환경 변수 [참고용]
2020. 3. 10. 21:30
📌 java/java
클래스 패스 클래스가 위치하는 경로를 우리가 지정해서 자바가 필요로 하는 어떤 클래스를 로드하는 방법을 지정하는 것이 클래스 패스이다. 빈 디렉터리에 아래와 같이 코드를 작성한다. 필자는 프로젝트 디렉토리에 /srcbin 이라는 디렉토리를 만들고 여기에서 실습을 진행할 것이다. 아래 예제의 파일명은 ClasspathDemo.java 이다. class Item{ } class ClasspathDemo { } 컴파일을 한다. javac ClasspathDemo.java 그 결과 두 개의 클래스 파일이 생성된다. ClasspathDemo.class Item.class 즉 클래스 하나는 하나의 클래스 파일이 된다는 것을 알 수 있다. 클래스의 경로 ClasspathDemo2.java을 만들고 내용을 아래와 같이..

java - overloading
2020. 3. 10. 11:33
📌 java/java
overloading 계산기 예제로 돌아가보자. 우리의 계산기는 2개의 값(left, right)에 대한 연산(sum, avg) 만을 수행 할 수 있다. 그런데 만약 3개의 값을 대상으로 연산을 해야 한다면 어떻게 해야할까? 우선 아래와 같이 입력값을 3개 받아야 할 것이다. c1.setOprands(10, 20, 30); 이를 위해서 기존의 setOprands 메소드를 아래와 같은 모습을 수정한다면 2개의 입력값을 받을 수 없게 될 것이다. public void setOprands(int left, int right, int third){ this.left = left; this.right = right; this.third = third; } 이런 경우 아래와 같이 메소드의 이름을 변경하면 될 것이다..

java - overriding
2020. 3. 9. 22:34
📌 java/java
창의적인 상속 상속은 상위 클래스의 기능을 하위 클래스에게 물려주는 기능이다. 그렇다면 하위 클래스는 상위 클래스의 메소드를 주어진 그대로 사용해야 할까? 만약 그래야 한다면 제약이 상당할 것이다. 어떤 메쏘드에 대해서는 자식클래스 만의 독자적인 메쏘드를 정의해야할 필요가 있다. 부모가 가지고 있는 메쏘드를 물려받긴 했지만 자식 클래스의 필요에 따라서 부모 클래스의 메쏘드를 변경하는 방법이 overriding이다. 이런 제약을 벗어나려면 하위 클래스가 부모 클래스의 기본적인 동작방법을 변경할 수 있어야 한다. 이런 맥락에서 도입된 기능이 메소드 오버라이딩(overriding)이다. 상속 시간의 예제를 살펴보자. 이 예제는 클래스 Calculator의 기본적인 동작 방법을 상속 받은 Substraction..
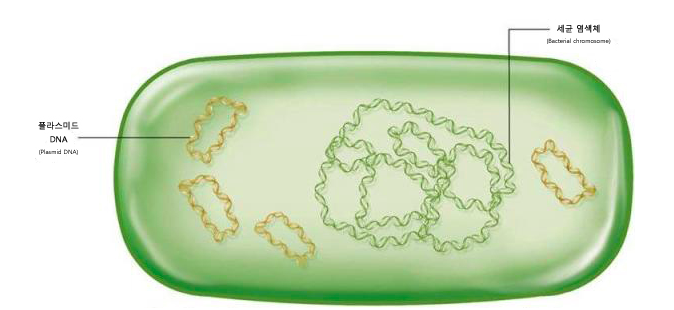
Plasmid DNA란?
2020. 3. 9. 21:22
🧬 Bio/생명공학
목차 Plasmid DNA란? Vector DNA로써 Plasmid DNA의 구조적 특징 기능에 따른 Plasmid 분류 Plasmid DNA의 conformation(형태) Plasmid DNA란? 원핵생물과 일부 진핵생물이 자신의 염색체 DNA(위 그림에는 Bacterial DNA로 표시된 것) 외에 가지고 있는 작은 고리형 DNA를 말한다. 예를 들면, 대장균은 대장균 자신의 염색체 DNA(chromosomal DNA)가 있고, 크기가 더 작은 고리 모양의 또다른 DNA(circular DNA)가 있는 경우가 있다. 재밌는 건, 대장균과 같은 원핵생물의 경우 염색체 DNA도 플라스미드처럼 고리 모양이라는 것이다. 다만 그 크기가 크기 때문에 세포내에서 꼬여있는 상태로 존재한다 (윗 그림에도, Bac..
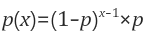
기하 분포 (Geometric distribution)
2020. 3. 9. 18:13
✏️ Mathemathics/Statistics and Probability
1. 정의 베르누이 시행을 반복할 때, 처음 성공이 나오기까지 시행한 횟수를 확률변수 X로 할 때의 확률분포 이다. 예를 들어 확률변수 4의 확률은 "실패-실패-실패-성공"인 경우의 확률이다. 또 다른 정의도 있는데 , 처음 성공이 나오기까지 실패한 횟수를 확률변수로 하는 경우도 있다. 2. 예시 연애를 시작한 남녀가 결혼할 확률은 5퍼센트라고 가정하자. x번째 사귄 이성과 결혼하게 될 확률분포가 기하분포이다. 3. 일반화 어떤 사건이 발생할 확률을 p라고 하자. 사건이 발생하지 않을 확률은 1-p이다. 성공과 실패로 봐도 된다. 이때 기하분포는 아래와 같다. 확률변수 x는 모두 자연수이다. x = 성공할때까지의 시행 횟수 기호로는 아래와 같이 나타낸다. 4. 통계량 (1) 평균 시그마를 전개해 보자. ..
Gene Cloning
2020. 3. 9. 17:10
🧬 Bio/생명공학
Vector(벡터) 벡터란 플라스미드나 박테리오파지와 같은 DNA로서 세포 형질전환을 통해 특정 유전자나 DNA를 자신에게 삽입시켜 재조합 DNA를 만든 후 이것을 숙주세포로 전달하여 많은 수로 복제 될 수 있도록 하거나 또는 단백질로 발현될 수 있도록 하는 DNA운반체를 말한다. Vector의 조건 사본(copy)수가 많아야한다. 간단히 분리 및 정제가 가능해야 한다. 불필요한 유전정보를 최소화하여 작은 DNA로부터 외부 유전자 DNA를 클로닝 할 수 있어야한다. 복제 원점을 가지고, 숙주세포에서 독립적인 복제가 가능해야 한다. 제한효소 자리 집단(Multiple Clonning Site, MCS)이 있어야 한다. 선발 표지자(selection marker)가 있어야 한다. Clonning Vector..
PCR (Polymerase Chain Reaction)
2020. 3. 9. 16:51
🧬 Bio/생명공학
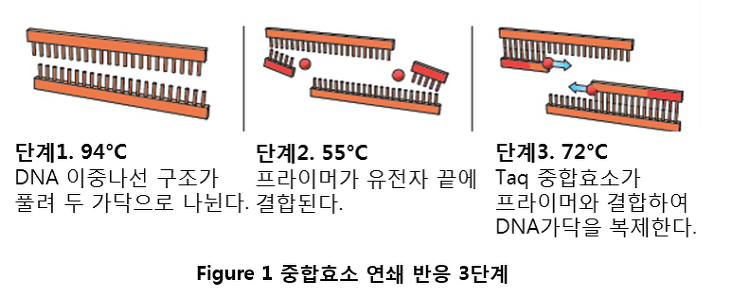
PCR (Polymerase Chain Reaction, 중합효소 연쇄반응) 중합효소 연쇄 반응(polymerase chain reaction, PCR)은 캐리 멀리스(Kary B. Mullis)에 의하여 1985년에 개발되어 현재 유전물질을 조작하여 실험하는 거의 모든 과정에 사용하고 있는 검사법으로, 검출을 원하는 특정 표적 유전물질을 증폭하는 방법입니다. 중합효소 연쇄 반응에 의해, 소량의 유전물질로부터 염기 순서가 동일한 유전물질을 많은 양으로 증폭할 수 있으므로, 인간의 DNA를 증폭하여 여러 종류의 유전질환을 진단하는 데 사용됩니다. 또한 세균이나 바이러스, 진균의 DNA에 적용하여 감염성 질환의 진단 등에 사용할 수 있습니다. 중합효소 연쇄 반응의 순서는 3단계로 이루어집니다. 열을 이용하여..
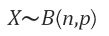
이항 분포 (Binomial Distribution)
2020. 3. 9. 16:06
✏️ Mathemathics/Statistics and Probability
1. 정의 베르누이 시행을 n번 했다. 각 시행이 독립이라는 것은 베르누이 시행 조건중 하나이다. 따라서 베르누이 시행이라고 하면 따로 독립을 언급할 필요가 없다. 이 시행에서 발생할 확률을 p라고 하자. 사건이 발생한 횟수를 확률변수 x로 했을 때의 분포가 이항분포이다 2. 예시 3. 일반화 어떤 독립시행에서 특정 사건이 발생할 확률은 p이다. 이 시행을 n번 했을 때, 사건이 발생할 횟수를 x라고 하자. 이 때의 확률 분포가 이항분포이고 아래와 같다. 시행 횟수가 n, 사건 발생 확률이 p인 이항분포를 기호로 표현하면 아래와 같다. B는 binomial의 약자이다. 4. 통계랑 (1) 평균 구하기 x가 0일 때는 값이 0이므로 시그마의 시작을 1부터로 바꿀 수 있다. 아래와 같이 변형하자. p와 n은..