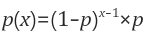
1. 정의
베르누이 시행을 반복할 때, 처음 성공이 나오기까지 시행한 횟수를 확률변수 X로 할 때의 확률분포 이다.
예를 들어 확률변수 4의 확률은 "실패-실패-실패-성공"인 경우의 확률이다.
또 다른 정의도 있는데 , 처음 성공이 나오기까지 실패한 횟수를 확률변수로 하는 경우도 있다.
2. 예시
연애를 시작한 남녀가 결혼할 확률은 5퍼센트라고 가정하자.
x번째 사귄 이성과 결혼하게 될 확률분포가 기하분포이다.

3. 일반화
어떤 사건이 발생할 확률을 p라고 하자. 사건이 발생하지 않을 확률은 1-p이다.
성공과 실패로 봐도 된다.
이때 기하분포는 아래와 같다. 확률변수 x는 모두 자연수이다.
x = 성공할때까지의 시행 횟수
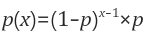
기호로는 아래와 같이 나타낸다.

4. 통계량
(1) 평균

시그마를 전개해 보자. 확률변수는 모두 자연수이기 때문에 극한이 등장한다. 아래 식을 1번식이라고 하자.

(1-p)를 양변에 곱해서 식을 하나 더 만들자.

1번식에서 2번식을 빼보자.

p는 약분된다.
빨간 부분은 등비수열이다. 등비수열의 합을 구해보자.

두항 모두 수렴하기 때문에 극한을 분리해서 쓸 수 있다.

첫 항은 1/p 로 수렴한다. 두번째 항은 0으로 수렴한다. 로피탈 정리를 이용하면 된다.
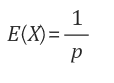
요약하자면 어떤 확률변수 x가 기하분포를 따르고 성공할 확률이 p 일때, 이 확률변수 x의 평균은 1/p이다.
(2) 분산

5. 그래프

성광확률이 클수록 시행횟수가 많아지면 확률이 낮아진다.
6. 이름의 유래
선, 곡선, 도형에서 왔다.
변의 길이의 평균
등비 수열과 모양이 매우 흡사하다
https://www.youtube.com/watch?v=jCaSVHE7Y-o&list=PLmljWRabIwWDCLjAMfTPigyTe-jtsLca1&index=10
'✏️ Mathemathics > Statistics and Probability' 카테고리의 다른 글
| 포아송 분포 (Poisson Distribution) (0) | 2020.03.12 |
|---|---|
| 음이항 분포(Negative Binomial Distribution) (0) | 2020.03.12 |
| 이항 분포 (Binomial Distribution) (0) | 2020.03.09 |
| 베르누이 분포 (0) | 2020.03.09 |
| t-분포 (0) | 2020.02.05 |