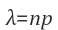
1. 1. 정의
포아송 분포에 붙은 '포아송'은 사람의 이름이다.
포아송은 1791년 프랑스에서 태어났다. 그의 직업은 공학자, 수학자, 물리학자였다.
기계나 재료를 전공한 분이라면 반드시 들어보았을 포아송비(poisson's ratio)도 이분이 만들었다.
에펠탑에 이름이 새겨진 72명의 과학자 중 한명이라고 한다.
포아송분포는 이항분포의 특수한 경우로 생각할 수 있다.
이항분포에서 시행횟수가 무수히 많아지고, 발생확률은 아주 작은 경우이다.
한가지 의문이 든다.
그럼 그냥 이항분포로 계산하면 되지, 왜 굳이 포아송분포가 필요한거야?
이 의문을 해결해 보자.
거리를 돌아다니다가 길냥이를 본 적이 있을 것이다.
하루종일 거리를 돌아다니다 마주치는 길냥이의 수를 확률변수로 놓고 확률분포를 구해보자.
길냥이를 마주칠 확률을 p라고 놓고, 시행 횟수를 n이라고 놓자.
확률을 구할 수 있나? 무지 작다는 정도만 안다.
시행횟수는 몇번인가? 길냥이를 마주치려는 시도는 걸어다니는 내내 매 순간이다.
시행횟수를 정의할 수가 없다. 확률이 있고, 시행이긴 한데 둘다 정의할 수가 없다.
그런데, 이건 정의할 수 있다.
바로 np이다.
np는 이항분포의 평균이다. 우리의 상황에서 np는 아래와 같다.
np = 하루종일 돌아다니며 길냥이를 마주치는 평균 횟수
이건 구할 수 있다.
이 값을 람다라고 놓자

포아송 분포에서 n과 p를 각각 다루지 않는다. 그럴 수 없어서 나온 분포니까.
포아송 분포에서는 람다를 다룬다.
포아송 분포의 다른 예들이다.
- 책에서 발견되는 오타 수
- 치킨을 먹다가 발견되는 머리카락 수
- 커피를 마시다가 실수로 쏟는 횟수
- 기계가 고장나는 횟수
2. 2. 이항분포로부터 유도
이항분포 함수는 아래와 같다.

포아송 분포는 n과 p를 각각 다루지 않고, 이항분포의 평균인 np를 다룬다.
이 값을 람다라고 놓는다.

아래와 같이 변형하자

이항분포 수식의 p자리에 위 식을 넣자.

조합 식을 팩토리얼로 전개하자.

위 식의 빨간 항을 아래와 같이 나눠서 써준다.

팩토리얼 식 아래와 같이 변형한다.

파란 부분끼리 약분해 준다.

x 팩토리얼과, n의 x승의 자리를 바꿔준다.

위 식의 파란 부분을 아래와 같이 변형하자.

이번에는 아래 식을 보자.

몇개의 인수가 곱해져 있는 걸까?
n! 을 (n-x)! 으로 나눈 것인데, n!의 인수는 n개 이다.
(n-x)!의 인수는 (n-x)개 이다.
n개에서 (n-x)개를 약분하면, x개가 남는다.
따라서 우리가 전개하던 수식은 아래와 같이 변형된다.

n을 무한대로 보내보자.

위 식의 빨강부분은 각 항이 모두 1로 수렴한다.
파란색 항도 n이 무한대로 가니까
괄호안이 1로 수렴하고, 1의 -x는 1이니까 1이 된다.
문제는 초록항이다.

고등학교 떄, 자연 상수 e를 배운 기억이 있을 것이다.
자연 상수는 아래와 같이 정의했다.

따라서 우리가 유도하던 식을 아래와 같이 변형할 수 있다.

아래와 같이 바꿔 준다.

대괄호 안이 e로 수렴한다.

따라서 포아송 분포는 아래와 같이 유도된다.

3. 3. 예시
아래와 같은 포아송 분포를 유도했다.

예시를 통해 위 식을 어떻게 사용하는지 알아보자.
증명에도 사용했던 길냥이 예시로 가보자.
하루 동안 돌아다니며 길냥이를 마주치는 평균 횟수가 3회라고 하자.
오늘 하루 동안 길냥이를 1번 마주칠 확률은 얼마일까?
위 경우는 람다가 3인 포아송 분포가 된다.

길냥이를 한 번 마주칠 확률은 x에 1을 넣어서 구하면 된다.

4. 4. 평균
포아송 분포는 람다라고 가정하고 유도한 분포이므로, 평균은 당연히 람다겠지만 확률분포의 평균을 구하는 수식으로 구해보자.
포아송 분포 평균을 구할 때 테일러 급수가 사용되므로, 먼저 테일러 급수를 알아보자. f(x)의 테일러 급수는 아래와 같다.

a가 0일 때는 매클로린 급수라고 한다.

이번에는 e^x의 매클로린 급수를 구해보자.

x자리에 람다를 대입하자

위 식을 증명에 사용할 것이다. 1번식이라고 하겠다
이제 포아송 분포의 평균을 구해보자.

x에 0을 넣으면 전체 항이 0이 되므로, x를 1부터 시작해도 된다.

아래와 같이 변형한다.

x-1을 n으로 치환하자.

빨간 식을 위에서 유도한 1번 식을 이용하여 변형하면 아래와 같다.

계산하면 아래와 같다.

5. 5. 분산

6. 6. 그래프
포아송 분포의 그래프는 아래와 같다.
람다를 5부터 70까지 키워가며 그래프를 그렸다.
세로선은 평균이다.

포아송 분포의 평균과 분산이 모두 람다이다.
람다가 커지면 평균이 커지는 것이므로 그래프가 우측으로 이동한다.
람다가 커지면 분산이 커지는 것이므로 그래프가 좌우로 퍼진다.
'✏️ Mathemathics > Statistics and Probability' 카테고리의 다른 글
| 균등 분포 (Uniform Distribution) (0) | 2020.03.16 |
|---|---|
| 확률과 통계2 1주 1강 (0) | 2020.03.16 |
| 음이항 분포(Negative Binomial Distribution) (0) | 2020.03.12 |
| 기하 분포 (Geometric distribution) (1) | 2020.03.09 |
| 이항 분포 (Binomial Distribution) (0) | 2020.03.09 |