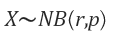
목차
- 음이항 분포의 정의
- 예시
- 일반화
- 평균
- 분산
- 그래프
- 이름의 유래
1. 음이항 분포의 정의
이미 배운 기하분포를 떠올려 보자.
음이항 분포는 기하분포의 확장이라고 볼 수 있다.
더 정확히 말하면 음이항 분포의 여러 정의 중 하나가 기하분포의 확정버전이다.
기하분포의 정의는 이랬다.
성송확률을 p라고 했을 때, x번째 시행에서 처음으로 성공할 확률 p(x)의 분포
이 정의를 k번째로 바꾸면 된다.
성공확률을 p라고 했을 때, x번째 시행에서 k번째 성공이 나올 확률 p(x)의 분포
위 음이항분포를 보면, 사전에 정의되어야할 값이 성공확률 p말고 k도 있다.
p와 k가 정해져야 확률분포함수가 정의된다는 말이다.
그러나 음이항 분포는 위의 정의 말고 또 다른 정의가 있다.
위의 정의는 일반적인 음이항 분포의 정의는 아니다. 또 위의 정의는 기하분포와의 비교를 위한 정의이다.
음이항 분포의 변수를 살펴보자.
음이항 분포에는 '시행 횟수'와 '성공 횟수'가 등장한다.
여기서 우리는 '실패 횟수'를 정의할 수 있다.
'시행 횟수'에서 '성공 횟수'를 빼면 '실패 횟수'가 된다.
'시행 횟수' = n
'성공 횟수' = k
'실패 횟수' = r
이라고 정의해 보자
n = k + r
이 중 한 값을 결정하고, 또 한 값을 변수로 놓을 수가 있다. 따라서 아래 다섯가지 경우가 가능하다.

이 중 첫 번째 정의가 일반적인 정의이다.
성공확률을 p라고 했을 때, r번의 실패가 나오기까지 발생한 성공이 k번일 확률 p(x = k)의 분포
2. 예시
어떤 농구선수의 자유투 성공률이 30%라고 해보자.
이 농구선수가 3번의 실패가 나오기까지 발생한 성공이 x번일 확률이 음이항 분포이다.
x가 0일 때부터 구해보자.
성공 없이 실패만 세번 하면 된다.

x가 1일 때는 어떨까?
실패를 3번 할 동안 성공이 1번 나오면 된다.
마지막에 실패로 끝나는 것이므로 아래와 같은 경우들이 가능하다.

확률을 구해보자

x가 2일 때도 경우를 구해보자

경우가 많아서 세기 귀찮다. 규칙을 찾아야 한다.
마지막에는 실패로 끝나니까 실패 횟수에서 하나를 빼놓는다.
위의 경우에는 3번의 실패에서 하나를 뺏기 때문에 두 번의 실패가 남는다.
거기에 성공 횟수 2회가 더해져서, 실패2성공2를 나열한 경우의 수가 된다.
조합으로 하면 C(4,2)이다. 확률을 구하면 아래와 같다.

성공 횟수를 자연수 값이 아니라 x로 놓아보자.
마지막에 실패를 한번 해야하므로 실패 하나를 빼놓는다.
성공 x회와, 실패 2회를 나열하면 된다.
조합으로 하면 C(x+2,2)이다. 확률을 구하면 아래와 같다.
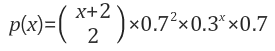
3. 일반화
어떤 사건이 발생할 확률을 p라고 하자.
r번의 실패가 나오기까지 발생한 성공이 k번일 확률 p(X = k)의 분포가 음이항 분포이다.
p와 r은 사전에 정해지는 값이다. 변수는 k이다.
이를 아래와 같이 표현한다.

k는 변수이고, r 과 p 는 주어진 값이라는 의미이다.
이제 이런 조건을 따르는 확률분포 p(X = k)를 정의하자.
k가 확률변수 x라는 의미이다. 총 r번의 실패와 k번의 성공이므로 전체 시행은 r+k번이 된다.
f(성공 ; 실패 , 성공확률)
x번 성공할 확률분포를 구할 때
r번째 실패 이전의 실패횟수는 r-1번이다.

정리해서 다시 써보자.

기호로 나타내면 아래와 같다. NB는 Negative Binomial distribution의 약자이다.
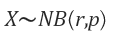
'시행 횟수' = n
'성공 횟수' = k
'실패 횟수' = r
4. 평균


5. 분산

6. 그래프
음이항 분포는 r번의 실패(사건 미발생)가 나오기까지 성공(사건발생)이 x번 발생할 확률분포이다.

r이 커질수록 평균과 분산은 커진다. p가 커질수록 평균과 분산이 커진다.
r이 커질수록 평균이 커진다는 것은 r이 커질수록 성공횟수 x가 높은 값에서 발생할 확률이 높아진다는 말이다.
r과 p가 커지면 평균, 분산이 커진다

7. 이름의 유래
먼저 이항분포 함수는 아래와 같이 생겼다.

n은 전체 시행 횟수이고 x는 성공한 횟수이다.

모양은 비슷하게 생겼다.
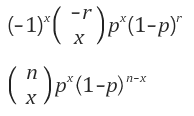
이항계수의 음수가 들어간 형태이기 때문에 음이항 분포라는 이름이 붙었다.
'✏️ Mathemathics > Statistics and Probability' 카테고리의 다른 글
| 확률과 통계2 1주 1강 (0) | 2020.03.16 |
|---|---|
| 포아송 분포 (Poisson Distribution) (0) | 2020.03.12 |
| 기하 분포 (Geometric distribution) (1) | 2020.03.09 |
| 이항 분포 (Binomial Distribution) (0) | 2020.03.09 |
| 베르누이 분포 (0) | 2020.03.09 |