1. 이진 탐색 (Binary Search) 이란?
- 탐색할 자료를 둘로 나누어 해당 데이터가 있을만한 곳을 탐색하는 방법
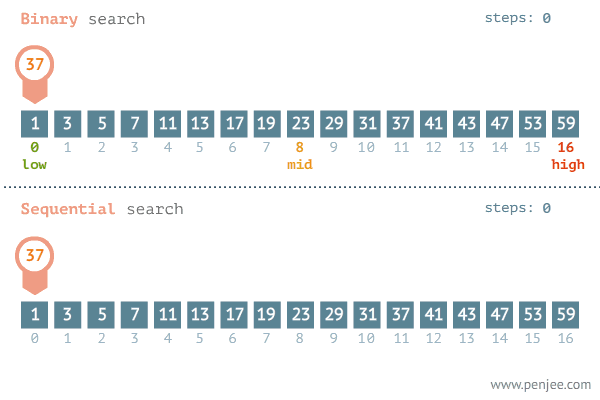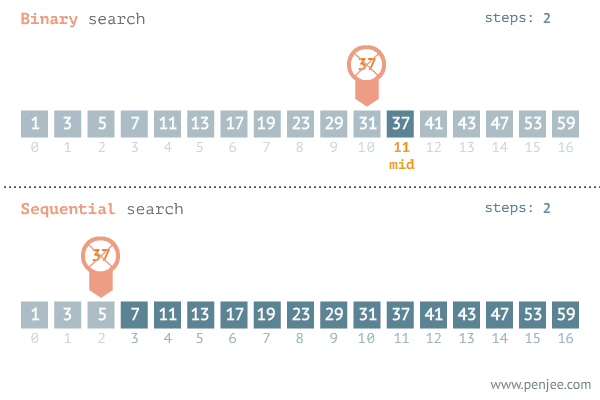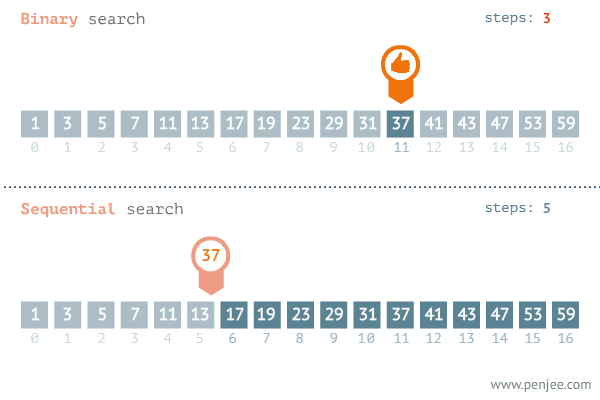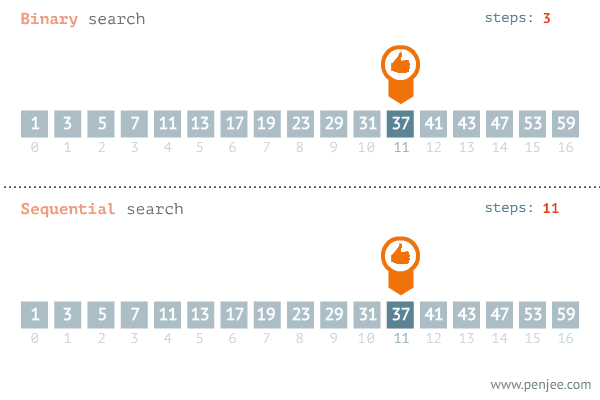
이진 탐색의 이해 (순차 탐색과 비교하며 이해하기)

데이터가 정렬되어 있다는 가정하에서는 이진탐색이 순차탐색보다 훨씬 빠르다.
2. 분할 정복 알고리즘과 이진 탐색
분할 정복 알고리즘 (Divide and Conquer)
- Divide : 문제를 하나 또는 둘 이상으로 나눈다.
- Conquer : 나눠진 문제가 충분히 작고, 해결이 가능하다면 해결하고, 그렇지 않다면 다시 나눈다.
이진 탐색
- Divide : 리스트를 두 개의 서브 리스트로 나눈다.
- Conquer
- 검색할 숫자 (search) > 중간값 이면, 뒷 부분의 서브 리스트에서 검색할 숫자를 찾는다.
- 검색할 숫자 (search) < 중간값 이면, 앞 부분의 서브 리스트에서 검색할 숫자를 찾는다.
3. 알고리즘 구현
def binary_search(data, search):
print(data)
if len(data) == 1 and search == data[0]:
return True # 검색할 데이터와 남은 데이터가 갖다면
if len(data) == 1 and search != data[0]:
return False # 검색할 데이터와 남은 데이터가 다르다면
if len(data) == 0:
return False
medium = len(data)//2
if search == data[medium]: # 데이터의 중간값과 찾는값이 같다면
return True
else: # 데이터의 중간값과 찾는값이 다르다면
if search > data[medium]: # 찾는값이 중간값보다 크다면
return binary_search(data[medium:], search)
else: # 찾는값이 중간값보다 작다면
return binary_search(data[:medium], search)
import random
data_list = random.sample(range(100), 10)
data_list
>> [69, 65, 18, 71, 11, 10, 42, 68, 36, 89]
data_list.sort()
data_list
>> [10, 11, 18, 36, 42, 65, 68, 69, 71, 89]binary_search(data_list, 66)
>> [10, 11, 18, 36, 42, 65, 68, 69, 71, 89]
>> [68, 69, 71, 89]
>> [68, 69]
>> [68]
>> False
4. 알고리즘 분석
- n개의 리스트를 매번 2로 나누어 1이 될 때까지 비교연산을 k회 진행

'🕶 Algorithm > 알고리즘' 카테고리의 다른 글
| 깊이 우선 탐색 (DFS, Depth First Search) (0) | 2021.08.08 |
|---|---|
| 너비 우선 탐색 (BFS, Breadth First Search) (0) | 2021.08.08 |
| 순차 탐색 (Sequential search) (0) | 2021.08.06 |
| 병합 정렬 (Merge sort) (0) | 2021.08.06 |
| 퀵정렬 (Quick sort) (0) | 2021.07.23 |