1. 퀵 정렬 (Quick sort) 이란?
- 정렬 알고리즘의 꽃
- 기준점(pivot 이라고 부름)을 정해서, 기준점보다 작은 데이터는 왼쪽(left), 큰 데이터는 오른쪽(right) 으로 모으는 함수를 작성함
- 각 왼쪽(left), 오른쪽(right)은 재귀용법을 사용해서 다시 동일 함수를 호출하여 위 작업을 반복함
- 함수는 왼쪽(left) + 기준점(pivot) + 오른쪽(right) 을 리턴함
- 분할 정복 알고리즘의 예이다. (재귀 사용)

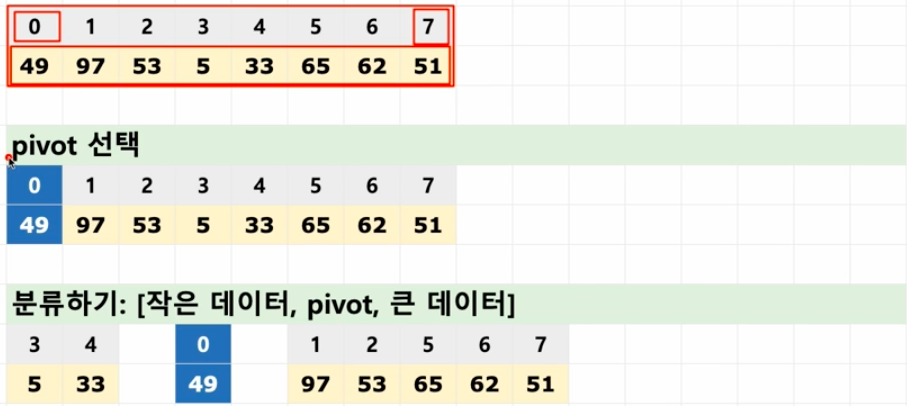
1) pivot 선택
2) [pivot보다 작은], [pivot], [pivot보다 큰] 순서대로 분류한다. (각 데이터 수 1개 될 때까지)
3) 1),2) 반복
4) 재귀적으로 합치기



다시 재귀적으로 합치기

2. 어떻게 코드로 만들까?

3. 알고리즘 구현
def qsort(data):
if len(data) <= 1:
return data
left, right = list(), list()
pivot = data[0]
for i in range(1, len(data)):
if pivot > data[i]:
left.append(data[i])
else:
right.append(data[i])
# 데이터 길이가 2 이상이면 재귀
return qsort(left) + [pivot] + qsort(right)
# pivot이라고 하면 리스트가 아니므로 [pivot]으로 해주어야 함
import random
data_list = random.sample(range(100), 10)
qsort(data_list)
>> [2, 20, 35, 39, 49, 51, 57, 74, 82, 94]
list comprehension으로 좀더 깔끔하게 작성해보기
def qsort(data):
if len(data) <= 1:
return data
pivot = data[0]
left = [item for item in data[1:] if pivot > item]
right = [item for item in data[1:] if pivot <= item]
return qsort(left) + [pivot] + qsort(right)
4. 알고리즘 분석
병합정렬과 유사, 시간복잡도는 O(n log n)
평균적으로 절반씩 나눠져서 비교하므로, 결과적으로 단계가 log n 만큼 생성되고
각 단계별로 n 만큼 피벗과 비교하는데 시간이 걸리므로
일반적인 경우의 시간복잡도는 O(n logn) 이다.
단, 최악의 경우
- 맨 처음 pivot이 가장 크거나, 가장 작으면
- 모든 데이터를 비교하는 상황이 나옴
- O(𝑛^2)

'🕶 Algorithm > 알고리즘' 카테고리의 다른 글
| 순차 탐색 (Sequential search) (0) | 2021.08.06 |
|---|---|
| 병합 정렬 (Merge sort) (0) | 2021.08.06 |
| 동적 계획법 (Dynamic Programming)과 분할 정복 (Divide and Conquer) (0) | 2021.07.23 |
| 재귀 (Recursion) (0) | 2021.07.22 |
| 삽입 정렬 (Insertion sort) (0) | 2021.07.21 |