1. 최대우도법
최대우도법(Maximum Likelihood Estimation, 이하 MLE)은 모수적인 데이터 밀도 추정 방법이다.
다양한 파라미터 으로 구성된
어떤 확률밀도함수 에 대해서 관찰하고
표본 데이터 집합을 이라 할 때,
이 표본들에서 파라미터 를 추정하는 방법이다.
당연히, 이 말만 보면 MLE가 뭔지 이해하기는 불가능하기 때문에 예시를 들어 MLE에 대해 알아보도록 하자.

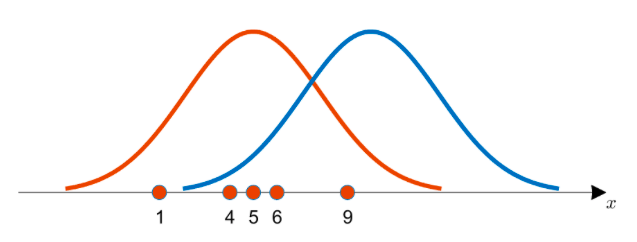
위와 같이 5개의 데이터 {1, 4, 5, 6, 9} 를 얻었다고 하자.
이 데이터를 어떤 분포로 부터 얻었을까? 를 알고 싶다.
주황색 분포, 파란색 분포 중 어떤 데이터에서 얻었을까?
아마 주황색 분포가 좀더 가능성이 있을 것이다.
그럼 이것을 어떻게 수학적으로 정교하게 만들까?
이때 Likelihood에 대해서 생각해보아야 한다.
Likelihood는 가능성이며 가능도이다.

각 후보들{1, 4, 5, 6, 9} 로부터 높이를 계산할 수 있다.
각각의 데이터들이 갖는 확률밀도함수(pdf)를 알 수 있다.
높이 하나 하나를 Likelihood 에 기여하는 기여도 라고 하고,
이 기여도는

로 나타낼 수 있다.
모든 데이터(xk) 로부터 얻는 확률 밀도 값 P(Xk|θ) 를 다 곱해주는 것을 Likelihood로 정의한다.

주황색 도표와 파랑색 도표의 기여도는 분명히 차이가 있을 것이다.
아마 주황색 도표로부터 얻은 기여도 값이 더 높을 것이다.
따라서

이 Likelihood function을 최대화 할 수 있는 θ를 찾는 것이 Maximum likelihood function(최대우도법) 이다.
보통

이렇게 자연로그를 취해서 구한다.
로그에서 곱은 합으로 바뀐다.
이처럼 계산이 더 편해지기 때문이다.
우리는 L(θ|x) 값의 최댓값을 구해주면 된다.
최댓값을 찾는 방법은 편미분이나 미분을 해서 구해주면 된다.

θ 값이 최대가 되는 지점의 θ값(Likelihood)이 아마도? 우리가 얻은 Sample distribution의 평균값이 아닐까? 라고 예측해 볼 수 있다.
다양한 파라미터로 추출되어
이렇게 여러가지의 평균값을 가진 후보들을 살펴보면서
그중에서 가장 큰 θ값(Likelihood)을 가진 θ
'✏️ Mathemathics > Statistics and Probability' 카테고리의 다른 글
| 나이브 베이즈 분류기 (0) | 2021.05.29 |
|---|---|
| 베이즈 정리의 의미 (0) | 2021.05.29 |
| 사전 확률과 사후 확률 (1) | 2021.05.29 |
| 단순 선형 회귀분석 - 회귀계수의 가설검정 (0) | 2020.04.09 |
| 단순 선형 회귀분석 - 회귀계수의 구간추정 (0) | 2020.04.09 |