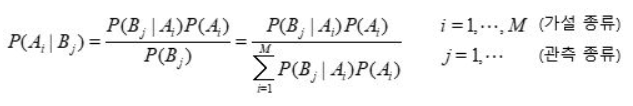
사전 확률 ( Prior Probability )
현재 가지고 있는 정보를 기초로하여 정한 초기 확률
확률 시행 전에 이미 가지고 있는 지식을 통해 부여한 확률
ex) 동전을 던져 앞면이 나올 확률 : 1/2
사후 확률 ( Posteriori Probability)
사건 발생 후에 어떤 원인으로부터 일어난 것이라고 생각되어지는 확률
추가된 정보로부터 사전정보를 새롭게 수정한 확률 ( 수정 확률 )
조건부 확률을 통해 사후 확률을 표현할 수 있음
사후확률은 베이즈 정리로 부터 구할 수 있다.
사후 확률의 계산 => 베이즈 정리
사후확률 P(A|B)을 사전확률 P(A),P(B) 및 조건부확률 P(B|A)로 표현할 수 있음
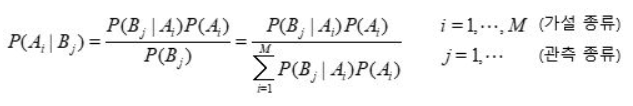
- 여기서 P(Ai|Bj)는 사후확률
B는 관측, A는 원인, 즉, 관측 B를 보고 원인이 A라고 생각되는 확률
- P(Ai)는 원인/소스별 사전확률
- P(Bj|Ai)는 우도(조건부 확률)
각각의 원인 Ai로부터 결과 Bj가 나타날 것이라는 가설에 대해 지지하는 정도 .
- P(Bj)는 해당 결과가 나오도록 모든 원인들 마다 기여하는 확률들의 합
사후확률의 계산에는 필요한 값이나, 추론/결정/판정에 영향을 미치지 않는 정규화된 상수로 취급됨
대개, 원인이 각 결과에 기여하는 정도가 같고, 정적인 경우임
우도 (Likelihood, 가능성/가능도)
우도의 의미
나타난 결과에 따라 여러 가능한 가설들을 평가할 수 있는 측도(Measure)이다.
확률적으로 조건부확률로 표현할 수 있음, 우도는 확률로 표현되나 각 가설에 대한 가능도/지지도 등의 의미가 강하다. 여기서 각 가설에 대한 우도는 그 가설을 지지하는 정도라고 볼 수 있다.
우도의 활용
알려진 결과(관측된 표본)에 기초하여, 미지 모수에 대한 추정(가설)의 정확성에 대한 질적인 평가 척도
우도의 계산
나타난 결과에 해당하는 각 가설 마다 계산해야 하는 값이다.
최대 우도 원리
나타난 결과에 해당하는 각 가설 마다 계산된 우도 값 중 가장 큰 값을 선택하는 것이다.(최대우도추정)
우도의 확률적 표현 = 조건부확률
우도(조건부확률)의 표기 : P(Bj|Ai) - 각각의 원인 Ai으로부터 결과 Bj가 나타날 것이라는 가설에 대해 지지하는 정도 . 나타난 결과 Bj 마다 다른 값을 갖는 여러 가설 Ai 들을 평가할 수 있는 조건부확률 , 각각의 원인 Ai은, 분류 범주/분류 영역/카테고리 라고도 함
'✏️ Mathemathics > Statistics and Probability' 카테고리의 다른 글
| 베이즈 정리의 의미 (0) | 2021.05.29 |
|---|---|
| 최대우도법 (0) | 2021.05.29 |
| 단순 선형 회귀분석 - 회귀계수의 가설검정 (0) | 2020.04.09 |
| 단순 선형 회귀분석 - 회귀계수의 구간추정 (0) | 2020.04.09 |
| 단순 선형 회귀분석 - 회귀식 추정 및 결정계수 (0) | 2020.04.09 |