

점추정 값, 구간추정 값이 있다.
마찬가지로 회귀 식에서도 점추정할 수 있고 구간 추정할 수 있다.
그러려면 분산의 개념을 알아야 한다.
오차가 작으면 구간도 작다.
분산이 작을수록 베타1 베타0의 구간이 작게 나타날 것이다.
상세설명
베타0 베타1 은 파라미터 모수가 된다.
확률변수 yi 가 될수 있는 것은 입실론이다.
입실론은 N(0,분산) 즉 정규분포를 따르고, 따라서 yi가 정규분포를 따른다.
우리는 오차항에 대한 분포를 알아야 yi의 분포도 알 수 있다.
점추정을 할 수 도있고 구간 추정을 할 수도 있다.
오차분산이 작을수록 회귀직선에 더욱 가깝다.
분산이 작을수록 추정하고자하는 베타0와 베타1의 구간도 작게 나타날 것이다.
오차분산은 ^yi와 실제 관측값 yi의 편차를 이용하여 추정한다.
잔차 제곱 합을 sum of squares for eroor 라고 한다.
^yi 은
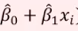
라고 쓰기도 한다.
따라서 (실제값 - 예측값)의 제곱을 SSE 라고 한다.
yi - ^yi = 잔차
이를 위해 다음과 같이 개개의 관측값 yi와 추정값 ^yi의 편차를 다루게 되며 이 편차를 잔차(residual)라고 한다.

그리고 다음과 같이 잔차들의 제곱을 모두 더한 합을 오차제곱합(sum of squares for error; SSE) 라고 한다.

SSE = (실제값 - 예측값)^2


상세 설명
SSE를 minimize하고 싶은데 이때 분산이 있다.
오차분산은 SSE를 n-2로 나눈다.
시그마 헷 제곱 = 추정 분산

상세 설명
기울기는 x,y의 공분산 / x의 편차제곱 이다.
이걸 이용해서 SSE를 더 쉽게 표현할 수 있다.
암기 ****



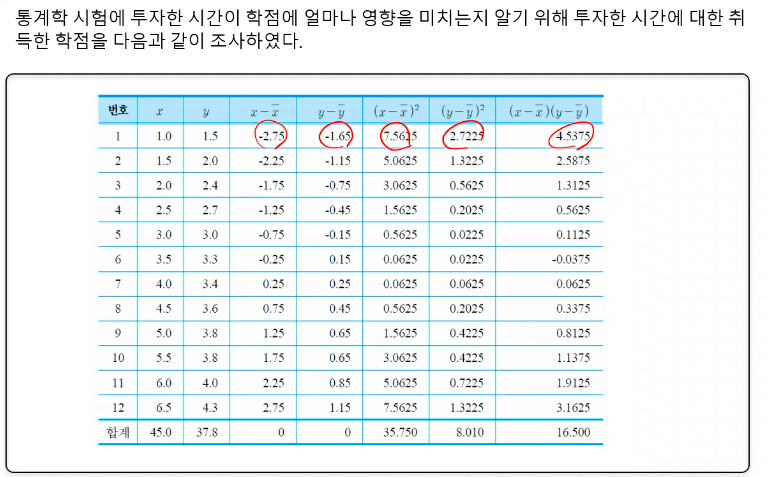
예제 3.

이와 같이 얻은 회귀 모형이 얼마나 잘 설명하는지를 나타내는 방법으로 결정계수(R^2)를 생각할 수 있다.
총 편차중에 회귀식이 설명하는 변동을 뭐라하냐? R^2이라고 한다.
다음 그림과 같이 종속변수 yi와 yi들의 평균 y⌒와의 차이 (yi-y⌒)를 총편차(total deviation)이라 하며, 이와 같은 총편차들의 제곱합을 총제곱합(total sum of squares)이하고 SST라고 나타낸다.
즉, 총제곱합은 다음과 같다.



상세 설명
데이터가 있다면 회귀식이 있다고 생각하지 마라.
평균이 있을것이다 이것은 y바 라고하자
y1, y2, y3와 y바와의 차이의 제곱을 SST 라고 한다.
회귀식이 반영됐나? 반영 안됐다. 데이터 자체가 갖고 있는 총 변동의 양이다.
그렇다면 오차항은 뭔가?
회귀식이 나와있다. 직선
실제값과 예측값의 편차제곱을 SSE (오차항에 의한 설명) 라고 한다.
직선에서 회귀식이 설명하는 변동
전체 변동 중 회귀식이 설명하는 변동 SSR (regressor 에 의한 제곱합)이라고 한다
그러면 각각의 총 편차는 다음과 같이 오차항에 의하여 설명되는 부분 yi-^yi 와 회귀직선에 의해 설명되는 부분인 yi-⌒yi 와의 합으로 표현될 수 있다.

그러면 SST는 다음과 같다.

상세 설명
SST(실제값과 평균의 차) = SSE(실제값과 예측값의 차이) + SSR(회귀식이 전체평균에서 얼만큼 떨어져 있는지) + 0
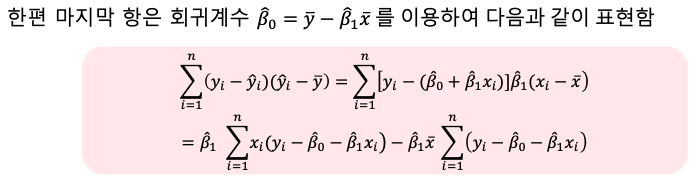
이때 정규방정식을 이용하면 다음을 얻는다.

따라서 SST는 다음과 같다.

SST = SSE + SSR
자료 자체의 총변동 = SST
평균을 중심으로 회귀식을 얼마나 잘 설명하고 있는가 = SSR

따라서 다음과 같이 총제곱합(총변동)은 오차제곱합과 회귀제곱합으로 표현된다.

이때 앞에서 설명한 바와 같이 오차가 작을수록 추정회귀직선은 자료들을 대표하기에 적합하다.
따라서 오차제곱합 SSE가 작을수록(또는 SSR이 커질수록) 회귀모형이 자료들을 잘 설명해준다.
이와같은 회귀모형의 적합도를 나타내는 모수로 다음과 같이 정의되는 결정계수(coefficient of determination)를 사용한다

상세 설명
그렇다면 우리가 말하는 경정계수라는 것은 무엇인가.
회귀모형의 적합도를 의미하는데 그게바로 총 변동중에 회귀식이 설명하는 변동이다.
총 변동 중 회귀식이 몇퍼이냐.
그런데 SSR = SST - SSE 이므로
1 에서 오차가 설명하는 변동을 빼도 된다.
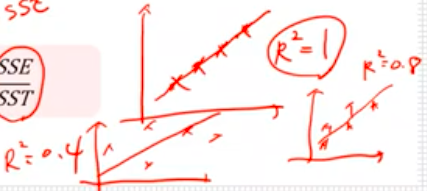
1 에 가까울수록 좋은 값이고 0에 가까울수록 회귀식이 설명을 잘 못한다.
이 결정계수는 회귀직선에 의해 설명되는 종속변수 y에 대한 총 변동의 비율로 0과 1 사이의 값이다.
R^2이 클수록 SSE가 작아지며, R^2 = 1이면 회귀모형은 완전하다고 한다.
반면에 SSE가 SST에 가까울수록 R^2이 0에 가까워지고, 이 경우에 회귀모형은 매우 나쁘다.




전체 변화량의 88.7%는 회귀식이 설명하고있다.
11.3%는 오차가 설명하고 있다.




'✏️ Mathemathics > Statistics and Probability' 카테고리의 다른 글
| 단순 선형 회귀분석 - 회귀계수의 가설검정 (0) | 2020.04.09 |
|---|---|
| 단순 선형 회귀분석 - 회귀계수의 구간추정 (0) | 2020.04.09 |
| 3주차 과제 (0) | 2020.04.02 |
| 최소 제곱법 (0) | 2020.03.25 |
| p-value (0) | 2020.03.23 |