비볼록 함수
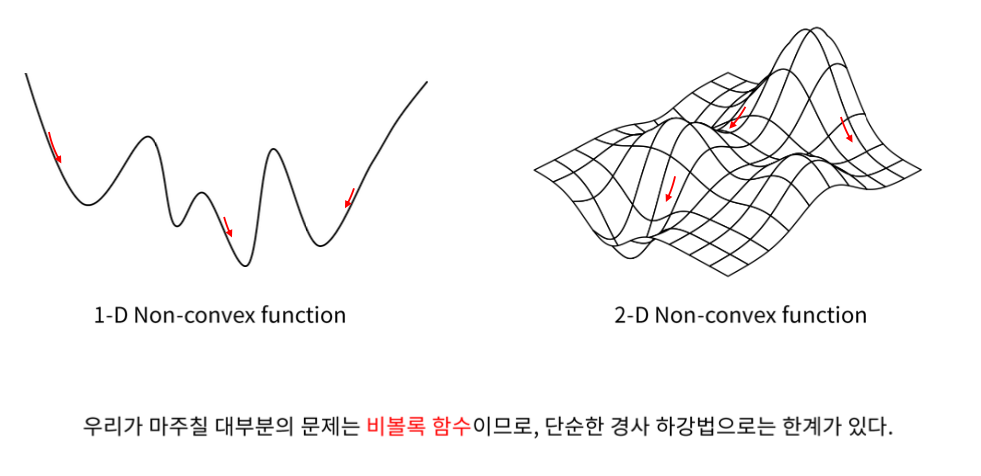
지역 최솟값 (Local minimum)

안장점 (Saddle point)

한쪽으로는 최댓값, 다른 쪽으로는 최솟값을 띄는 곳
전반적으로 봤을 때 최댓값도 최솟값도 아니게 되는 지점이 된다.
기울기가 0이 되지만 극값이 아니다.
경사하강법의 여러가지 접근 방법
1. 관성 (Momentum)

관성을 이용해서 계속해서 내려갈 수 있는 힘을 갖게 한다.
vt = t-1 번째와 t 번째 사이에 있는 이동벡터
vt는 학습률 x 기울기에 이전 속도에 관성계수를 곱해서 더해준 것 밖에 없다.
2. 적응적 기울기 (AdaGrad)

Adaptive gradient는 변수별로 학습률이 달라지게 하는 방법이다.
기존의 gradient descent에 해당하는 부분은 -η·▽f(xt-1)이다.
이 부분에 1/루트 gt + ε 이 추가가 되었다.
계속해서 무언가를 누적해서 더해가는데
그 내용은 ▽f(xt-1)의 제곱이다.
한번 계산 될때마다 각각의 스칼라를 더해준다.
음수던 양수던 크기를 표현하게 되는 것을 누적해서 더해주는 것이다.
그러면 gradient에 비례해서 현재까지 얼만큼 gradient에 의해서 이동을 했는지,
각각의 변수들에 따라서 계산해주는 꼴이 된다.
따라서 gt가 크면 클수록 학습이 많이 된 변수이다.
제곱을 했기 때문에 루트를 취해준다.
ε 이 붙는 이유는 gt가 0에 가까우면 무한대에 튀기 때문에 분모가 0이 되지 않게끔 해준다.
결국 gradient의 크기로 나눠줌으로써 학습이 많이 된 것을 gradient값을 나눠서 줄여주는 효과가 있다.
RMSProp

람다라는 상수만큼 감쇠가 이루어지기 때문에 gt가 무한정 커져서 학습이 잘 안되게끔 하는 것을 막는다.
따라서 RMS Prop은 학습을 오랫동안 진행할 수 있는 장점이 있다.
Adam

'💡 AI > DL' 카테고리의 다른 글
| DNN의 수학적 이해 (1) | 2021.02.01 |
|---|---|
| Deep Neural Network - Back Propagation (0) | 2021.02.01 |
| 경사하강법의 수학적 표현 (0) | 2021.01.31 |
| 최적화 이론의 수학적 표현 (0) | 2021.01.28 |
| Gradient Descent 란? (0) | 2021.01.28 |