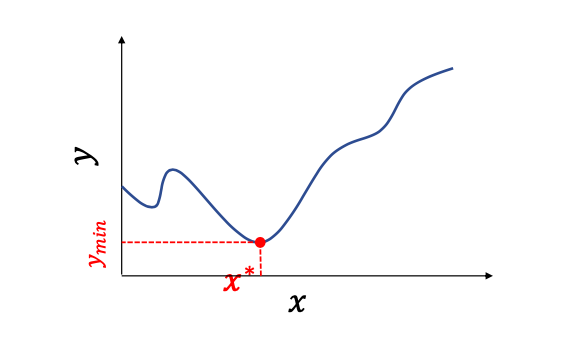
최적화 이론의 수학적 표현

개념은 이해했으니 이제 수학적으로 어떻게 표현하는지 알아보자.
최적화 이론 (Optimization Theory)

f(x)라는 함수가 주어진다.
이 함수는 Loss function이다.
우리는 이것을 minimize 해야한다.
가장 작게 하는 x값이 중요하다.
g(x)와 h(x)는 제약 조건이다.
몇개라도 제약을 줄 수 있고 어떻게 제약을 주냐에 따라서 최적화 문제를 어떻게 풀 것인가가 달라지게 된다.
제약 조건에 맞는 x들 중에서 최적해(f(x)의 최소값)를 찾는다.
최소화 문제나 최대화 문제는 사실 동일한 문제이다. 왜냐하면 - 만 붙이면 되기 때문이다.
딥러닝에서는 제약조건을 사용하지 않는다.
Analytical method vs Numerical method
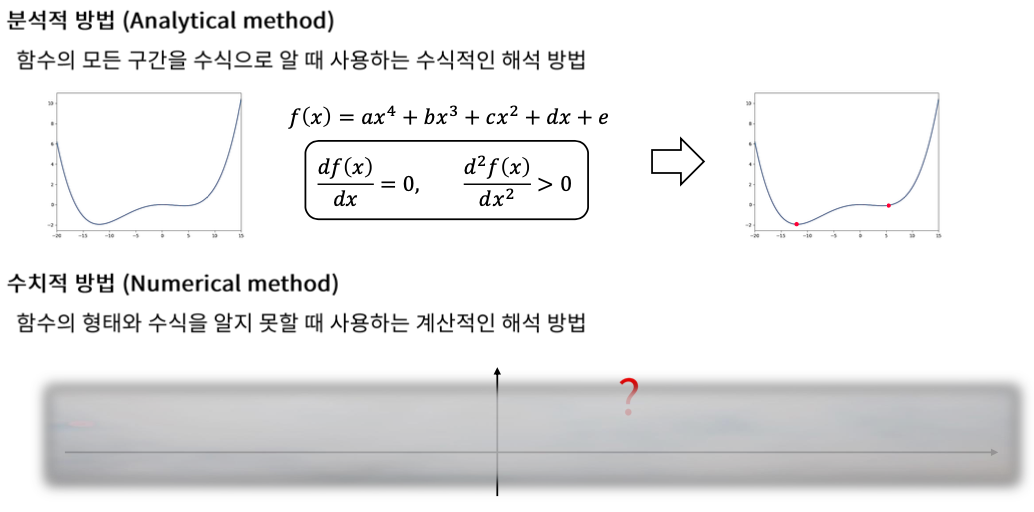
최적화 문제를 푸는 방법은 크게 2가지가 있다.
분석적 방법과 수치적 방법이다.
Analytical method
분석적 방법은 수식적으로 푸는 방법이다.
어떤 함수가 4차식이라는 것을 알고 있을 때, 이것을 2번 미분하여 0보다 크다면 최솟값이 된다는 것을 알 수 있다.
Numerical method
수치적 방법은 수식이 어떻게 되는지 함수가 어떻게 되는지 모를 때 쓰는 방법이다.
가장 대표적인 것이 경사하강법이다.
Global solution vs Local solution

딥러닝과 최적화 이론

Training input을 넣어서 나온 Training output과 Label을 Loss function을 이용해서 비교를 하고
Error값을 최소화 하도록 Alogorithm Optimizer를 이용해서 (Numerical method를 이용해서)
Network Architecture에 있는 Trainable parameter를 최적화 하는 것이 딥러닝과 최적화이론의 연결 관계이다.
'💡 AI > DL' 카테고리의 다른 글
| 심화 경사하강법 (0) | 2021.01.31 |
|---|---|
| 경사하강법의 수학적 표현 (0) | 2021.01.31 |
| Gradient Descent 란? (0) | 2021.01.28 |
| Supervised Learning, Unsupervised Learning, Loss function (0) | 2021.01.28 |
| SNN을 이용한 Multi-Class Classification (0) | 2021.01.27 |