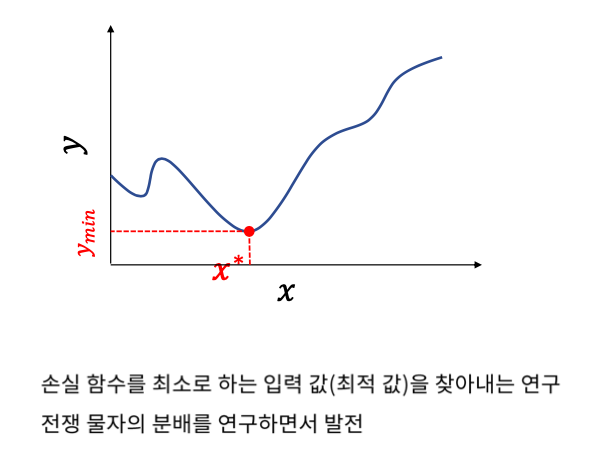
최적화 이론

최적화 이론은 함수의 출력이 최대나 최소가 되게하는 입력값을 찾는 것이라고 하였다.
무차별 대입법 (Brute-Force)

Brute Force는 최적화 방법의 가장 단순한 방법이다.
실제로 사용할 수는 없다.
범위를 알아야 하기 때문에 아무리 다 대입해봐야 찾지 못할 수도 있다.
주변에 더 작은 f(x)의 값이 있을 수 있기 때문에 무한하게 조사해야 한다.
따라서 계산복잡도가 매우 높다.
이것을 알고리즘이라고 하기엔 어렵다.
경사하강법 (Gradient Descent)

Gradient는 기울기를 의미한다.
경사를 따라서 여러번 스텝을 밟아 최적점으로 다가가는 것을 경사하강법이라고 한다.
랜덤한 시작점에서 미분을 하게되면 하나의 기울기를 얻게 된다.
그러면 어느 방향으로 가야 더 내려가는지 알 수 있다.
계속 반복하며 최적값을 얻을 수 있다.
학습률의 선택 (Learning Rate)

미분 값을 가지고 이동할 때 기울기 값에 α를 곱해서 이동하게 된다.
학습률에 비례해서 이동하기 때문에, 학습률에 따라서 학습이 어떻게 될지 결정된다.
α가 작은 경우에는 접근을 느리게 해서 굉장히 느리게 최적값에 도달한다.
α가 큰 경우에는 널뛰어 버리는 문제가 있다. 이 또한 잘 접근하지 못하고 진동하는 것처럼 보이는 현상이 나타난다.
따라서 적절한 학습률을 선택하는 것이 중요하다.
볼록 함수 (Convex Function)

볼록 함수의 경우에는 경사하강법을 이용해서 최적 값에 도달할 수 있다.
비볼록 함수 (Non-convex Function)

어디서 시작하느냐에 따라서 다른 최적값을 가지게 된다.
여러가지 극값이 나타나며 이것을 Local Minimum이라고 한다.
'💡 AI > DL' 카테고리의 다른 글
| 경사하강법의 수학적 표현 (0) | 2021.01.31 |
|---|---|
| 최적화 이론의 수학적 표현 (0) | 2021.01.28 |
| Supervised Learning, Unsupervised Learning, Loss function (0) | 2021.01.28 |
| SNN을 이용한 Multi-Class Classification (0) | 2021.01.27 |
| SNN을 이용한 Classification, Sigmoid function (0) | 2021.01.27 |