목차
- 알고 있는 metric에 대해 설명해주세요. (ex. RMSE, MAE, recall, precision ...)
- 정규화를 왜 해야할까요? 정규화의 방법은 무엇이 있나요?
- Local Minima와 Global Minima에 대해 설명해주세요.
- 차원의 저주에 대해 설명해주세요.
- Dimension reduction 기법으로 보통 어떤 것들이 있나요?
- PCA는 차원 축소 기법이면서, 데이터 압출 기법이기도 하고, 노이즈 제거 기법이기도 합니다. 왜 그런지 설명 해주실 수 있나요?
- PCA, LSA, LDA, SVD 등의 약자들이 어떤 뜻이고 서로 어떤 관계를 가지는지 설명할 수 있나요?
- Markov Chain을 고등학생에게 설명하려면 어떤 방식이 제일 좋을까요?
- SVM은 왜 반대로 차원을 확장시키는 방식으로 동작할까요? 그리고 SVM은 왜 좋을까요?
알고 있는 metric에 대해 설명해주세요. (ex. RMSE, MAE, recall, precision ...)
평가지표(metric)을 크게 분류를 위한 평가지표와 회귀를 위한 평가지표로 나눌 수 있다.
우선 분류 작업(task)에 적용할 수 있는 평가지표를 살펴보자.
정확도(Accuracy)
정확도는 모델의 예측이 얼마나 정확한지를 의미한다. 정확도는 (예측 결과가 동일한 데이터 개수)/(전체 예측 데이터 개수)로 계산할 수 있다. 하지만 라벨 불균형이 있는 데이터에서 정확도를 사용하면 안 된다. 예를 들면, 0과 1의 비율이 9:1인 데이터가 있다고 했을 때, 모두 0으로 예측하면 정확도가 90%가 나올 것이다. 이는 잘못된 판단이므로 정확한 판단을 위해서는 다른 지표를 사용해야 한다.
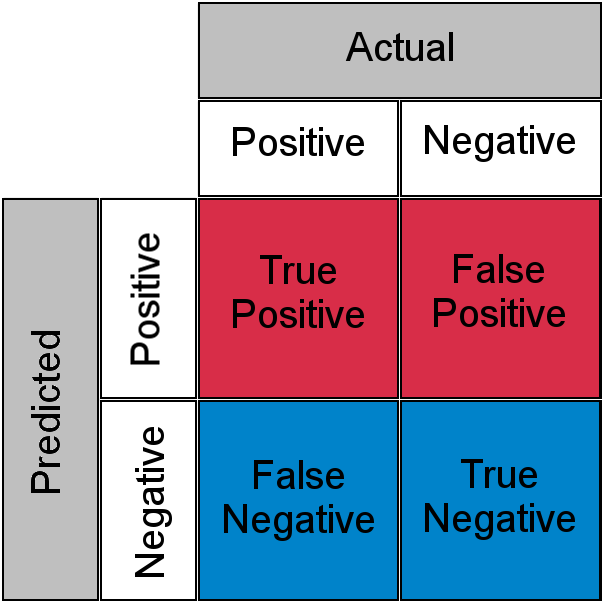
오차 행렬(confusion matrix)

오차 행렬은 모델이 예측을 하면서 얼마나 헷갈리고 있는지를 보여주는 지표이다. 주로 이진 분류에서 많이 사용하며 이진 분류에 대한 오차 행렬은 위의 그림처럼 같이 나타낼 수 있다. True Positive는 긍정으로 예측을 했는데 실제로 긍정인 경우를, False Positive는 긍정으로 예측했는데 실제로 부정인 경우를, False Negative는 부정으로 예측했는데 실제로 긍정인 경우를, True Negative는 부정으로 예측했는데 실제로 부정인 경우를 말한다. 위의 값을 바탕으로 모델이 어떤 오류를 발생시켰는지를 살펴볼 수 있다.
참고로 정확도는 (TN + TP) / (TN + FP + FN + TP)로 계산할 수 있다.
정밀도(precision), 재현율(recall)
정밀도와 재현율은 긍정 데이터 예측 성능에 초점을 맞춘 평가지표이다.
정밀도란 예측을 긍정으로 한 데이터 중 실제로 긍정인 비율을 말하며, 재현율은 실제로 긍정인 데이터 중 긍정으로 예측한 비율을 말한다. 오차 행렬을 기준으로 정밀도는 TP / (FP + TP)으로, 재현율은 TP / (FN + TP)으로 계산할 수 있다.
정밀도와 재현율은 트레이드오프 관계를 갖는다. 정밀도는 FP를, 재현율은 FN을 낮춤으로써 긍정 예측의 성능을 높인다. 이 같은 특성 때문에 정밀도가 높아지면 재현율은 낮아지고 재현율이 높아지면 정밀도는 낮아진다. 가장 좋은 경우는 두 지표 다 적절히 높은 경우이다.
F1-Score
정밀도와 재현율 한 쪽에 치우치지 않고 둘 다 균형을 이루는 것을 나타낸 것이 F1-Score이다. F1-Score는 정밀도와 재현율의 조화평균으로 계산할 수 있다.
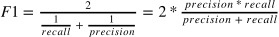
ROC-AUC
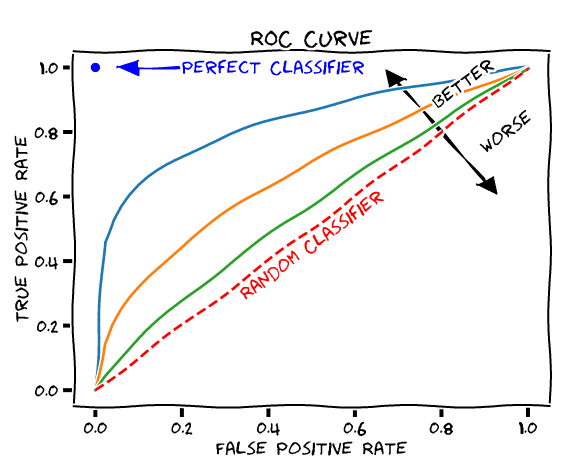
ROC는 FPR(False Positive Rate)가 변할 때 TPR(True Positive Rate)가 어떻게 변하는지를 나타내는 곡선을 말한다. 여기서 FPR이란 FP / (FP + TN)이고, TPR은 TP / (FN + TP)으로 재현율을 말한다. 그럼 어떻게 FPR을 움직일까? 바로 분류 결정 임계값을 변경함으로써 움직일 수 있다. FPR이 0이 되려면 임계값을 1로 설정하면 된다. 그럼 긍정의 기준이 높으니 모두 부정으로 예측될 것이다. 반대로 1이 되려면 임계값을 0으로 설정하여 모두 긍정으로 예측시키면 된다. 이렇게 임계값을 움직이면서 나오는 FPR과 TPR을 각각 x와 y 좌표로 두고 그린 곡선이 ROC이다.
AUC는 ROC 곡선의 넓이를 말한다. AUC가 높을수록 즉, AUC가 왼쪽 위로 휘어질수록 좋은 성능이 나온다고 판단한다. 즉, TPR이 높고 FPR이 낮을수록 예측 오류는 낮아지기 때문에 성능이 잘 나온다 볼 수 있다.
다음으로 회귀 작업에 적용할 수 있는 평가지표를 살펴보자.
MAE(Mean Absolute Error)는 예측값과 정답값 사이의 차이의 절대값의 평균을 말한다.
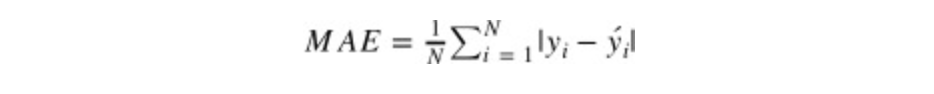
MSE(Mean Squared Error)는 예측값과 정답값 사이의 차이의 제곱의 평균을 말하며, MAE와 달리 제곱을 했기 때문에 이상치에 민감하다.
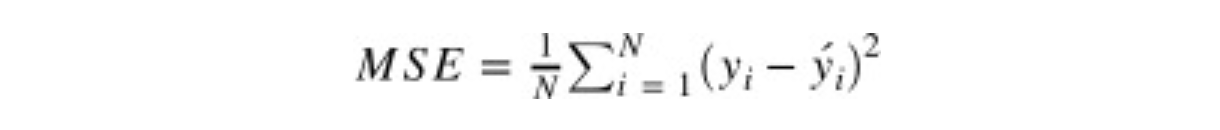
RMSE(Root Mean Squared Error)는 MSE에 루트를 씌운 값을 말한다.
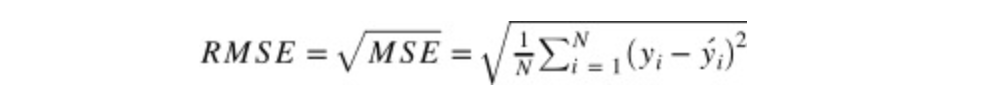
RMSLE(Root Mean Squared Logarithmic Error)는 RMSE와 비슷하나 예측값과 정답값에 각각 로그를 씌워 계산을 한다.
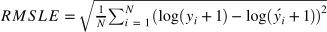
R Squared는 분산을 기반으로 예측 성능을 평가하는 지표를 말한다. 정답값의 분산 대비 예측값의 분산 비율을 지표로 하며, 1에 가까울수록 정확도가 높다.
2. 정규화를 왜 해야할까요? 정규화의 방법은 무엇이 있나요?
정규화는 개별 피처의 크기를 모두 똑같은 단위로 변경하는 것을 말한다. 정규화를 하는 이유는 피처의 스케일이 심하게 차이가 나는 경우 값이 큰 피처가 더 중요하게 여겨질 수 있기 때문이다. 이를 막기 위해 피처 모두 동일한 스케일로 반영되도록 하는 것이 정규화이다.
정규화하는 방법으로는 대표적으로 두 가지가 존재한다.
첫 번째 정규화 방법은 최소-최대 정규화(min-max normalization)으로 각 피처의 최소값을 0, 최대값을 1로 두고 변환하는 방법이다. 값을 x로, 최소값을 min, 최대값을 max로 둘 때, 정규화된 값은 (x-min) / (max-min)으로 계산할 수 있다.
두 번째 정규화 방법으로 Z-점수 정규화(z-score normalization)이 있다. 이 방법은 각 피처의 표준편차와 평균으로 값을 정규화시킨다. 정규화된 값은 (x-mean) / std 로 계산할 수 있다.
3. Local Minima와 Global Minima에 대해 설명해주세요.
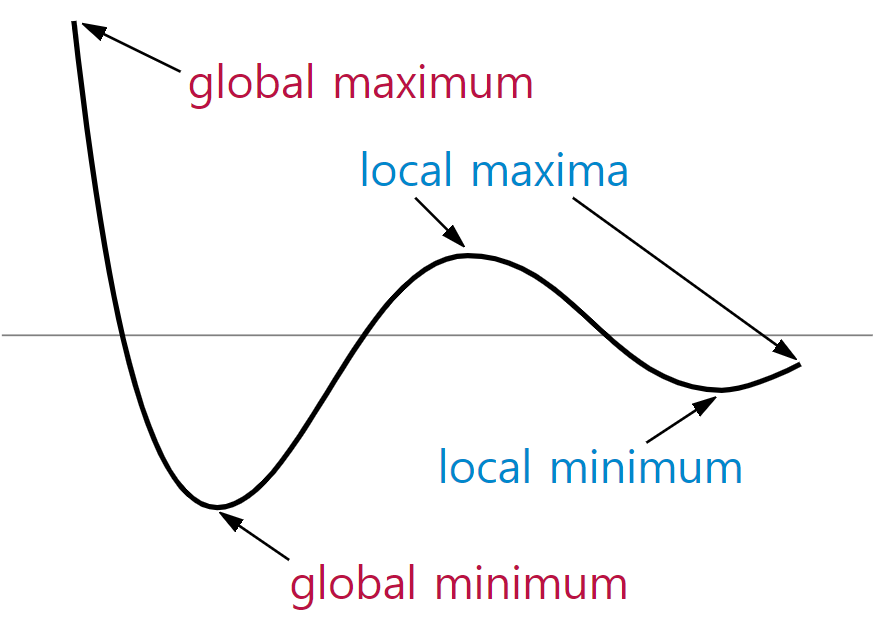
비용 함수(cost function)에서의 Global Minima는 에러가 최소화되는, 즉, 우리가 찾고자 하는 지점을 말하며, Local Minima는 에러가 최소가 될 수 있는 후보가 되는 지점 중 Global Minima를 뺀 지점을 말한다. Local Minima는 자칫 에러가 최소화되는 지점을 찾았다고 착각할 수 있기에 함정에 비유할 수 있다. 이를 해결하기 위해 Momentum과 같은 최적화 알고리즘(Activation function)을 사용하거나 학습률(learning rate)를 잘 조절하여 Local Minima에서 벗어날 수 있다.
4. 차원의 저주에 대해 설명해주세요.
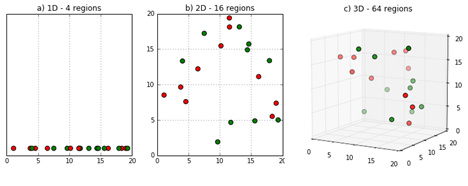
차원의 저주란 데이터 차원이 증가할수록 해당 공간의 크기가 기하급수적으로 증가하여 데이터 간 거리가 기하급수적으로 멀어지고 희소한 구조를 갖게 되는 현상을 말한다. 이를 해결하기 위해서는 차원을 증가시킨만큼 더 많은 데이터를 추가하거나 PCA, LDA, LLE, MDS와 같은 차원 축소 알고리즘으로 차원을 줄여 해결할 수 있다.
5. Dimension reduction 기법으로 보통 어떤 것들이 있나요?
차원 축소는 피처 선택(feature selection)과 피처 추출(feature extraction)으로 나눌 수 있다. 우선 피처 선택은 특정 피처에 종속성이 강한 불필요한 피처는 제거하고 데이터의 특징을 잘 표현하는 주요 피처만 선택하는 것을 말한다. 반면 피처 추출은 기존 피처를 저차원의 피처로 압축하여, 피처를 함축적으로 잘 설명할 수 있도록 저차원으로 매핑하는 것을 말한다. 대표적인 피처 추출 알고리즘으로 PCA, SVD, NMF, LDA 등이 있다.
6. PCA는 차원 축소 기법이면서, 데이터 압축 기법이기도 하고, 노이즈 제거 기법이기도 합니다. 왜 그런지 설명 해주실 수 있나요?
PCA(Principle Component Analysis)는 입력 데이터의 공분산 행렬을 기반으로 고유벡터를 생성하고, 이렇게 구한 고유 벡터에 입력 데이터를 선형 변환하여 차원을 축소하는 방법이다. 차원은 곧 입력 데이터의 피처를 뜻하므로 데이터 압축 기법으로 볼 수도 있다.
또한 PCA는 고유값이 가장 큰, 즉 데이터의 분산이 가장 큰 순으로 주성분 벡터를 추출하는데, 가장 나중에 뽑힌 벡터보다 가장 먼저 뽑힌 벡터가 데이터를 더 잘 설명할 수 있기 때문에 노이즈 제거 기법이라고도 불린다.
7. PCA, LSA, LDA, SVD 등의 약자들이 어떤 뜻이고 서로 어떤 관계를 가지는지 설명할 수 있나요?
PCA는 Principle Component Analysis의 약자로 데이터의 공분산 행렬을 기반으로 고유 벡터를 생성하고 이렇게 구한 고유 벡터에 입력 데이터를 선형 변환하여 차원을 축소하는 방법이다.
SVD는 Singular Value Decomposition의 약자로 PCA와 유사한 행렬 분해 기법을 사용하나 정방 행렬(square matrix)를 분해하는 PCA와 달리 행과 열의 크기가 다른 행렬에도 적용할 수 있다.
LSA는 Latent Semantic Analysis의 약자로 잠재 의미 분석을 말하며, 주로 토픽 모델링에 자주 사용되는 기법이다. LSA는 DTM(Document-Term Matrix)이나 TF-IDF(Term Frequency-Invers Document Frequency) 행렬에 Truncated SVD를 적용하여 차원을 축소시키고, 단어들의 잠재적인 의미를 이끌어낸다. Truncated SVD는 SVD와 똑같으나 상위 n개의 특이값만 사용하는 축소 방법이다. 이 방법을 쓸 경우 원행렬로 복원할 수 없다.
LDA는 Latent Dirichlet Allocation 혹은 Linear Discriminant Analysis의 약자이다. 전자는 토픽모델링에 사용되는 기법 중 하나로 LSA와는 달리 단어가 특정 토픽에 존재할 확률과 특정 토픽이 존재할 확률을 결합확률로 추정하여 토픽을 추정하는 기법을 말한다. 후자는 차원축소기법 중 하나로 분류하기 쉽도록 클래스간 분산을 최대화하고 클래스 내부의 분산은 최소화하는 방식을 말한다.
8. Markov Chain을 고등학생에게 설명하려면 어떤 방식이 제일 좋을까요?
마코프 체인(Markov Chain)
마코프 성질(Markov Property)을 지닌 이산 확률 과정(Discrete-time Stochastic Pross)
마코프 성질(Markov Propery)
n+1회의 상태(state)는 오직 n회에서의 상태, 혹은 그 이전 일정 기간의 상태에만 영향을 받는 것을 의미한다. 예를 들면 동전 던지기는 독립시행이기 때문에 n번째의 상태가 앞이던지 뒤이던지 간에 n+1 상태에 영향을 주지 않는다. 하지만 1차 마코프 체인은 n번째 상태가 n+1번째 상태를 결정하는데에 영향을 미친다. (시간 t에서의 관측은 단지 최근 r개의 관측에만 의존한다는 가정을 하고 그 가정하에 설립)
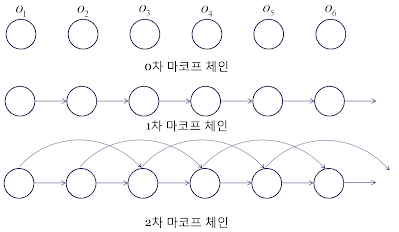
정리하면 마코프 체인은 확률변수(random variable)가 어떤 상태(state)에 도달할 확률이 오직 바로 이전 시점의 상태(state)에 달려 있는 경우를 가리킨다.
예를 들어 오늘의 날씨가 어제의 날씨에만 의존하면 1차 마코프 체인, 이틀 전까지의 날씨에만 의존하면 2차 마코프 체인이다.
마코프 모델
마코프 모델은 위의 가정하에 확률적 모델을 만든 것으로써, 가장 먼저 각 상태를 정의하게 된다. 상태는 V = v1, v2, ... vm 으로 정의하고, m개의 상태가 존재하게 되는 것이다. 그 다음은 상태 전이 확률(State trainsition Probability)을 정의할 수 있다. 상태 전이 확률이란 각 상태에서 각 상태로 이동할 확률을 말한다. 상태 전이 확률 aij는 상태 vi 에서 상태 vj로 이동할 확률을 의미한다.
아래의 식은 상태 전이 확률을 식으로 나타낸 것과 그 아래는 확률의 기본 정의에 의한 상태 전이 확률의 조건이다.
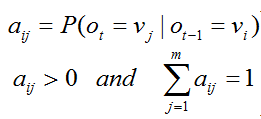
그리고 상태와 상태 전이 확률을 정리하여 상태 전이도(state trainsition diagram)으로도 표현할 수 있다.

9. SVM은 왜 반대로 차원을 확장시키는 방식으로 동작할까요? SVM은 왜 좋을까요?
SVM (Support Vector Machine)
SVM은 데이터가 사상된 공간에서 경계로 표현되며, 공간상에 존재하는 여러 경계 중 가장 큰 폭을 가진 경계를 찾는다.
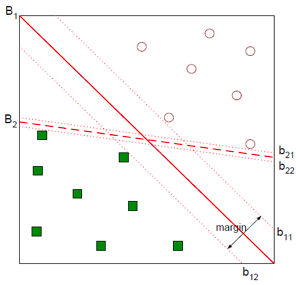
- B1 : 결정 경계
- b11 : plus-plane
- b12 : minus-plane
Margin
Margin은 plus-plane과 minus-plane 사이의 거리를 의미하며, 최적의 결정 경계는 margin을 최대화한다.
SVM은 선형 분류뿐만 아니라 비선형 분류에도 사용되는데, 비선형 분류에서는 입력자료를 다차원 공간상으로 맵핑할 때 커널 트릭(kernel trick)을 사용하기도 한다.
원 공간(Input Space)의 데이터를 선형분류가 가능한 고차원 공간(Feature Space)으로 매핑한 뒤, 두 범주를 분류하는 초평면을 찾는다. (Kernel-SVM)

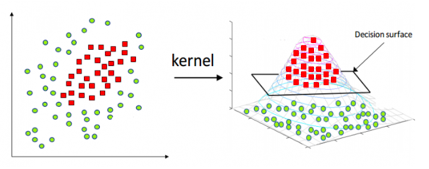
커널 트릭 (Kernel trick)
커널 함수를 이용하여 저차원 공간(low dimensional space)을 고차원 공간(high dimensional space)으로 맵핑해주는 작업
커널 함수의 종류

SVM의 장단점
| 장점 | 단점 |
| 분류와 회귀에 모두 사용할 수 있다. | 데이터 전처리와 매개변수 설정에 따라 정확도가 달라질 수 있다. |
| 신경망 기법에 비해 과적합 정도가 낮다. | 예측이 어떻게 이루어지는지에 대한 이해와 모델에 대한 해석이 어렵다. |
| 예측의 정확도가 높다. | 대용량 데이터에 대한 모델 구축 시 속도가 느리며,메모리 할당량이 크다. |
| 저차원과 고차원 데이터에 대해서 모두 잘 작동한다. |
Ref : https://github.com/SunWooChan/ai-tech-interview/blob/main/answers/2-machine-learning.md#1
'💡 AI > ML' 카테고리의 다른 글
| ML - Ensemble Learning (0) | 2021.11.22 |
|---|---|
| ML - Decision Tree (0) | 2021.11.21 |
| ML - F1 score, ROC-AUC (0) | 2021.11.19 |
| ML - Confusion Matrix, Precision, Recall (0) | 2021.11.18 |
| ML - 평가(evaluation) (0) | 2021.11.12 |