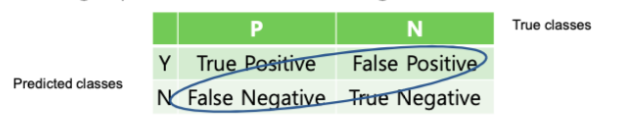
1. Confusion Matrix (오차 행렬)

오차행렬은 이진 분류의 예측 오류가 얼마인지, 어떤 유형의 예측 오류가 발생하고 있는지를 나타내는 지표이다.
예측결과, 예측
True Positive : 참으로 예측했는데, 실제로도 참일 때 = 맞음
False Positive : 참으로 예측했는데, 실제로는 거짓일 때 = 틀림
False Negative : 거짓으로 예측했는데, 실제로는 참일 때 = 틀림
True Negative : 거짓으로 예측했는데, 실제로도 거짓일 때 = 맞음
오차행렬로 예측 결과를 살펴보자.
from sklearn.metrics import confusion_matrix
# 앞절의 예측 결과인 fakepred와 실제 결과인 y_test의 Confusion Matrix출력
confusion_matrix(y_test , fakepred)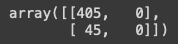
[[TN, FN]
[FP, TP]]
실제 값과 앞에서 예측한 값을 넣으면 위와 같이 나온다.
Negative로 예측했기 때문에 정확도가 90%가 나오는 것이다.
1~10 중에서 7이 아닐것이다 라고 예측했는데 대부분 7이므로 정확도가 높게 나오는 것이다.
그렇기 때문에 정확도를 불균일한 데이터셋을 이진분류할 때 쓰면 안된다.
2. 정밀도(Precision)와 재현율(Recall)
2.1. 정밀도 (Precision)
- TP / (FP + TP)
- 참으로 예측한 것 중에 예측한 것이 맞았을 비율
- FP가 낮아져야 한다.
- "참이라고 예측한 것이 틀리면 안된다" 가 정밀도를 높이는 주된 목표
2.2. 재현율 (Recall)
- TP / (FN + TP)
- 실제 값이 참인 것 중에서 참으로 예측한 것의 비율
- FN이 낮아져야 한다.
- "거짓이라고 예측한 것이 틀리면 안된다" 가 재현율을 높이는 주된 목표
정밀도는 precision_score()
재현율은 recall_score()
from sklearn.metrics import accuracy_score, precision_score , recall_score
print("정밀도:", precision_score(y_test, fakepred))
print("재현율:", recall_score(y_test, fakepred))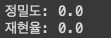
둘다 0으로 나온다.
참으로 예측한게 맞은게 하나도 없기 때문이다.
한마디로 모델이 쓰레기라는 것이다.
오차행렬, 정밀도, 재현율 다 구하는 함수 만들기
from sklearn.metrics import accuracy_score, precision_score , recall_score , confusion_matrix
def get_clf_eval(y_test , pred):
confusion = confusion_matrix( y_test, pred)
accuracy = accuracy_score(y_test , pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
print('오차 행렬')
print(confusion)
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}'.format(accuracy , precision ,recall))
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# 원본 데이터를 재로딩, 데이터 가공, 학습데이터/테스트 데이터 분할.
titanic_df = pd.read_csv('./titanic_train.csv')
y_titanic_df = titanic_df['Survived']
X_titanic_df= titanic_df.drop('Survived', axis=1)
X_titanic_df = transform_features(X_titanic_df)
X_train, X_test, y_train, y_test = train_test_split(X_titanic_df, y_titanic_df, test_size=0.20, random_state=11)
lr_clf = LogisticRegression()
lr_clf.fit(X_train , y_train)
pred = lr_clf.predict(X_test)
get_clf_eval(y_test , pred)
2.3. 업무에 따른 재현율과 정밀도의 상대적 중요도
재현율(Recall)이 중요한 경우
- 실제로 참인 것을 거짓으로 예측하면 큰일 나는 경우
- 거짓인 것을 중점적으로 찾을 때
- 거짓으로 예측한게 틀리면 안된다.
- ex) 암진단
정밀도(Precision)가 중요한 경우
- 실제로 거짓인 것을 참으로 예측하면 큰일 나는 경우
- 참인 것을 중점적으로 찾을 때
- 참이라고 예측한게 틀리면 안된다.
- ex) 스팸 메일
Trade-off
정밀도나 재현율 중 둘중 하나가 좋아야 될 경우, Theshold 를 조정함으로써 성능 수치를 높일 수 있다.
그러나 서로 상호 보완적이기 때문에 한쪽을 의도적으로 높이면 반대쪽은 낮아지게 된다. 이런 것을 Trade-off 라고 부른다.
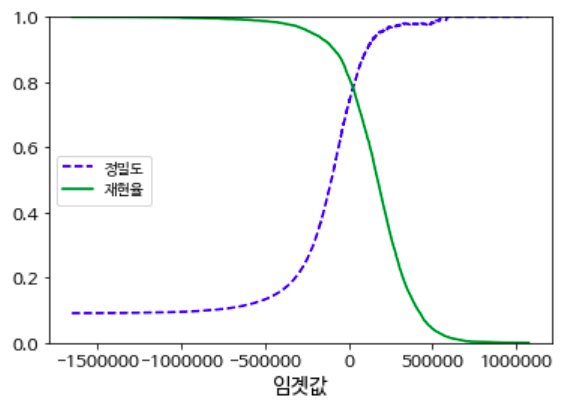
재현율 측면에서 보았을 때, (FN)
- Threshold를 낮춘다는 것은 거짓으로 예측할 확률을 낮추는 것이다.
- 즉, 암이 아니라고 판단할 확률을 낮춘다는 것이다.
- Threshold가 낮아질수록 재현율이 증가한다.
- FN값(거짓으로 예측한 것 중에 틀린 것)이 작아진다.
반면에 정밀도 측면에서 보았을 때, (FP)
- Threshold를 낮춘다는 것은 참으로 예측할 확률을 높이는 것이다.
- 즉, 암이 맞다라고 판단할 확률을 높인다는 것이다.
- Threshold가 낮아졌기 때문에 틀릴 확률도 높아진다.
- FP(참이라고 예측한 것 중에서 틀린 것)값은 높아진다.
그래서 Threshold를 낮추면 재현율은 증가한다.
사이킷런 Estimator 객체의 predict_proba() 는 분류 결정 예측 확률을 반환한다.
사이킷런의 precision_recall_curve() 는 임계값에 따른 정밀도, 재현율의 변화값을 제공한다.
3. predict_proba()
pred_proba = lr_clf.predict_proba(X_test)
pred = lr_clf.predict(X_test)
print('pred_proba()결과 Shape : {0}'.format(pred_proba.shape))
print()
print('pred_proba array에서 앞 3개만 샘플로 추출 \n:', pred_proba[:3])
print()
# 예측 확률 array 와 예측 결과값 array 를 concatenate 하여 예측 확률과 결과값을 한눈에 확인
pred_proba_result = np.concatenate([pred_proba , pred.reshape(-1,1)],axis=1)
print('두개의 class 중에서 더 큰 확률을 클래스 값으로 예측 \n',pred_proba_result[:3])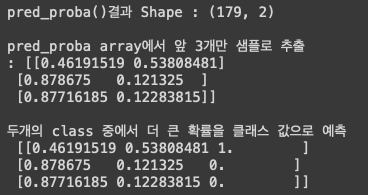
[0이될 확률, 1이될 확률] 순으로 나온다.
3.1. Binarizer 활용
Binarizer는 threshold 기준값 보다 같거나 작으면 0을, 크면 1을 반환해준다.
from sklearn.preprocessing import Binarizer
X = [[ 1, -1, 2],
[ 2, 0, 0],
[ 0, 1.1, 1.2]]
# threshold 기준값보다 같거나 작으면 0을, 크면 1을 반환
binarizer = Binarizer(threshold=1.1)
print(binarizer.fit_transform(X))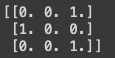
1.1 보다 작은 것은 다 0을 반환, 큰 것은 다 1을 반환하는 것을 볼 수 있다.
3.2. 분류 Threshold 0.5 에서 Binarizer를 이용하여 예측값 반환
from sklearn.preprocessing import Binarizer
#Binarizer의 threshold 설정값. 분류 결정 임곗값임.
custom_threshold = 0.5
# predict_proba( ) 반환값의 두번째 컬럼 , 즉 Positive 클래스 컬럼 하나만 추출하여 Binarizer를 적용
pred_proba_1 = pred_proba[:,1].reshape(-1,1)
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)
get_clf_eval(y_test, custom_predict)
일반적으로 predict()가 0이냐 1이냐를 판단하는 디폴트 threshold 값은 0.5이다.
pred_proba의 두번째 컬럼인 positive만 추출해서 2차원으로 만든다. Binarizer에 들어가는 값은 2차원이 되어야 하기 때문.
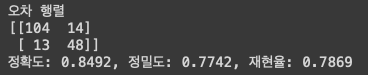
위에서 오차행렬 구했을 때의 결과와 똑같은 것을 확인할 수 있다.
이제 threshold 를 0.4로 해보자.
# Binarizer의 threshold 설정값을 0.4로 설정. 즉 분류 결정 임곗값을 0.5에서 0.4로 낮춤
custom_threshold = 0.4
pred_proba_1 = pred_proba[:,1].reshape(-1,1)
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)
get_clf_eval(y_test , custom_predict)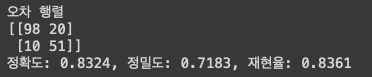
재현율은 높아지고, 반대로 정밀도는 낮아진 것을 확인할 수 있다.
이제 여러개의 Threshold를 변경하면서 예측값을 봐보자.
# 테스트를 수행할 모든 임곗값을 리스트 객체로 저장.
thresholds = [0.4, 0.45, 0.50, 0.55, 0.60]
def get_eval_by_threshold(y_test , pred_proba_c1, thresholds):
# thresholds list객체내의 값을 차례로 iteration하면서 Evaluation 수행.
for custom_threshold in thresholds:
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_c1)
custom_predict = binarizer.transform(pred_proba_c1)
print('임곗값:',custom_threshold)
get_clf_eval(y_test , custom_predict)
get_eval_by_threshold(y_test ,pred_proba[:,1].reshape(-1,1), thresholds )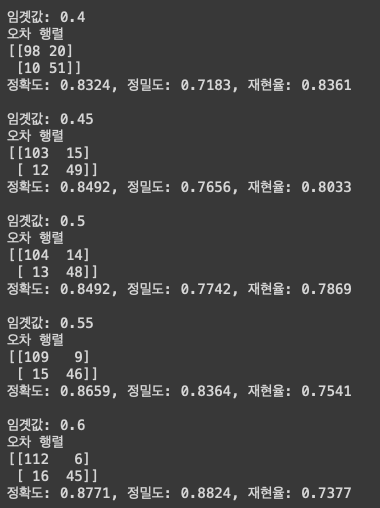
임계값이 점점 올라가면 정밀도도 올라가고, 재현율을 낮아진다.
따라서 뭐가 중요한지는 threshold를 변경해가면서 선택하면 된다.
4. precision_recall_curve()
precision_recall_curve()를 이용하여 threshold에 따른 정밀도-재현율을 봐보자.
from sklearn.metrics import precision_recall_curve
# 레이블 값이 1일때의 예측 확률을 추출
pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1]
# 실제값 데이터 셋과 레이블 값이 1일 때의 예측 확률을 precision_recall_curve 인자로 입력
precisions, recalls, thresholds = precision_recall_curve(y_test, pred_proba_class1 )
print('반환된 분류 결정 임곗값 배열의 Shape:', thresholds.shape)
print('반환된 precisions 배열의 Shape:', precisions.shape)
print('반환된 recalls 배열의 Shape:', recalls.shape)
print()
print("thresholds 5 sample:", thresholds[:5])
print("precisions 5 sample:", precisions[:5])
print("recalls 5 sample:", recalls[:5])
print()
#반환된 임계값 배열 로우가 147건이므로 샘플로 10건만 추출하되, 임곗값을 15 Step으로 추출.
thr_index = np.arange(0, thresholds.shape[0], 15)
print('샘플 추출을 위한 임계값 배열의 index 10개:', thr_index)
print('샘플용 10개의 임곗값: ', np.round(thresholds[thr_index], 2))
print()
# 15 step 단위로 추출된 임계값에 따른 정밀도와 재현율 값
print('샘플 임계값별 정밀도: ', np.round(precisions[thr_index], 3))
print('샘플 임계값별 재현율: ', np.round(recalls[thr_index], 3))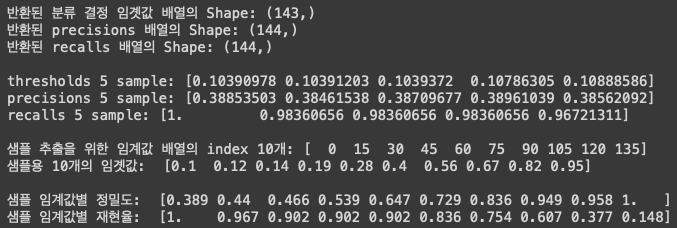
임계값 마다의 정밀도와 재현율을 확인할 수 있다.
그러면 곡선 그림을 그릴 수 있다.
인자는 실제 test값, 예측 확률 값이 들어간다.
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline
def precision_recall_curve_plot(y_test , pred_proba_c1):
# threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출.
precisions, recalls, thresholds = precision_recall_curve( y_test, pred_proba_c1)
# X축을 threshold값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행. 정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
plt.plot(thresholds, recalls[0:threshold_boundary],label='recall')
# threshold 값 X 축의 Scale을 0.1 단위로 변경
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1),2))
# x축, y축 label과 legend, 그리고 grid 설정
plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
plt.legend(); plt.grid()
plt.show()
precision_recall_curve_plot( y_test, lr_clf.predict_proba(X_test)[:, 1] )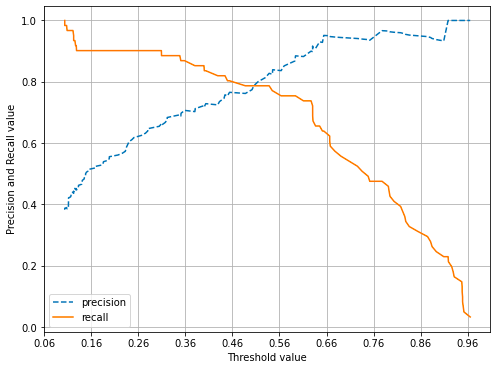
threshold 에 따른 정밀도와 재현율의 변화를 볼 수 있다.
'💡 AI > ML' 카테고리의 다른 글
| ML - Decision Tree (0) | 2021.11.21 |
|---|---|
| ML - F1 score, ROC-AUC (0) | 2021.11.19 |
| ML - 평가(evaluation) (0) | 2021.11.12 |
| ML - fit(), transform() 과 fit_transform()의 차이 (0) | 2021.09.15 |
| ML - Estimator의 fit()과 비지도 학습의 fit()의 차이 (0) | 2021.09.15 |