목차
- Decision Tree 구조
- Decision Tree의 규칙 - 균일도 기반
- Information Gain
- Gini Coefficient (지니 계수)
- Decision Node 생성 프로세스
- Decision Tree의 특징
- Decision Tree 주요 하이퍼 파라미터
- Graphviz를 통한 시각화
- Decision Tree의 Feature 선택 중요도
Classification
- 나이브 베이즈(Naive Bayes) : 베이즈 통게와 생성 모델에 기반한 나이브 베이즈
- 로지스틱 회귀(Logistic Regression) : 독립변수와 종속변수의 선형 관계성에 기반한 로지스틱 회귀
- 결정 트리(Decision Tree) : 데이터 균일도에 따른 규칙 기반의 결정 트리
- 서포트 벡터 머신(Support Vector Machine) : 개별 클래스 간의 최대 분류 마진을 효과적으로 찾아주는 서포트 벡터 머신
- 최소 근접 알고리즘(Nearest Neighbor) : 근접 거리를 기준으로 하는 최소 근접 알고리즘
- 신경망(Neural Network) : 심층 연결 기반의 신경망
- 앙상블(Ensemble) : 서로 다른 머신러닝 알고리즘을 결합한 앙상블
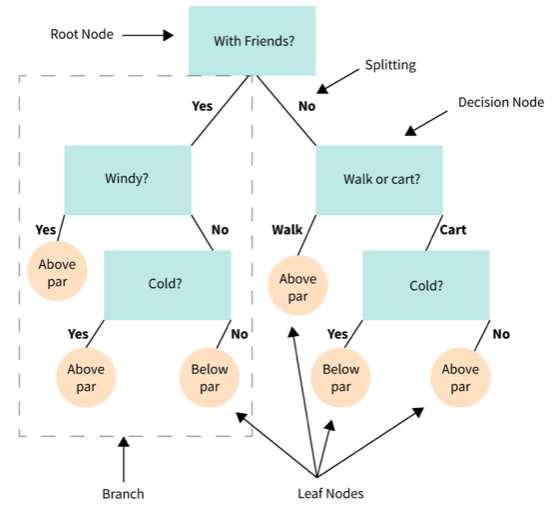
Decision Tree 구조
데이터의 규칙을 학습을 통해 자동으로 찾아내 트리 기반의 분류 규칙을 만든다. (If-Else 기반의 규칙)

- 루트노드(root) : 트리가 시작된 곳(뿌리)
- 규칙노드 : 규칙조건이 되는 곳
- 리프노드 : 결정된 클래스 값, 분류를 마쳤는데 모두 균일하다면 리프노드로 만들어진다.
- 서브트리 : 새로운 규칙 조건마다 생성
Decision Tree의 규칙 - 균일도 기반
결정트리 모델은 어떤 기준으로 규칙을 만들어야 가장 효율적인 분류가 될 것인가가 알고리즘의 성능을 크게 좌우한다.
하지만 규칙이 많다는 것은 좀 더 예측을 위한 학습이 잘된다고 말할 수 있음과 동시에 복잡하다는 의미이며 이는 과적합 으로 이어질 수 있다.
즉, 트리의 깊이(depth)가 깊어질수록 예측 성능이 저하될 가능성이 높기 때문에 적절한 값을 찾아야한다.
가장 적은 노드로 높은 예측을 가지려면 균일하게 나누어야한다(분류시 최대한 많은 데이터가 포함되어야한다).

위의 그림을 보면 A가 가장 균일도가 낮고, C가 가장 균일도가 높다.
이러한 데이터셋의 균일도는 데이터를 구분하는 데 있어서 필요한 정보의 양에 영향을 미친다.
- A의 경우 상대적으로 혼잡도가 높고 균일도가 낮기 때문에 같은 조건에서 데이터를 판단하는데 있어서 더 많은 정보가 필요하다.
- 즉, 더 많은 규칙이 필요하고 그만큼의 새로운 노드들을 거쳐야 한다는 의미이다.
- 또한 노드는 균일도가 높은 데이터 세트를 먼저 선택할 수 있도록 규칙조건을 만든다. 즉, 첫번째 뿌리 노드가 가장 균일도가 높게 쪼갤 수 있는 조건이다.
이러한 정보의 균일도를 측정하는 방법으로는 엔트로피를 이용한 정보이득( Information Gain)지수와 지니계수가 있다.
Decision Tree에서 균일도는 2가지를 기반으로 측정된다.
- Information Gain(엔트로피를 이용한 정보 이득) : 엔트로피는 주어진 데이터 집합의 혼잡도를 의미하는데 서로 다른 값이 섞여 있으면 엔트로피가 높고, 같은 값이 섞여 있으면 엔트로피가 낮다. 정보 이득 지수는 1에서 엔트로피 지수를 뺀 값(1 - 엔트로피지수)이다. 결정 트리는 이 정보 이득 지수가 높은 속성을 기준으로 분할한다.
- Gini Coefficient(지니 계수) : 원래 경제학에서 불평등 지수를 나타낼 때 사용하는 계수로 0이 가장 평등하고 1로 갈수록 불평등하다. 머신러닝에서는 지니 계수가 낮을수록 데이터 균일도가 높은 것으로 해석해 지니 계수가 낮은 속성을 기준으로 분할한다.
Information Gain
- Entrophy 기반 측정 방식
- Information Gain = 1 - Entrophy
- Entrophy = 불확실성 = 데이터의 혼잡도
- 정보가 반복적으로 많이 있으면, 그 정보가 가지는 기대값은 낮다.
- 정보가 자주 나타나지 않고, 빈번하지 않고, 예측 불가능 하다면, 그 정보의 효용성은 높다.
- 다른 값이 섞여 있다 = Entrophy가 높다
- 같은 값이 섞여 있다 = Entrophy가 낮다
- Decision Tree는 IG 값이 높은 속성을 기반으로 분할한다.
Gini Coefficient (지니 계수)
- 경제학에서 나온 불평등 지수
- 0에서 가장 평등 → 1로 갈수록 불평등
- Gini Coefficient 낮을 수록 균일도가 높다
- Decision Tree는 Gini Coefficient 값이 낮아지는 방향으로 분할한다.
Decision Node 생성 프로세스
- 데이터 집합의 모든 아이템이 같은 분류에 속하는지 확인한다.
- If true : leaf node로 만들어서 분류 결정
- else : 데이터를 분할하는데 가장 좋은 속성과 분할 기준을 찾는다. (IG 또는 GC 이용)
- 해당 속성과 분할 기분으로 Branch 생성
- 1~3 반복
Decision Tree의 특징
장점
- 정보의 균일도라는 룰을 기반으로 하고 있어서 알고리즘이 쉽고 직관적이다.
- 정보의 균일도만 신경쓰면 되므로 특별한 경우를 제외하고는 각 피처의 스케일링과 정규화 같은 전처리 작업이 필요없다.
- 선형회귀 모델과 달리 특성들간의 상관관계가 많아도 트리모델은 영향을 받지 않는다.
- 비선형 모델에서 또한 depth를 조절(하이퍼파라미터를 수정하여)함으로서 모델을 학습할 수 있다.
- 수치형, 범주형 데이터 모두가능하다.
- 회귀와 분류 모두 가능하다.
단점
- 새로운 sample이 들어오면 속수무책이다.
- 학습정확도를 높이기 위해서는 더 복잡하게 만들어야 하는데 그러다 보면 과적합(Overfitting)에 걸리기 매우 쉽다.
Decision Tree 주요 하이퍼 파라미터
- max_depth : 트리의 최대 길이
- 디폴트는 None = 균일한 값이 나올 때까지 계속 분할
- min_samples_split보다 작아질 때까지 분할
- max_features : 최적의 분할을 위해 고려할 최대 피쳐 개수
- 디폴트는 None
- min_samples_split : node를 분할하기 위한 최소한의 샘플 데이터 수
- Overfitting(과적합) 제어하기 위해 사용된다.
- 디폴트는 2
- 작게 설정할수록 분할되는 노드가 많아져서 Overfitting 가능성 증가
- min_samples_leaf : leaf node가 되기 위한 최소한의 샘플 데이터 수
- Overfitting(과적합) 제어하기 위해 사용된다.
- 특정 클래스의 데이터가 극도로 작을 수 있으므로, min_samples_leaf는 작게 설정해야 한다.
- max_leaf_nodes : leaf node의 최대 갯수
Graphviz를 통한 시각화

아래 코드를 실행하면 위와 같이 시각화 된다.
petal length <= 2.45 : 자식 노드를 만들기 위한 규칙 조건이다. 이 조건이 없으면 리프노드이다.
gini : value=[] 로 주어진 데이터 분포에서의 Gini Coefficient 이다.
samples : 한 규칙에 해당하는 데이터 수
value=[] : 클래스 값 기반의 데이터 수
색깔이 진할수록 단일한 분류값으로 균일화 되어 있다.
연하면 불확실성이 높음
위의 트리는 max_depth가 정해지지 않았기 때문에 끝까지 분할한다.
min_samples_leaf(샘플이 n개 이상이면 그만 쪼개자) 나 min_samples_split(샘플이 n개 이상이면 쪼개야 한다) 을 설정하여 분할할 수도 있다.
코드
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
# DecisionTree Classifier 생성
dt_clf = DecisionTreeClassifier(random_state=156)
# 붓꽃 데이터를 로딩하고, 학습과 테스트 데이터 셋으로 분리
iris_data = load_iris()
X_train , X_test , y_train , y_test = train_test_split(iris_data.data, iris_data.target,
test_size=0.2, random_state=11)
# DecisionTreeClassifer 학습.
dt_clf.fit(X_train , y_train)
from sklearn.tree import export_graphviz
# export_graphviz()의 호출 결과로 out_file로 지정된 tree.dot 파일을 생성함.
export_graphviz(dt_clf, out_file="tree.dot", class_names=iris_data.target_names , \
feature_names = iris_data.feature_names, impurity=True, filled=True)
import graphviz
# 위에서 생성된 tree.dot 파일을 Graphviz 읽어서 Jupyter Notebook상에서 시각화
with open("tree.dot") as f:
dot_graph = f.read()
graphviz.Source(dot_graph)Decision Tree의 Feature 선택 중요도
사이킷런의 DecisionClassifier 객체에는 feature_importances_ 를 통해 중요한 Feature들을 선택할 수 있게 정보를 제공한다.
얼마나 자주 쪼개지는데에 활용이 되느냐 를 의미
import seaborn as sns
import numpy as np
%matplotlib inline
# feature importance 추출
print("Feature importances:\n{0}".format(np.round(dt_clf.feature_importances_, 3)))
# feature별 importance 매핑
for name, value in zip(iris_data.feature_names , dt_clf.feature_importances_):
print('{0} : {1:.3f}'.format(name, value))
# feature importance를 column 별로 시각화 하기
sns.barplot(x=dt_clf.feature_importances_ , y=iris_data.feature_names)
4개의 속성이 나왔다.
'💡 AI > ML' 카테고리의 다른 글
| ML - interview (0) | 2022.04.11 |
|---|---|
| ML - Ensemble Learning (0) | 2021.11.22 |
| ML - F1 score, ROC-AUC (0) | 2021.11.19 |
| ML - Confusion Matrix, Precision, Recall (0) | 2021.11.18 |
| ML - 평가(evaluation) (0) | 2021.11.12 |