선형대수 용어 정리
- 고유벡터(eigen vector) : 선형변환했을 때 방향은 변하지 않고 크기만 변하는 벡터
- 고유값(eigen value) : 고유벡터가 변환되는 크기
- 행렬식(deteminant) : ad-bc, 부피
- determinant = 0 : 행렬을 구성하는 벡터가 서로 동일선상(colinear)에 있다는 것
- 기저(basis) : 벡터 공간을 생성하는 선형독립인 벡터들
- 벡터공간(Vector space) : basis로 생성 가능한 공간
- 부분공간(Subspace) : 전체 공간의 일부분
- Span : 기저 벡터들로 구성되는 2차원 부분 공간
- 랭크(Rank) : 행렬의 열벡터에 의해 span된 벡터공간의 차원
- 정규 직교 기저 : 벡터의 크기가 1이고 서로 수직인 기저 벡터, A-1 = AT, AAT = ATA = I
- 직교 행렬(Orthogonal Matrix) : 행벡터와 열벡터가 유클리드 공간의 정규 직교 기저를 이루는 실수 행렬
- 행렬에서의 닮음(Similar) : P^(-1) A P = B 를 만족하는 P가 존재할 때, 정사각행렬 A와 B는 닮음이다.
- 직교 닮음(Orthogonal similar) : P^(T) A P = B 일때 B는 A에 직교 닮음
- 직교 대각화(Orthohonal diagonalizable) : P^(T) A P = B 일때, P는 A를 직교 대각화 한다. A는 직교 대각화 가능. 이때 A는 반드시 대칭행렬
- 고유값 분해(eigenvalue decomposition) : A를 (고유벡터) x (고유값[대칭행렬]) x (고유벡터T) 로 분해함
- 특이값 분해(Singular Value Decomposition) :
- 차원을 축소한 행렬을 찾는 데 사용됨.
- n x p 행렬에서 n개의 점을 표현할 수 있는 p차원 공간을 찾는 문제
- n x p 행렬 A에 대하여, A^T x A의 고유값을 람다1, 2, ..라 했을 때, 특이값(singular value)은 람다의 루트를 취한 값이다.



행렬은 선형변환이고 함수이다 라고 했는데.. 이쯤 정말 궁금한 것!
- 행렬(선형 변환)이 '함수' 라면 함수의 근본적인 정의를 정말 만족할 수 있을까?
- 입력과 출력이 있다고 다 함수일까?
- 즉, '선형 변환'은 엄밀하게 함수라고 부를 수 있는 걸까?
함수의 정의를 다시 보자.

정의역, 공역, 치역은 어떻게 선형대수에서 나타나나?

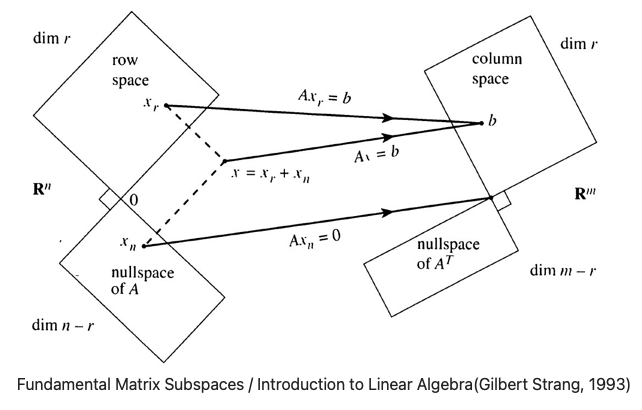
정의역은 Row space + Null space
모든 공간에 있는 벡터들을 다 모두 이용해야지만 임의의 입력벡터 하나를 표현할 수 있다.
잠깐! 부분 공간이란?


원점을 지나지 않은 직선은 부분 공간이 될 수 없다.
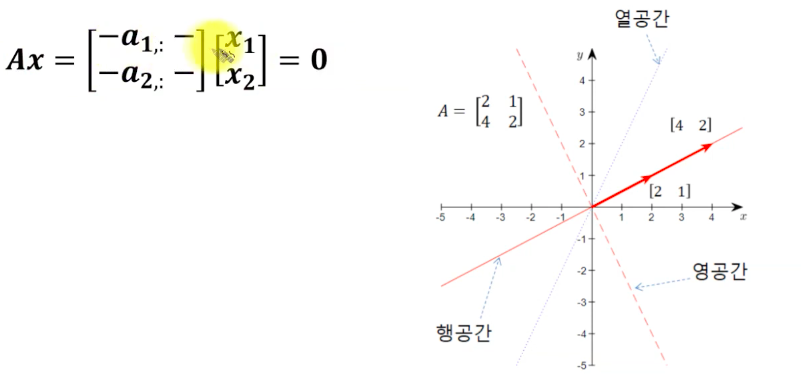
행공간과 열공간

행공간(Row space) : 행벡터들만 가지고 구성된 공간
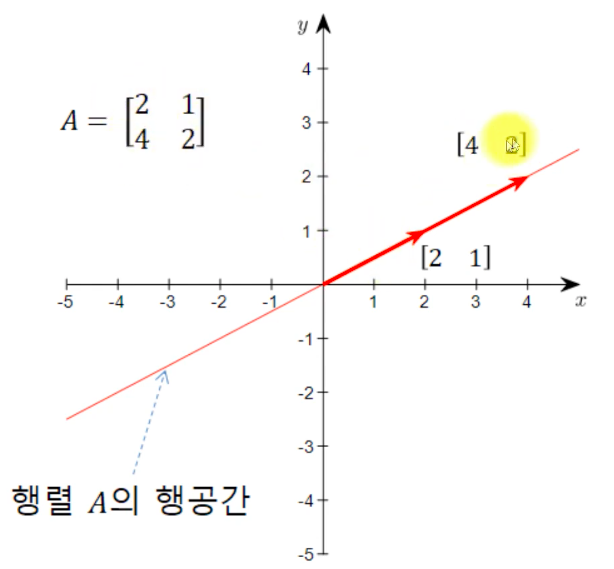
열공간(Column space) : 열벡터들만 가지고 구성된 공간

영공간 : 모두 0을 출력하게 만들어주는 입력 벡터

선형 변환 후에 0이 되는 입력들이 어디있을까? 를 말한다.
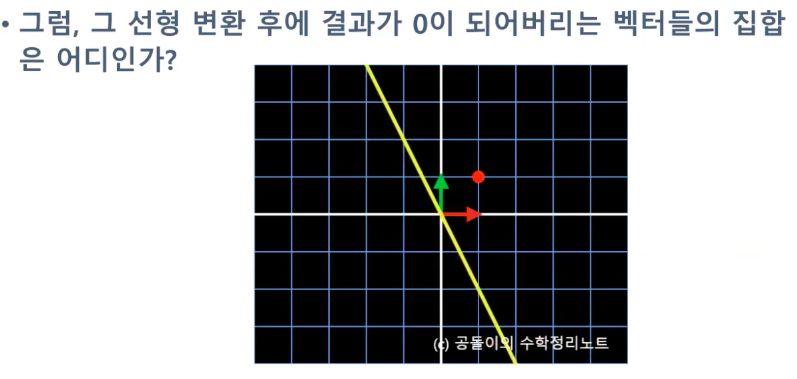
노란색 선상에 있던 벡터들은 선형 변환 후에 모두 0이 된다.
즉, 영공간이 얘기하고 싶은 것은 선형 변환 후에 모두 0이 되는 입력 벡터들의 집합이다 라는 것이다.
행공간과 영공간은 직교한다.
정리

n by n 행렬에서
n차원은 row space와 null space로 구성되어 있고,
null space에 있는 벡터는 선형변환하면 모두 0이 된다.
row space에 있는 벡터는 모두 column space로 이동하게 되는데,
row space에 있는 벡터와 null space에 있는 벡터들을 합쳐도 똑같이 모두 column space로 이동하게 된다.
왜냐하면 null space에 있는 벡터는 선형변환하면 모두 0이 되기 때문이다.
'✏️ Mathemathics > Linear Algebra' 카테고리의 다른 글
| 선형대수 - Eigen vector(고유 벡터), Eigen value(고유 값)의 기하학적 의미 (0) | 2021.08.17 |
|---|---|
| 선형대수 - 행렬식과 역행렬의 기하학적 의미 (0) | 2021.07.20 |
| 선형대수 - 행렬과 선형변환 (0) | 2021.07.19 |
| 선형대수 - 행벡터의 의미와 벡터의 내적 (0) | 2021.07.16 |
| 선형대수 - 행렬 곱에 대한 또 다른 시각 (0) | 2021.06.23 |