선형대수 - Eigen vector(고유 벡터), Eigen value(고유 값)의 기하학적 의미

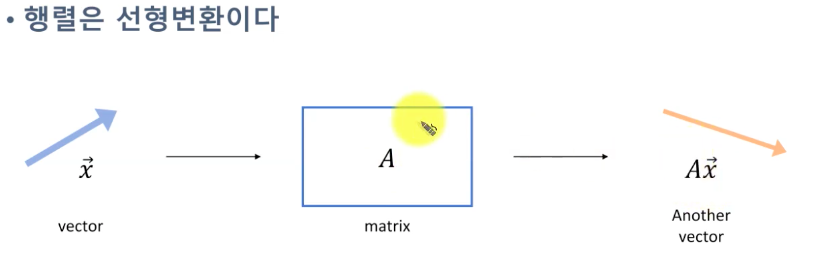
행렬에 벡터를 넣어주면 다른 벡터가 나온다.

행렬은 선형변환이다 = 행렬은 일종의 함수처럼 작동한다.

---

선형 변환이 되어서 (3,3)의 결과가 나온다.

 

어떤 벡터들은 선형 변환 시 크기만 바뀌고 방향이 바뀌지 않을 수 있다.

---

Eigen value, Eigen vector

고유 벡터 : 벡터 x에 행렬을 곱해줬을 때(선형변환 시켜줬을 때), 크기만 변하고 원래 벡터와 평행한 벡터

 

Eigen vector(고유 벡터) : 입력 벡터 x를 A로 선형변환 시킨 결과 Ax가 그저 x가 상수배 된 벡터

여기서 x 가 Eigen vector(고유 벡터), 변한 크기인 람다가 Eigen Value(고유값)이 된다.

---

 

---

(A-람다 I) 가 역행렬을 가지게 되면,

(A-람다 I)x = 0 에 역행렬을 곱해주면 x = 0 이 되므로 모순이 된다.

 

 

 

따라서 (A-람다I) 가 0이 된다면

(A-람다I) 는 역행렬을 갖지 않게 된다.

 

 

계수를 적절하게 곱해서 연립방정식을 풀어주면

 

λ = 1인 경우에 고유 벡터는 (1,-1)

λ = 3인 경우에 고유 벡터는 (1,1) 이다.

 

---

고유벡터의 기하학적 의미를 살펴보자

λ = 1인 경우에 고유 벡터는 (1,-1)

λ = 3인 경우에 (1,1)

 

(1,1) 선상의 벡터는 방향은 안바뀌고, 크기만 바뀌고

(1,-1) 선상의 벡터는 방향도 바뀌지 않고, 크기도 바뀌지 않는다.

 

 

Ref : https://angeloyeo.github.io/2019/07/17/eigen_vector.html