선형대수 - 행렬과 선형변환

---

행렬의 곱이라는 것은 두 열벡터의 선형 결합으로 볼 수 있지 않을까? 의 관점으로 볼 수 있다.

 

 

 

 

행렬 자체가 열벡터에 대한 함수로 작동할 수 있다.

 

---

함수인데 특정한 규칙이 정해진 함수라고 생각할 수 있다.

 

 

임의의 벡터 →a, →b와 스칼라 c 에 대하여 변환 T 가 다음의 두 조건을 만족한다면 이 변환 T 는 선형변환이다.

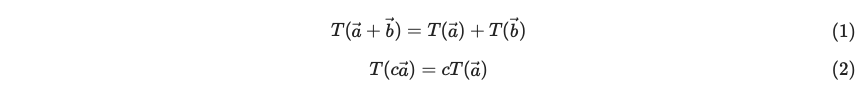
따라서, 위의 선형 변환의 성질에 따라, 임의의 벡터 (x, y)에 대해서

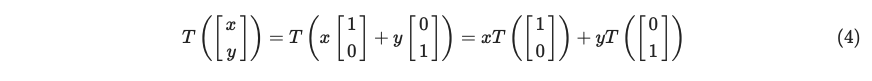
다음이 성립한다.

x와 y는 분리가 된다.

 

원래의 기저 벡터 두 개를 아래와 같이 ^i, ^j 라 하고,

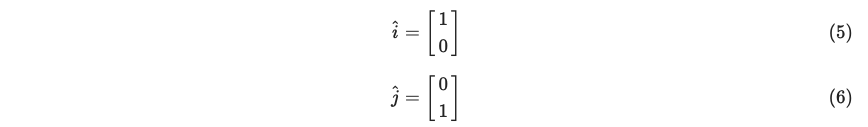
새로운 기저 벡터를 ^inew, ^jnew 라 했을 때,

T 가 선형변환이라면, 벡터 [x y] 는 선형 변환 후에

새로운 기저 벡터 ^inew 와 ^jnew 의 x 배와 y 배의 합으로 표현되어야 한다는 것이다.

---

 

새로운 빨간 점은 새로운 기저벡터 들의 합으로 표현된다.

이것이 선형 변환이 가져다 주는 의미이다.

 

 

---

여러 선형 변환의 시각적 예시

 

 

Ref : https://angeloyeo.github.io/2019/07/15/Matrix_as_Linear_Transformation.html