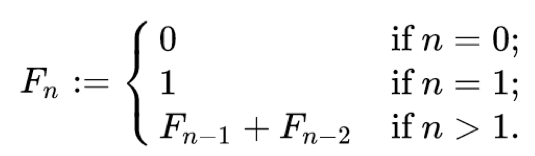
Published 2021. 7. 23. 15:30
1. 1. 정의
1.1. 동적계획법 (DP 라고 많이 부름)
- 입력 크기가 작은 부분 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서, 보다 큰 크기의 부분 문제를 해결, 최종적으로 전체 문제를 해결하는 알고리즘
- 상향식 접근법으로, 가장 최하위 해답을 구한 후, 이를 저장하고, 해당 결과값을 이용해서 상위 문제를 풀어가는 방식
- Memoization 기법을 사용함 : 작은 문제들을 기억하는 것
- Memoization (메모이제이션) 이란: 프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하지 않도록 하여 전체 실행 속도를 빠르게 하는 기술 -> 동일한 문제를 풀지 않도록 하는 것
- Memoization (메모이제이션) 이란: 프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하지 않도록 하여 전체 실행 속도를 빠르게 하는 기술 -> 동일한 문제를 풀지 않도록 하는 것
- 문제를 잘게 쪼갤 때, 부분 문제는 중복되어, 재활용됨
- 예: 피보나치 수열
1.2. 분할 정복
- 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘
- 하향식 접근법으로, 상위의 해답을 구하기 위해, 아래로 내려가면서 하위의 해답을 구하는 방식
- 일반적으로 재귀함수로 구현
- 일반적으로 재귀함수로 구현
- 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않음
- 예: 병합 정렬, 퀵 정렬 등
2. 2. 공통점과 차이점
2.1. 공통점
- 문제를 잘게 쪼개서, 가장 작은 단위로 분할
2.2. 차이점
동적 계획법
- 부분 문제는 중복되어, 상위 문제 해결 시 재활용됨
- Memoization 기법 사용 (부분 문제의 해답을 저장해서 재활용하는 최적화 기법으로 사용)
분할 정복
- 부분 문제는 서로 중복되지 않음
- Memoization 기법 사용 안함
3. 3. 동적 계획법 알고리즘 이해

함수를 fibonacci 라고 하면,
fibonacci(0):0
fibonacci(1):1
fibonacci(2):1
fibonacci(3):2
fibonacci(4):3
fibonacci(5):5
fibonacci(6):8
fibonacci(7):13
fibonacci(8):21
fibonacci(9):34

f(1), f(2), f(3) 등의 문제가 겹치므로
이 결과 값들을 따로 저장해 놓는다 : memoization
3.1.1. 재귀
def fibo(n):
if n <= 1:
return n
return fibo(n-1) + fibo(n-2)
3.1.2. 동적 계획법 활용
def fibo_dp(n)
cache = [0 for i in range(n+1)] # 0으로 저장된 일종의 리스트가 만들어진다.
cache[0] = 1
cache[1] = 1
for i in range(2, n+1):
cache[i] = cache[i-1] + cache[i-2]
return cache[n]
캐시를 n+1개 만드는 이유

n+1 개 만들어야 마지막 n에 대한 값을 저장할 수 있다.

다음 값을 계산할 때는 해당 값의 전 2개의 배열 안에 있는 값으로 계산한다.
해당 인덱스의 값을 가져와서 저장된 값으로 계산해버린다.
그냥 재귀를 쓰는 방법과 다르다.
그냥 재귀를 쓰면 계속 값을 계산하게 된다.
동적 계획법은 값을 저장함으로써 memoization 기법을 사용한다.
'🕶 Algorithm > 알고리즘' 카테고리의 다른 글
| 병합 정렬 (Merge sort) (0) | 2021.08.06 |
|---|---|
| 퀵정렬 (Quick sort) (0) | 2021.07.23 |
| 재귀 (Recursion) (0) | 2021.07.22 |
| 삽입 정렬 (Insertion sort) (0) | 2021.07.21 |
| 선택 정렬 (Select sort) (0) | 2021.07.21 |