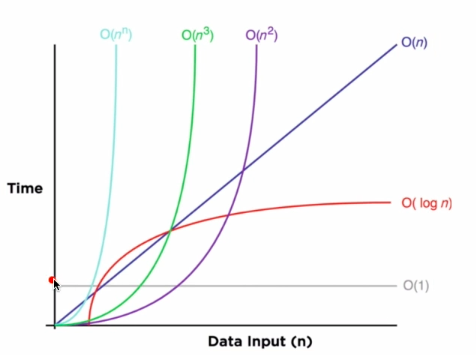
알고리즘 복잡도 계산이 필요한 이유
시간복잡도 : 알고리즘의 풀이 시간을 정략적으로 표기하는 방법
하나의 문제를 푸는 알고리즘은 다양할 수 있음. 즉, 풀이가 다양하다.
정수의 절대값 구하기
- 1, -1 ->> 1
- 방법1: 정수값을 제곱한 값에 다시 루트를 씌우기
- 방법2: 정수가 음수인지 확인해서, 음수일 때만, -1을 곱하기
다양한 알고리즘 중 어느 알고리즘이 더 좋은지를 분석하기 위해, 복잡도를 정의하고 계산함
알고리즘 복잡도 계산 항목
- 시간 복잡도: 알고리즘 실행 속도
- 공간 복잡도: 알고리즘이 사용하는 메모리 사이즈
가장 중요한 시간 복잡도를 꼭 이해하고 계산할 수 있어야 함
알고리즘 시간 복잡도의 주요 요소
반복문을 가지고 시간복잡도를 계산한다.
시간이 어디에서 제일 많이 걸리느냐를 보면 반복문이다.
생각해보기: 자동차로 서울에서 부산을 가기 위해, 다음과 같이 항목을 나누었을 때, 가장 총 시간에 영향을 많이 미칠 것 같은 요소는?
ex) 자동차로 서울에서 부산가기
- 자동차 문열기
- 자동차 문닫기
- 자동차 운전석 등받이 조정하기
- 자동차 시동걸기
- 자동차로 서울에서 부산가기
- 자동차 시동끄기
- 자동차 문열기
- 자동차 문닫기
입력의 크기가 커지면 커질수록 반복문이 알고리즘 수행 시간을 지배함
알고리즘 성능 표기법
Big O (빅-오) 표기법: O(N)
- 알고리즘 최악의 실행 시간을 표기
- 가장 많이/일반적으로 사용함
- 아무리 최악의 상황이라도, 이정도의 성능은 보장한다는 의미이기 때문
Ω (오메가) 표기법: Ω(N)
- 오메가 표기법은 알고리즘 최상의 실행 시간을 표기
Θ (세타) 표기법: Θ(N)
- 오메가 표기법은 알고리즘 평균 실행 시간을 표기
시간 복잡도 계산은 반복문이 핵심 요소임을 인지하고, 계산 표기는 최상, 평균, 최악 중, 최악의 시간인 Big-O 표기법을 중심으로 익히면 됨
빅 오 표기법 (Big-O 표기법)
O(입력)
- 입력 n 에 따라 결정되는 시간 복잡도 함수
- O(1), O(𝑙𝑜𝑔𝑛), O(n), O(n𝑙𝑜𝑔𝑛), O(𝑛^2), O(2^𝑛), O(n!)등으로 표기함
- 입력 n 의 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있음
- O(1) < O(𝑙𝑜𝑔𝑛) < O(n) < O(n𝑙𝑜𝑔𝑛) < O(𝑛^2) < O(2^𝑛) < O(n!)
- 참고: log n 의 밑은 2이다.
- O(1) < O(𝑙𝑜𝑔𝑛) < O(n) < O(n𝑙𝑜𝑔𝑛) < O(𝑛^2) < O(2^𝑛) < O(n!)
- 단순하게 입력 n에 따라, 몇번 실행이 되는지를 계산하면 된다.
- 표현식에 가장 큰 영향을 미치는 n 의 단위로 표기합니다.
O(1)
n이 1이든 100이든, 1000이든, 10000이든 실행을 무조건 2회(상수회) 실행한다.
if n > 10:
print(n)O(n)
n에 따라, n번, n + 10 번,
또는 3n + 1 번등 실행한다.
variable = 1
for num in range(3):
for index in range(n):
print(index)O(𝑛^2)
n에 따라, 𝑛^2번, 𝑛^2 + 1000 번, 100𝑛^2 - 100,
또는 300𝑛^2 + 1 번등 실행한다.
variable = 1
for i in range(300):
for num in range(n):
for index in range(n):
print(index)

만약 시간 복잡도 함수가 2𝑛^2 + 3n 이라면
- 가장 높은 차수는 2𝑛^2
- 상수는 실제 큰 영향이 없음
- 결국 빅 오 표기법으로는 O(𝑛^2)
1부터 n까지의 합을 구하는 알고리즘1
def _sum_(n):
total = 0
for i in range(1,n+1):
total += i
return = total시간복잡도 : O(n)
1부터 n까지의 합을 구하는 알고리즘2
(n x (n+1)) / 2
def sum_all(n):
return int(n * (n + 1) / 2)시간복잡도 : O(1)
성능 : 알고리즘2 > 알고리즘1
'🕶 Algorithm > 자료구조' 카테고리의 다른 글
| 공간복잡도 (0) | 2021.07.22 |
|---|---|
| 트리 (0) | 2021.07.20 |
| 해쉬 테이블 (0) | 2021.07.19 |
| 연결 리스트 (Linked List) (0) | 2021.07.16 |
| 자료구조, 알고리즘, 배열, 스택, 큐 (0) | 2021.07.15 |