문제
이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.

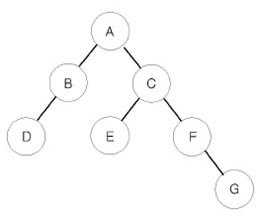
예를 들어 위와 같은 이진 트리가 입력되면,
- 전위 순회한 결과 : ABDCEFG // (루트) (왼쪽 자식) (오른쪽 자식)
- 중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
- 후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)
가 된다.
입력
첫째 줄에는 이진 트리의 노드의 개수 N(1≤N≤26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 영문자 대문자로 매겨지며, 항상 A가 루트 노드가 된다. 자식 노드가 없는 경우에는 .으로 표현된다.
출력
첫째 줄에 전위 순회, 둘째 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파벳을 공백 없이 출력하면 된다.

코드
class Node:
def __init__(self, item, left, right):
self.item = item
self.left = left
self.right = right
# 전위 순회
def preorder(node):
print(node.item, end='')
if node.left != '.':
preorder(tree[node.left])
if node.right != '.':
preorder(tree[node.right])
# 중위 순회
def inorder(node):
if node.left != '.':
inorder(tree[node.left])
print(node.item, end='')
if node.right != '.':
inorder(tree[node.right])
# 후위 순회
def postorder(node):
if node.left != '.':
postorder(tree[node.left])
if node.right != '.':
postorder(tree[node.right])
print(node.item, end='')
N = int(input())
tree = {}
for _ in range(N):
node, left, right = map(str, input().split())
tree[node] = Node(item=node, left=left, right=right)
preorder(tree['A'])
print()
inorder(tree['A'])
print()
postorder(tree['A'])
트리 문제이다.
부모 노드와 자식 노드를 만들기 위해 class를 사용하였다.
전위 순회는 루트 노드를 먼저 방문한다.
중위 순회는 왼쪽 하위 트리를 방문한 후 루트 노드를 방문한다.
후위 순회는 하위 트리를 모두 방문한 후 루트 노드를 방문한다.
따라서 전위 순회는 해당 노드를 먼저 출력해주고 왼쪽 자식노드, 오른쪽 자식노드 순으로 방문해주면 된다.
중위 순회는 왼쪽 자식노드를 먼저 방문하고, 해당 노드를 출력한 후, 오른쪽 자식노드를 방문하면 된다.
후위 순회는 왼쪽 자식노드, 오른쪽 자식노드 순으로 먼저 방문한 후 해당 노드를 출력하면 된다.
트리는 딕셔너리 형태로 만들어주었다.
입력받은 노드의 갯수만큼 반복해주며
입력받은 노드를 key 값으로 하고 value 는 객체로 받는다.
딕셔너리도 알고 있었고 객체를 만드는 것도 알고 있었지만 딕셔너리의 value를 객체로 받을 수 있다는 것을 처음 알게 되었다.
C의 연결리스트로만 트리를 구현해보았는데 파이썬은 딕셔너리와 객체를 연결함으로써 구현할 수 있다.
Reference: jjangsungwon.tistory.com/12
'⏰ 코딩테스트 > 백준 알고리즘' 카테고리의 다른 글
| 백준 알고리즘 - 1932 - 정수삼각형 (0) | 2021.02.01 |
|---|---|
| 백준 알고리즘 - 11725 - 트리의 부모 찾기 (0) | 2021.01.31 |
| 백준 알고리즘 - 9095 - 1, 2, 3 더하기 (0) | 2021.01.25 |
| 백준 알고리즘 - 2447 - 별찍기 (0) | 2021.01.12 |
| 백준 알고리즘 - 2630 - 색종이 만들기 (0) | 2021.01.11 |