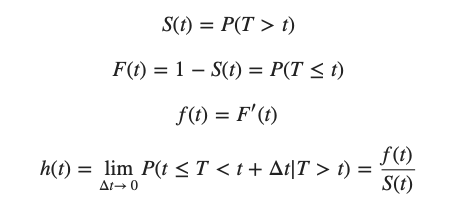
모수적 방법(parametric method): 관측 값이 어느 특정한 확률분포, 예를 들면 정규분포, 이항분 포 등을 따른다고 전제한 후 그 분포의 모수(parameter)에 대한 검정을 실시하는 방법이다.
비모수적 방법(nonparametric method): 관측 값이 어느 특정한 확률분포를 따른다고 전제할 수 없거나 또는 모집단에 대한 아무런 정보가 없는 경우에 실시하는 검정방법으로 모수에 대한 언급 이 없으며 분포무관 방법이라고도 한다. 요약하면 자료가 정규분포가 아니거나 표본의 크기가 작으면 분포에 대한 기본가정을 필요로 하지 않는 통계적 기법이다.

- Non-parametric: 데이터의 feature와 생존 시간 분포 정보를 사용하지 않는 방법입니다. 분포 정보를 알 수 없을 때 유용하지만 예측이 부정확할 수 있습니다.
- Semi-parametric: feature 정보를 활용하지만, 생존 시간 분포 정보를 사용하지 않는 방법입니다. Cox Proportional Hazard 모델이 해당합니다.
- Parametric: 생존 시간 분포가 존재한다고 가정하고 회귀 모델로 생존 시간을 예측하는 기법입니다. 지수 분포, 베이불(Weibull) 분포, 로지스틱(Logistic) 분포, 정규 분포 등을 사용합니다.
생존분석함수
생존분석 함수는 개인의 생존시간 T가 확률변수 (random variable) 라고 생각했을 때 이와 관련된 함수를 의미한다.
Survival function
S(t) = P(T > t)
: 특정 시점 t에서 살아 있을 확률을 나타내는 함수이다. 즉, 이것은 event time T가 t보다 클 확률이다.
F(t) : 특정시점 t까지 event가 발생했을 확률을 말한다. 이는 1-S(t)이다. f(t)의 cdf (cumulative density function)이다.
f(t) : 특정 시점 t에서 event가 발생할 확률을 나타내는 함수이다. (이것은 probability density function 이다.) 그리고 f(t)는 F(t)의 t에 대한 미분이다.
Hazard function
h(t) : t까지 살았을 때, 직후에 바로 event가 일어날 조건부 확률을 나타낸다.
h(t) = f(t)/S(t) 로 나타내어 지는데, 아래 식을 통해 확인해 보자.
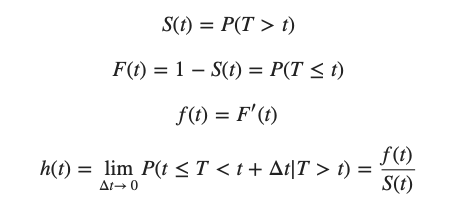
직접 f(t)/S(t)를 계산해보면 조건부확률의 계산공식을 통해 양변이 같다는 것을 확인할 수 있다.

why? h(t) 라는 것은 1-S(t)를 미분한 것을 다시 S(t) 로 나눈 것이다. 이를 만족하는 S(t)는 위의 S(t) 밖에 없다. (if and only if 이다.)
Kaplan-Meier estimation
관찰 시간에 따라 사건이 발생한 시점의 사건 발생률을 계산하는 생존 분석 방법
Censoring이 있는 데이터에서 생존함수를 추정하는 비모수적인 방법이다. 만약 censoring이 아예 없다면, 생존함수는 그 시점에서 살아있는 사람을 보면 된다. 하지만 right-censoring이 있는 경우 해당시점에서 살아있는 사람은 censoring 된 사람을 제외한 사람일 것이고, 이 경우에 살아있는 사람만 계산하게 되면 생존 함수가 잘못 추정되게 된다. 따라서 censoring이 있을 때, 그 사람이 t시점까지 살았다는것을 활용하여 각 시점에서 survival rate을 구하여 계속 곱하면서 survival function을 추정한다.

점선은 20년에서 전체 환자 그룹의 36퍼센트가 생존해있다는 것을 말한다.
콕스 비례위험모형 (Cox's proportional hazard model)
hyperconnect.github.io/2019/08/22/survival-analysis-part2.html
Survival Analysis (2/3)
Survival Analysis를 활용한 고객 이탈 예측 방법을 소개합니다.
hyperconnect.github.io
reference
모수적, 비모수적 방법 : contents.kocw.net/KOCW/document/2013/koreasejong/HongSungsik4/13.pdf
콕스 : bioinformaticsandme.tistory.com/223
생존분석함수 : https://3months.tistory.com/349 [Deep Play]
'📌 Paper > Deepsurv' 카테고리의 다른 글
| Deepsurv - 실행 과정 (0) | 2021.01.20 |
|---|---|
| Deepsurv - method 및 관련 개념 (0) | 2021.01.18 |
| Deepsurv 논문 읽기 (0) | 2021.01.11 |
| Tensorflow - Theano - Torch - Keras - Lasagne (0) | 2021.01.04 |
| Deepsurv 설치 및 실행 과정 (0) | 2021.01.04 |