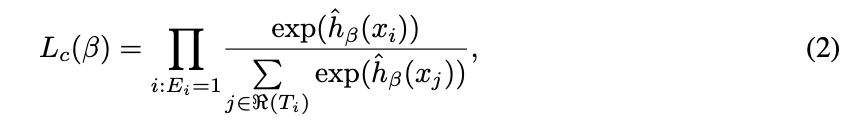
3 Methods
In this section, we describe our methodology for providing personalized treatment recommendations using DeepSurv. First, we describe the architecture and training details of DeepSurv, an open source Python module that applies recent deep learning techniques to a nonlinear Cox proportional hazards network. Second, we define DeepSurv as a prognostic model and show how to use the network’s predicted risk function to provide personalized treatment recommendations.
Deepsurv를 이용하여 개인 맞춤 치료법 제공하는 방법을 소개한다.
첫번째로 Deepsurv의 구조와 훈련 상세를, 비선형 콕스 비례 위험 네트워크로 학습한 파이썬 모듈을 사용한다.
두번째로 Deepsurv를 prognostic 모델로 define하고, 개인 맞춤 치료법 추천을 어떻게 predicted risk 함수를 이용해서 할지 말할 것이다.
3.1 DeepSurv
DeepSurv is a multi-layer. perceptron, which predicts a patient’s risk of death. The output of the network is a single node, which estimates the risk function hθ(x) parameterized by the weights of the network θ. Similar to the Faraggi-Simon network, we set the loss function to be the negative log partial likelihood of Equation 2:
Deepsurv는 환자의 사망 위험을 예측하는 다중 레이어 인공신경망 모델이다.
손실 함수(Loss function = Cost function)를 (2) 방정식을 통해 설정한다.
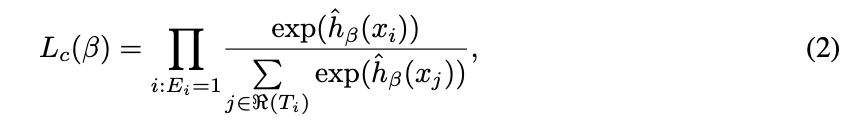

We allow a deep architecture (i.e. more than one hidden layer) and apply modern techniques such as weight decay regularization, Rectified Linear Units (ReLU) [17] with batch normalization [18], Scaled Exponential Linear Units (SELU) [19], dropout [20], gradient descent optimization algo- rithms (Stochastic Gradient Descent and Adaptive Moment Estimation (Adam) [21]), Nesterov mo- mentum [22], gradient clipping [23], and learning rate scheduling [24].
To tune the network’s hyper-parameters, we perform a Random hyper-parameter optimization search [25]. For more technical details, see Appendix A.
3.2 Treatment recommender system
In a clinical study, patients are subject to different levels of risk based on their relevant prognostic features and which treatment they undergo. We generalize this assumption as follows. Let all patients in a given study be assigned to one of n treatment groups τ ∈ {0, 1, ..., n − 1}. We assume each treatment i to have an independent risk function hi(x). Collectively, the hazard function becomes:
이러한 가정을 일반화 하였다.
연구에 참여하는 모든 환자들 n개중 하나의 treatment 그룹에 할당되게 하였다.
그리고 각각의 treatment를 독립된 risk funtion인 hi(x)에 적용하였다.
harzard function은 다음과 같다.

perceptron : 인공신경망모델
risk function :
loss : 모델의 예측과 정답 사이에 얼마나 차이가 있는지 나타내는 측도(measure). 이 값을 정하기 위해서는 손실함수(loss function)이 정의되어 있어야 한다. 예컨대 선형회귀 모델에서 손실함수는 대개 Mean Squared Error, 로지스틱회귀에서는 로그우도가 쓰인다.
likelihood(우도) : 우도 (尤度, likelihood) 란, 어떤 시행의 결과 (Evidence) E 가 주어졌다 할 때, 만일 주어진 가설 H 가 참이라면, 그러한 결과 E 가 나올 정도는 얼마나 되겠느냐 하는 것이다. 즉 결과 E 가 나온 경우, 그러한 결과가 나올 수 있는 여러 가능한 가설들을 평가할 수 있는 측도가 곧 우도인 셈이다.
Maximum Likelihood Estimation : 딥러닝 모델을 학습시키기 위해 최대우도추정 기법을 쓴다.
여러 가설 중 그 우도가 최대가 되는 가설을 선호함은 자연스러운 일이다. 즉 만일 그 가설이 어떤 모집단의 모수 (population parameter) 에 관한 가설이라고 하면, 바로 그 추정치를 해당 모집단에 관한 가장 적절한 추정치로서 선호할 수 있다는 것이다. 피셔에 있어 이와같은 원리를 이른 바 "최대우도의 원리 (Principle of Maximum Likelihood)" 라 부르며, 이와같은 원리에 따라 어떤 모수에 관한 가장 적절한 추정치 (Estimate) 를 구하는 방법을 이른 바 "최대우도의 방법 (Method of Maximum Likelihood) 이라 부른다.
주어진 데이터만으로 미지의 최적 모델 파라미터 θ를 찾아야 한다. 입력값 X와 파라미터 θ가 주어졌을 때 정답 Y가 나타날 확률, 즉 우도 P(Y|X; θ)가 바로 우리가 찾고싶은 결과이다.
Negative Log-likelihood(음의 로그 우도) : 딥러닝 모델의 손실함수로 음의 로그 우도가 쓰인다.

위 식에서 f는 범주 수만큼의 차원을 갖는 벡터로써 unnormalized log probabilities에 해당한다. 정답 인덱스에 해당하는 f의 요소값을 높인다는 말은 우도를 높인다(=입력값 X를 넣었을 때 Y 관련 스코어를 높인다)는 의미로 해석할 수 있다.
Cross Entropy : 두 확률분포 p와 q 사이의 차이를 계산하는데에 쓰이는 함수
-∑p(x) log q(x) 이다.
p는 우리가 가진 데이터의 분포 P(Y|X), q는 모델이 예측한결과의 분포 P(Y|X; θ)로 둔다.
그러면 크로스 엔트로피는 파라미터θ 하에서의 음의 로그우도의 기대값이라고 해석할 수 있다.
따라서 -∑P(Y|X) log P(Y|X; θ)를 최소화 하는 θ가 우리가 찾고 싶은 모델이 된다.
우도의 곱이 최대인 모델을 찾는 것은 로그우도의 기대값이 최대인 모델을 찾는 것과 같으며, 또한 학습데이터의 분포와 모델이 예측한 결과의 분포 사이의 차이, 즉 크로스 엔트로피를 최소화하는 것과 같다. 이 때문에 Negative Log-likehood가 딥러닝의 손실함수가 되는 것입니다.
Cross Entropy 계산 예시

범주가 2개이고 정답 레이블이 [1,0]인 관측치 x가 있다고 치면 P는 우리가 가지고 있는 데이터의 분포를 나타내므로 첫번째 범주일 확률이 1, 두번째 범주일 확률은 0이라고 해석할 수 있다.
P는 우리가 가지고 있는 데이터의 분포를 나타내므로 첫번째 범주일 확률이 1, 두번째 범주일 확률은 0이라고 해석할 수 있다.
Q는 P에 근사하도록 만들고 싶은, 딥러닝 학습 대상 분포이다.
그런데 모델 학습이 잘 안돼서 Q가 [0,1]T 로 나왔다면 loss는 무한대로 치솟게 된다.

이번엔 학습이 잘돼서 모델이 정답과 일치하는 [1,0]을 예측했다고 하면 loss는 다음과 같이 0이 된다.

여기서 0log0은 0으로 취급한다.
손실함수로 Negative Log-likelihood를 쓰면 몇가지 이점이 생긴다. 우리가 만드려는 모델에 다양한 확률분포를 가정할 수 있게 돼 유연하게 대응할 수 있게 된다. Negative Log-likelihood로 딥러닝 모델의 손실을 정의하면 이는 곧 두 확률분포 사이의 차이를 재는 함수인 크로스 엔트로피가 되며, 크로스 엔트로피는 비교 대상 확률분포의 종류를 특정하지 않기 때문이다.
이는 평균제곱오차(Mean Squared Error)의 최소화와 본질적으로 동일하다.
다시말하면 각각의 확률분포에 맞는 손실을 따로 정의할 필요가 없이 Negative Log-likelihood만 써도 되고, output node의 종류만 바꾸면 세 개의 확률분포에 대응할 수 있게 된다는 이야기이다.
weight decay regularization :
'📌 Paper > Deepsurv' 카테고리의 다른 글
| 카플란 마이어 생존분석 (0) | 2021.03.11 |
|---|---|
| Deepsurv - 실행 과정 (0) | 2021.01.20 |
| 생존 함수, Cox hazard model (0) | 2021.01.11 |
| Deepsurv 논문 읽기 (0) | 2021.01.11 |
| Tensorflow - Theano - Torch - Keras - Lasagne (0) | 2021.01.04 |