결정론적 튜링기계 : 한 방향으로 문제를 해결하는 기계
다항시간 : 다항식으로 표현될 수 있는 시간.
다항식안의 미지수 : 알고리즘의 입력 크기
4 2 3 1
-> 2 4 3 1
-> 2 3 4 1
-> 2 3 1 4
-> 2 3 1 4
-> 2 1 3 4
-> 2 1 3 4
-> 1 2 3 4
(n-1) + (n-2) + .. + 1 = (n-1)(n)/2
주어지는 숫자의 개수 : 입력 크기
P 문제 : 알고리즘 속도가 다항식으로 표현되는 문제들 (Polynomial) , 쉬운 문제
NP 문제 : 다항식으로 표현될 수 있는지 여부가 알려지지 않은 문제들 (Non-deterministic Polynomial), 어려운 문제
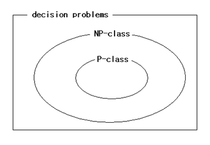
결정형 문제
결정형 문제(decision problem)란 그 답이 'yes’와 ‘no’ 둘 중의 하나로 결정되는 문제를 뜻한다.
P와 NP는 결정형 문제에 한해서 정의된다.
이와 대조되는 개념으로 답에 셋 이상의 경우의 수가 있는 문제를 함수형 문제(function problem)라고 한다.
어떤 결정형 문제에 대해 유한한 시간 내에 답이 '예’인 경우와 '아니오’인 경우 모두를 답할 수 있으면 그 문제는 결정 가능하다(decidable)라고 한다.
결정성 알고리즘
결정성 알고리즘(deterministic algorithm)은 각 단계에서 그 다음 단계가 유일하게 결정되는 알고리즘을 말한다.
우리가 여러 프로그래밍 언어로 작성하는 코드는 모두 결정성 알고리즘에 의한 것이다.
비결정성 알고리즘
비결정성 알고리즘(non-deterministic algorithm)은 '각 단계에서 그 다음 단계가 유일하게 결정되지 않는 알고리즘’을 말한다.
Non-deterministic Algorithm : Guessing(찍고) 후 Verification(확인) 하는 알고리즘
Verification Stage에서 True 혹은 False 로 나온다.
P 문제 : 알고리즘 속도가 다항식으로 표현되는 문제들 (Polynomial) , 쉬운 문제
다항식 시간에 Yes 또는 No 대답을 할 수 있으면 P
df) P = set of decision problems that can be solved in polynomial step of the input bit size by a TM
P is the set of all decision problems that can be solved by polynomial-time algorithms.
P 문제 : (결정론적) 튜링 기계로 다항식 시간 내에 해결 가능한 문제
즉 빅오 표기법으로 표현하면 해결 시간이 다항식 꼴이 나오는 문제이다.
P 문제는 결정성 알고리즘으로 다항식 시간 내에 해결 가능한결정형 문제이다.
P is similar to a problem that a normal people can find its solution easily.
P : 어떤 문제의 해답을 빠른 시간(=다항 함수)안에 찾을 수 있는 문제.
다항 함수 : 한 변수의 곱셉과 덧셈으로만 이루어진 식. (3+2x2+5x3)
NP 문제 : 다항식으로 표현될 수 있는지 여부가 알려지지 않은 문제들 (Nondeterministic Polynomial), 어려운 문제
Yes 대답이 나오는 해를 제공했을 때, 이것이 Yes 대답을 내는 해라는 사실을 다항식 시간에 확인해줄 수 있으면 NP
df) NP = set of all decision problems for which any yes instance has some 'proof' that verifies the problem to be yes in polynomial step
(다른정의: NP = set of decision problems that can't be solved in polynomial step by a Nondeterministic algorithms)
NP 문제 : (다항식 시간 안에 해결 가능한지는 모르겠지만, 입력한 답이 맞을 경우) 맞다는 것을 다항식 시간 내에 증명 가능한 문제.
이는 "'비결정론적 튜링 기계’로 다항식 시간 내에 해결 가능한 문제"라고도 한다.(무수히 많은 튜링 기계를 병렬로 묶은 다음 가능한 모든 경우를 넣으면 다항식 시간 후에 그 중 하나가 정답을 알아내게 되기 때문이다.)
NP 문제는 비결정성 알고리즘으로 다항식 시간 내에 해결 가능한 결정형 문제이다.
NP is a problem that a normal people can grade whether other person’s solution is correct or not easily.
NP : 어떤 문제에 대해 내가 제시한 답이 정답인지 아닌지만 빠른 시간안에 O, X로 판단 할 수 있는 문제. (따라서 정답을 찾는 데 매우 오랜 시간이 걸린다. 어떤 문제를 빠른 시간 안에 풀 수 있는 알고리즘이 존재한다고 증명되기만 해도 P문제에 속한다.)
P ⊆ NP 인지는 아무도 모른다.


P의 input = x
Q의 input = Transformation function 의 output
P, Q중 어느게 더 어려운 문제일까? : Q
Problem P is reducible to Q
NP클래스 안에 있는 모든 문제가 어떤 문제 Q로 reducible 하면, 그 문제 Q는 NP-Hard이다.
Q를 풀 수 있는 알고리즘으로 NP클래스에 있는 모든 문제를 풀 수 있다.
간단히 말해, NP 클래스 안에 있는 모든 문제들보다 Q가 "어렵다"고 할 수 있다. (어렵거나 같다)
NP-Hard이면서 NP클래스 안에 있으면 NP-Complete이다.
[공유] 알고리즘 용어
알고리즘 자료 모음어떤 수학적인 문제problem를 유한한 단계 안에 해결하기 위한 방법 혹은 절차를 알고리...
blog.naver.com
NP 문제란?
비결정론적 튜링기계를 사용하여 다항시간 내에 답을 구할 수 있는 문제.
여러개의 선택지가 있는 것이 특징이다.
{-2, 10, 6, -5, -3} 중 합이 0인 것 찾기
{-2, 10, -5, -3}
이 숫자 조합을 찾아내는 과정은 무작위로 계산하는 과정을 거쳤을 것이다.
하나의 선택지가 아닌 여러개의 선택지, 즉 운에 의해 푸는 기계 : 비결정론적 튜링기계
2^5
NP에 속한 문제들이 궁극적으로 다항식, 즉 쉬운 알고리즘을 이용해서 해결될 수 있을까? 라는 질문이 중요하다.
만약 그렇다면 P=NP 라는 등식이 성립하게 될 것이다.
하지만 NP에 속한 문제가 모두 다항식으로 해결될 수 있을지 여부를 파악하거나 증명하는 것이 너무나 어렵다.
NP-hard 와 NP-complete
1) NP-hard
모든 경우의 수를 전부 확인해보는 방법 이외에는 정확한 답을 구할 수 있는 뾰족한 수가 없는 "문제"들
2) NP-complete
NP-hard(모든 경우의 수 확인) 문제이면서 동시에 NP(시간이 얼마나 걸릴지 모름) "문제"들

B를 다항식 시간안에 풀 수 있다면, NP에 속하는 모든 다른 문제도 다항식 시간에 풀 수 있다.
B가 NP에 속한 문제중에서 가장 어렵다.
NP-완전(NP-complete, NP-C) 문제 :
'NP 집합에 속하는 결정 문제 중에서 가장 어려운 문제의 부분집합’으로, NP와 NP-난해의 교집합이 NP-완전임이 알려져 있다. 모든 NP 문제를 다항 시간 내에 NP-완전 문제로 환원할 수 있으므로 NP-완전 문제 중 하나라도 P에 속한다는 것을 증명한다면 모든 NP 문제가 P에 속하기 때문에, P-NP 문제가 P=NP의 형태로 풀리게 된다. 반대로 NP-완전 문제 중의 하나가 P에 속하지 않는다는 것이 증명된다면 P=NP에 대한 반례가 되어 P-NP 문제는 P≠NP의 형태로 풀리게 된다.
NP-Complete : NP이면서 NP-Hard인 문제. 즉 모든 NP 문제들이 이 'NP문제’로 Reduction이 가능할 때.
(어떤 NP 문제가 다항함수 시간안에 NP-Complete으로 Reduction이 가능한 경우, 그 문제도 역시 NP-Complete임이 증명되어있다. 그래서 1개의 NP-Complete이 발견된 이후 많은 문제들이 그 문제를 통해 Reduction 되어 NP-Complete임을 증명했다.)

isomerphic problem : NP이지만 P도 아니고 NP-complete도 아닌 문제
NP complete가 NP 문제중 가장 어려운 문제인데
NP complete가 다항식 시간 내에 풀리면, NP 문제는 모두 다항식 시간 내에 풀리고
NP 문제가 모두 다항식 시간 내에 풀린다면, NP 문제는 모두 P 에 속하게 된다. NP 문제가 다항식 시간 알고리즘이 있다.
그러면 NP ⊆ P 가 된다.
그러면 P = NP가 된다. (원래 P ⊆ NP 였으므로)
ex)
문제 A : n개의 숫자를 작은 순서부터 오른차순 정렬
문제 B : n개의 숫자 중에 가장 작은 숫자를 찾는 문제
문제 C : n개의 숫자 중에 가장 큰 숫자를 찾는 문제
문제 D : n개의 숫자 중에 중간값을 찾는 문제
B C D는 A로도 환원이 가능하다.
다항시간내에 풀이가 될 수 있다면, 즉 모든 NP 문제들이 P 문제가 될 수 있다면, 모든 NP문제들을 결정론적 튜링기계를 이용하여 풀이가 다항시간내에 가능하게 된다.
NP-완전문제는 해결 가능하다고 판명남
NP-난해문제는 해결 가능하다고 판명이 나지 않음
P NP 문제란?
P문제의 집합과 NP-완전문제의 집합이 서로 같은 집합이냐, 다른 집합이냐를 묻는 문제

대다수의 학자들은 P != NP 일 것이라고 예상
P=NP 일 경우 거의 모든 암호는 안전할 수 없게 됨
알고리즘 과제 #7
2020. 6. 19
● 1. [10점] 많은 NP-complete 문제들 중에서 아무 문제 하나에 대해서 다항식 시간 알고리즘이 발견되는 사건이 일어났다고 가정하자. 그러면 이 사건은class(집합) P와 class(집합) NP가 같은 집합이라는 것 (P = NP)을 의미한다. 왜 그런지 증명하시오.
Solution :
NP-Complete의 Definition은 다음과 같다. 문제 B가 NP-complete일 때 B라는 문제를 풀 수 있는 다항식 시간 알고리즘이 존재한다면, NP에 속하는 임의의 문제에 대하여 다항식 시간 알고리즘이 존재한다. P는 NP에 속하고, B라는 문제 하나에 대해 다항식 시간 알고리즘이 발견된다면 NP에 속한 모든 문제를 다항식 시간에 풀 수 있으므로 NP는 P에 속하게되고, 결과적으로 P=NP 이게 된다.
● 2. [10점] 많은 NP-complete 문제들 중에서 아무 문제 하나에 대해서 그 문제는 다항식 시간 알고리즘이 존재할 수 없다고 증명되는 사건이 일어났다고 가정하자. 그러면 이 사건은 class(집합) P와 class(집합) NP가 다른 집합이라는 것 (P ≠ NP)을 의미한다. 왜 그런지 증명하시오.
Solution :
NP-Complete의 Definition은 다음과 같다. 문제 B가 NP-complete일 때 B라는 문제를 풀 수 있는 다항식 시간 알고리즘이 존재한다면, NP에 속하는 임의의 문제에 대하여 다항식 시간 알고리즘이 존재한다. P는 NP에 속하고, B라는 문제 하나에 대해 다항식 시간 알고리즘이 존재할 수 없다고 증명된다면, NP에 속한 모든 문제를 다항식 시간에 풀 수 없으므로 NP는 P에 속하지 않게 되고, 결과적으로 P≠NP 이게 된다.
● 3. [10점] 문제 A와 문제 B가 둘 다 NP-complete 문제라고 하자. 그러면 문제 A가 문제 B로 다항식시간 환원가능 하고 (problem A is polynomial-time reducible to problem B), 또한 문제 B가 문제 A로 다항식시간 환원가능 하다(problem B is polynomial-time reducible to problem A). 왜 그런지 증명하시오.
Solution :
NP-Complete Definition를 problem B에 적용해보면
어떠한 problem B에 대해서,
1. B는 NP이고,
2. NP의 모든 문제 A에 대해서 A∝B이다.
그러면 B는 NP-complete이다 라는 것을 알 수 있다.
NP-Complete Definition를 problem A에 적용해보면
어떠한 problem A에 대해서,
1. A는 NP이고,
2. NP의 모든 문제 B에 대해서 B∝A이다.
그러면 A는 NP-complete이다 라는 것을 알 수 있다.
따라서 A는 B로 reducible 할 수 있고, B는 A로 reducible 할 수 있다.
◐ 4. [10점] Traveling Salesperson Decision Problem의 polynomial-time verification algorithm의 pseudocode를 작성하고, 시간복잡도를 분석하여 big-Θ 기호로 나타내시오. Verification algorithm의 function header는 교재의 407쪽에 있는 것을 사용하고, guess string S는 방문하는 vertex의 번호들로 이루어진 배열이라고 가정하시오.
(G,d) G라는 그래프에 d라는 integer 값을 도입해서 d보다 작은 투어가 존재하는가 존재하지 않는가? 로 만든다.
내책 503p
Solution :
Write the pseudocode of the polynomial-time verification algorithm of Traveling Salesperson Decision Problem, analyze the time complexity and mark it with the big-Θ symbol. Assume that the function header of Verification algorithm uses the one on page 407 of the textbook, and the Guess String S is an array of numbers from vertex to visit.
● 5. [10점] 교재의 제 421 쪽의 Figure 9.8에 있는 두 그래프는 isomorphic 이다. 두 그래프의 정점(vertex)들을 어떻게 일대일 대응 시켰을 경우에 isomorphic 이라는 것을 알 수 있는지, 그 일대일 대응을 쓰시오. 다시 말해서, 왼쪽 그래프의 각 정점 에 대해서 오른쪽 그래프의 어느 정점을 대응시켜야하는지 쓰시오.
Solution :
v1 - u5
v2 - u3
v3 - u1
v4 - u4
v5 - u2
● 6. [10점] Undirected graph G의 두 개의 정점 u, v에 관한 해밀토니안 경로(hamiltonain path)란 u와 v를 연결하는 경로(path)로서 그래프 G의 모든 정점을 꼭 한 번씩 지나가는 경로를 말한다. Hamiltonian path는 모든 정점을 꼭 한 번씩 지나간다는 면에서는 Hamiltonian cycle과 유사한 개념이지만, cycle이 아니라 시작점과 끝점이 다르다. Hamiltonian path problem이란 주어진 (G, u, v)에 대해서 u와 v를 잇는 Hamiltonian path가 존재하는지 결정하는 문제이다. Hamiltonian path problem은 NP-complete problem임이 증명되어 있다.
Longest path problem이란 주어진 weighted undirected graph G, 두 정점 u, v, 그리고 정수 k (G, u, v, k)에 대해서, u와 v를 잇는 경로로서 그 가중치(weight)가 k 보다 크거나 같은 경로가 존재하는지 결정하는 문제이다.
Hamiltonian path problem이 Longest path problem으로 다항식시간 환원가능 (polynomial-time reducible)함을 증명하시오.
Solution :
먼저 해밀턴 경로 문제가 NP-complete problem임이 증명되어 있다. NP-Complete Definition를 Hemilton Cycle에 적용해보자. undirected G = (V, E)에 의해 G가 Hamiltonain path를 포함하는지 알 수 있다. (Hamiltonian path는 모든 꼭지점을 한번만 방문한다.)
그러면 Hamiltonian Path가 NP인지 확인할 수 있다. 따라서 HamiltonianCycle ∝ HamiltonPath를 알 수 있다.
Hamiltonian Cycle의 인스턴스 G = (V, E)가 있다고 하자.
모든 edge인 e = {u, v} 가 G의 E에 포함되어있고, u와 v에 연결된 u', v'을 추가한 Ge를 만들 수 있다.
Ge = (V ∪ {u′, v′}, E ∪ {u′, u} ∪ {v′, v}).
이는 모든 edge에 대해서 e ∈ E 가 적용된다.
edge e 를 사용하는 G의 Hamiltonian cycle 이 존재할때만 Ge의 Hamiltonian path가 존재한다.
그러므로 G의 Hamiltonian cucle이 존재할 때만 Hmailtonian path의 Ge가 어떤 edge에 대해서 e ∈ E 이다.
이 reduction은 polynomial time이 소요된다.
따라서 G의 Hamiltonian path가 path의 길이가 n-1일때를 확인함으로써 Longest Path는 NP이고 HamiltonianPath ∝ LongestPath 를 알 수 있고 Hamiltonian path가 Longest path 로 다항식시간 환원가능 (polynomial-time reducible)함을 알 수 있다.
7. [20점] Undirected graph의 vertex cover란 정점들의 집합 S로서 그래프의 모든 에지들을 cover하는 집합을 말한다. 다시 말해서, 그래프의 임의의에지 e = (u, v)의 양 끝점 u, v 중에서 적어도 하나는 집합 S에 속한다. 예를 들어서, 교재의 제 405쪽 Figure 9.1의 그래프에서 는 vertex cover이다. 그러나 는 vertex cover가 아니다, 왜냐하면 에지 가 cover 되지 않기 때문이다.
Vertex cover problem이란 주어진 undirected graph G와 정수 k (G, k)에 대해서 그래프 G에 크기(size)가 k 보다 작거나 같은 vertex cover가 존재하는지 결정하는 문제이다. Vertex cover의 size란 vertex cover의 원소의 개수를 뜻한다. 예를 들어서, 의 size는 3이다. Vertex cover problem은 NP-complete problem임이 증명되어 있다.
Clique decision problem이 vertex cover problem으로 다항식시간 환원가능 (polynomial-time reducible)함을 증명하시오.
The vertex cover of an undirected graph is a set of vertexes that cover all the edges of the graph as S. In other words, at least one of the two end points u, v, of any edge e = (u, v) on the graph belongs to the set S. For example, in the graph in Figure 9.1 on page 405 of the textbook is vertex cover. But is not a vertex cover, because the edge is not covered.
Vertex cover problem is a matter of determining whether a vertex cover exists in graph G, size less than or equal to k, for a given undirected graph G and integer k (G, k). The size of a vertex cover is the number of elements of a vertex cover. For example, size of is 3. Vertex cover problem proved NP-completion problem.
Prove the polynomial-time returnable with vertex cover problem.
● 8. [20점] Conjunctive normal form (CNF)의 각 clause가 꼭 3 개의 literal로 이루어지면 3-CNF라고 부른다. 예를 들어서,

는 3-CNF 이다. 임의의 3-CNF가 satisfiable인지 결정하는 문제를 3-Satisfiability problem이라고 한다. 3-Satisfiability problem은 NP-complete problem임이 증명되어 있다.
임의의 undirected graph가 3가지 색깔로 칠하는 것이 (인접한 정점들을 다른 색으로 칠하는 것이) 가능한지 결정하는 문제를 3-coloring problem이라고 한다.
3-satisfiability problem이 3-coloring problem으로 다항식시간 환원가능 (polynomial-time reducible)함을 증명하시오.
[Hint: 3-satisfiability problem을 3-coloring problem으로 transform할 때 아래와 같은 부분 그래프를 만들어 사용하는 것이 도움이 될 수 있음.]
Solution :
3-satisfiability problem이 3-coloring problem으로 다항식시간 환원가능 (polynomial-time reducible)함을 증명하기 위해 {T,F,B} 의 정점을 갖는 그래프를 이용한다. T=True, F=False, B=Base . G는 3-Coloring의 인스턴스라고 하자. 3-SAT의 인스턴스는 S라고 하자.
{T,F,B}을(를) G의 꼭지점에 색칠하는 데 사용할 색상 집합으로 생각해 보면, 이 삼각형은 G의 일부분이므로, 우리는 이미 G의 색상에 3가지 색상이 필요하다. 다음에는 모든 리터럴 xi에 대해 vi, 두 개의 꼭지점 vi를 추가하고 (vi, vi) 쌍에 대해 다음과 같이 삼각형 B, vi를 생성한다.
Ci = (a ∨ b ∨ c) 인 절의 경우, {T, F, B} 색상을 사용하여 리터럴의 OR을 표현해야 한다. 아래와 같이 표현한다.

이 그래프는 Output 노드에 (a ∨ b ∨ c)이 붙은 회로라고 생각할 수 있다. 우리는 Ci가 만족하면 이 노드가 T, 그렇지 않으면 F가 되기를 원한다. 이 과정은 두 단계로 구성된다. (a ∨ b) 인 노드는 (a ∨ b)를 하고 우리는 (a ∨ b) ∨ c)에 대해 동일한 작업을 반복한다.
만약 a, b, c가 모두 3-coloring인 경우, OR-gadget의 출력 노드는 F색이어야 한다. 따라서 Ci = (a ∨ b ∨ c) 는 unsatisfy 하다.
만약 a, b, c 중 하나가 컬러 T인 경우 출력 노드가 컬러 T인 OR-gadget의 유효한 3컬러가 존재한다. 따라서 Ci = (a ∨ b ∨ c) 는 satisfy 하다.
3-SAT의 인스턴스 S 에서 모든 Ci의 OR-gadget을 추가하면 다음과 같이 연결한다.

이를 통해 3-SAT 의 인스턴스 S가 위의 그래프의 3-Coloring 의 인스턴스 G로 이라면 만족하다는 것을 확인할 수 있다.
따라서 3-Coloring problem은 NP이고 3-satisfiability problem이 3-coloring problem으로 다항식시간 환원가능 (polynomial-time reducible)함을 확인할 수 있다.
● 9. [20점] 현재로서는 graph isomorphism problem이 P에 속하는지 또는 NP-complete 인지 아무도 정확히 알지 못한다. 아래의 각 소문제에 대하여 답하고, 그렇게 답한 이유를 쓰시오.
(1) 만약 graph isomorphism problem 에 대한 다항식 알고리즘이 발견되는 사건이 일어난다면, 이것은 P = NP 라는 것을 의미하는가? P ≠ NP 라는 것을 의미하는가? P vs NP 의 해결에 대한 아무런 도움이 되지 못하는가?
Solution : P = NP
왜냐하면 graph isomorphsim problem은 P나 NP-complete 이지 않기 때문에 NP이다;
만약 P 시간 안에 그것을 푸는 알고리즘이 존재한다면, NP는 P가 된다;
(2) 만약 graph isomorphism problem 이 NP-complete 임이 증명되는 사건이 일어난다면, 이것은 P = NP 라는 것을 의미하는가? P ≠ NP 라는 것을 의미하는가? P vs NP 의 해결에 대한 아무런 도움이 되지 못하는가?
Solution : P ≠ NP
graph isomorphism problem이 NP-complete 임이 증명되는 사건이 일어난다면, NP=NP-complete 이다.
처음에 Graph-Isomorphic은 NP라고 주어지기 때문이다.
(3) 만약 graph isomorphism problem 이 다항식시간 알고리즘이 존재하지 않는다는 사실이 증명되는 사건이 일어난다면, 이것은 P = NP 라는 것을 의미하는가? P ≠ NP 라는 것을 의미하는가? P vs. NP 의 해결에 대한 아무런 도움이 되지 못하는가?
Solution : P ≠ NP
만약 graph isomorphism problem 이 다항식시간 알고리즘이 존재하지 않는다는 사실이 증명되는 사건이 일어난다면, P ≠ NP이다. 초기에 NP problem 이라고 주어지기 때문이다.
(4) 만약 graph isomorphism problem 이 다항식시간 알고리즘이 존재하지 않는다는 사실이 증명되는 사건이 일어난다면, 이것은 graph isomorphism problem이 NP-complete problem이라는 것을 의미하는가?
Solution : NP-complete problem이 아니다.
만약graph isomorphism problem이 다항식 시간 알고리즘이 존재하지 않는다는 사실이 증명되는 사건이 일어난다면, 그것은 그것이 다른 NP 클래스 문제에서 해결될 수 있다는 것을 의미하므로, NP-Hard 라는 것을 의미한다.
10. [10점] 교재 제 425쪽에 NP-easy의 정의(definition)가 있다. 그 정의를 Def1 이라고 하자. 다음은 NP-easy의 다른 정의이다: A problem A is called NP-easy if, for some NP-complete problem B, . 이 정의를 Def2 라고 하자.
Def1과 Def2가 동등함을 증명하시오. 다시 말해서, 문제 A가 Def1에 의해서 NP-easy이면 Def2에 의해서도 NP-easy임을 보이고, 또한 문제 A가 Def2에 의해서 NP-easy이면 Def1에 의해서도 NP-easy임을 보여야 함.
11. [10점] 교재의 Example 9.17는 Traveling Salesperson Optimization problem(TSPopt)가 Traveling Salesperson Extension Decision problem(TSPext)로 polynomial-time Turing reducible임을 증명하고 있다. 이 증명을 보면 mindist 값을 구하기 위해서 dmin과 dmax 사이에서binary search를 하고 있다.
만약 mindist 값을 구하기 위해서 dmin과 dmax 사이에서 linear search(sequential search; 선형탐색)를 한다면, 그 증명은 틀린 증명이다. 왜 틀린증명인지 그 이유를 쓰시오.
◐ 12. [10점] 교재의 제 430 쪽에 TSP with triangular inequality 문제의 approximation algorithm이 나와 있다. 세 부분으로 이루어진 이 알고리즘의 각부분의 시간복잡도를 분석하여 big-Θ 기호로 나타내고, 또한 전체 알고리즘의 시간복잡도도 big-Θ 기호로 나타내시오.
'🕶 Algorithm > 알고리즘' 카테고리의 다른 글
| 선택 정렬 (Select sort) (0) | 2021.07.21 |
|---|---|
| 버블 정렬 (Bubble sort) (0) | 2021.07.21 |
| Backtracking (0) | 2020.06.08 |
| Greedy Algorithm (0) | 2020.05.18 |
| Greedy Approach - Prim's Algorithm (0) | 2020.05.18 |