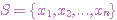
동적 프로그래밍과 함께 최적화 문제의 해결에 많이 사용된다.
문제 해결을 위해 데이터를 선택할 때, 그 순간에 가장 최고인 것을 선택한다.
지역적으로는 최적이지만 전체적인 최적은 확신할 수 없다.
알고리즘이 항상 최적해를 주는지 확인이 필요하다.
Greedy Algorithm 적용 단계
- 선택 과정(Selction procdure) : 현재 상태에서 최선인 답을 찾아 해답에 포함한다.
- 적정성 검사(Feasibilty check) : 새로 결정된 해답들이 적정한지 검사한다.
- 해답 점검(Solution check) : 새로 얻은 해답들이 최적인지 검사한다.
배낭 문제 (Knapsack Problem)
n개의 물건과 배낭이 있다고 가정하자.
각각의 물건에는 무게와 가치가 주어진다.
배낭에 물건을 넣을 때, 그 배낭이 견딜 수 있는 최대 하중이 W라고 가정하자.
목표
: 배낭에 넣을 수 있는 물건의 가치를 최대화하면서 최대 하중 W를 초과하지 않도록 한다.
문제의 정의
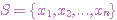
Wi = 물건 Xi 의 무게
Pi = 물건 Xi 의 가치
A ⊂ S = 물건들의 집합 A가 S의 부분집합이라고 가정하자

: 배낭문제의 목표 함수
최소비용 신장트리(Minimum Spanning Tree)
가중 그래프
: 연결선에 가중치를 부여한 그래프로써 네트워크 라고도 한다.
가중 그래프의 예
: 각 vertex들을 도시라 하고 edge들은 그 도시를 잇는 도로라 했을 때, edge에 할당된 가중치는 각 도로에 대한 교툥량이나 또한 도시 사이의 거리라고 생각할 수 있다.

신장 트리의 비용
: 가중 그래프로부터 신장 트리를 생성하여 그 신장 트리를 구성하는 모든 연결선들의 가중치를 합한 값
최소 비용 신장 트리
: 모든 신장 트리들 중에 최소비용을 가진 신장 트리
최소 비용 신장트리를 생성하는 알고리즘
: Prim, Kruskal 알고리즘
Prim's 알고리즘
전체 연결선 중에서 가장 작은 가중치를 갖는 연결선을 선택하여 최소비용신장트리에 추가시키고
정점들은 정점들의 집합 V에 추가
다음은 V에 속한 정점들과 인접한 연결선들 중 가장 작은 가중치를 갖는 연결선을 MST에 추가하고
정점 또한 집합 V에 추가
이러한 과정을 신장트리의 연결선 개수가 n-1이 될때까지 반복

float Prim(int E[][size], float cost[][size], int n, int t[][2])
{
int near[size],j,k,l;
let (k,l) be an edge of minimum cost in E;
float mincost = cost[k][l]; t[1][1] = k; t[1][2] = 1;
for (int i=1; i < = n ; i++) //initialization
if (cost[i][1] < cost[i][k]) near[i] = 1;
else near[i] =k;
near[k] = near[1] = 0;
for (i=2; i< = n-1 ; I++) {
let j be an index such that near[j]!=0 and
cost[j]near[j] is minimum; t[i][1] = j; t[i][2] = near[j];
mincost = mincost + cost[j][near[j]]; near[j] = 0;
for (k=1; k < = n ; k++)
if ((near[k] != 0) && (cost[k][near[k[] > cost[k][j]))
near[k] = j;
}
return(mincost);
}
'🕶 Algorithm > 알고리즘' 카테고리의 다른 글
| NP hard (0) | 2020.06.21 |
|---|---|
| Backtracking (0) | 2020.06.08 |
| Greedy Approach - Prim's Algorithm (0) | 2020.05.18 |
| Sequence Alignment Algorithm (0) | 2020.05.15 |
| Traveling Salesperson Problem (0) | 2020.05.14 |