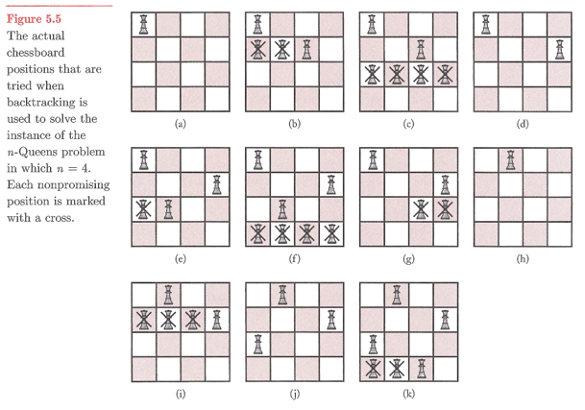

체스판을 대각선 방향으로 놓지 않도록 모든 행마다 하나씩 놓는다.
앞으로 가다가 막히면 옆으로 가고 옆에도 막혀있으면 뒤로가는 방법.
(2,4,1,3) 으로 표현할 수 있다.
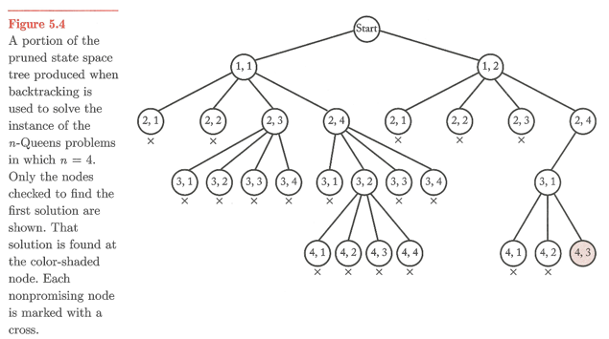
트리 형태로 Backtracking(퇴각검색)을 설명할 수도 있다.
다 놓아보고 찾는게 아니라
하나씩 놓으면서 우회하는 방법이므로 시간을 절약할 수 있다.
Pruning(가지치기) 라고도 한다.

v = 스타트 노드
recursion으로 한다.


queens를 recursion 한다.
위에서 배운 tree를 만드는 것은 아니다.
column 이라는 그저 길이 4짜리 배열을 하나 만든다.
(a) 1 / / /
(b) 1 / 3 / /
(c) 1 / 3 / x / x
(d) 1 / 4 / /
(e) 1 / 4 / 2 /
promising(i) = i 까지 Queen이 대각선으로 겹치지 않는다.
i 가 n번째 까지 했으면 반환하고 그렇지 않으면 recursion 한다.

promising 함수는 대각선에 걸리냐 걸리지 않느냐를 확인하는 함수이다.
column에 i번째 까지 들어가 있다.
k가 1부터 i 까지 변하는 동안에 if 조건에 걸리면 안된다.
col[i] == col[k] // 앞에 있던 column number와 같은게 있으면 안된다.
abs(col[i] - col[k]) == i - k // i와 k의 difference가 column number의 difference와 같으면 안된다. = 대각선에 걸리면 안된다.

#include<stdio.h>
#include <stdbool.h>
int n;
int col[13];
int cnt, promising_node, sol;
bool first;
bool promising(int i);
void queens(int i);
void main() {
int i;
first = true;
scanf("%d", &n);
queens(0);
if (sol != 0)printf("%d %d %d", cnt, promising_node, sol);
else printf("No solution");
}
bool promising(int i) {
int k = 1;
bool s = true;
cnt++;
while (k < i && s ) {
if (col[i] == col[k] || col[i] - col[k] == i - k|| col[k] - col[i] == i - k) {
s = false;
}
k++;
}
return s;
}
void queens(int i) {
int j;
if (promising(i)) {
promising_node++;
if (i == n) {
sol++;
if (first) {
for (int j = 1; j <= n; j++) {
printf("%d ", col[j]);
}
first = false;
}
}
else {
for (j = 1; j <= n; j++) {
col[i + 1] = j;
queens(i + 1);
}
}
}
}
'🕶 Algorithm > 알고리즘' 카테고리의 다른 글
| 버블 정렬 (Bubble sort) (0) | 2021.07.21 |
|---|---|
| NP hard (0) | 2020.06.21 |
| Greedy Algorithm (0) | 2020.05.18 |
| Greedy Approach - Prim's Algorithm (0) | 2020.05.18 |
| Sequence Alignment Algorithm (0) | 2020.05.15 |