최소제곱법은 자료들 사이에서 패턴을 도출해내는데 쓰인다.
아주 직관적이고 간단하기 때문에, 수치해석, 회귀분석 등 다양한 통계학적 접근의 기본이 된다.
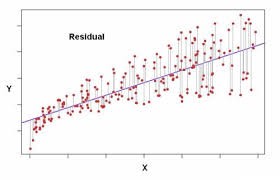
다음 그래프를 보자, 각 자료가 흩뿌려져 있는데, 이 점 들 사이에 일관성을 찾기 위해 그래프 f(x)를 도출한다고 가정하자.
각 점들과 그래프 간의 차이를 residual이라고 한다.
그래프는 가장 오차가 적어야 한다.
오차가 적어야 하다는 것은 각 점들과 그래프 간의 오차가 가장 최소가 되는 f(x)를 찾아야한다는 것을 의미한다.

수식으로 나타내면 아래와 같다.
변수 x와 상수 B가 주어졌을 때, 식은 다음과 같다.
f(x)는 선형인 일차 함수로 가정을 한다.
x와 y는 주어지는 값이니, residual의 최소값은 기울기 a와 절편 b로 결정된다.
각 점들에서 가장 가까운 1차 함수 그래프의 식을 구하는 것이 최소제곱법의 목적이다.

Residual 합의 최소값이 되는 a,b는 a 와 b 를 편미분하여서 도출이된다.
페르마의 정리에 의해 미분값이 0이 도출이 되는 값이 임계점이 되기 때문이다.
각각의 편미분 값이 0인 a, b의 식을 연립방정식으로 계산한다.

위 식을 풀어서 계산을 해보자.

식을 정리한 다음 a,b로 편미분을 해보자.

여기서 복잡한 계산이 수행되는데, 실제로는 residual²의 최소값을 구하는데 행렬을 이용한 계산을한다. 위의 식을 행렬로 표시하면 다음과 같다. AX=B라고 할때, X = A⁻¹*B이다.

최소제곱법의 적용 사례
최소제곱법은 다양한 방법에서 활용할 수 있다. 다음의 영지 짜장면 집에서 짜장면 가격이 오르면 얼마나 손님이 줄어드는지에 관한 표이다. 여기서 최소제곱법을 통해서 가격과 손님간의 상관함수를 도출할 수 있다.

앞선 행렬을 여기 대입을 해보면 다음과 같다.

위 식을 풀어서 계산을 하면 다음과 같다. Residual² 가 최소가 되는 방정식은 f(x)는 -0.25x+ 18이다.

'✏️ Mathemathics > Statistics and Probability' 카테고리의 다른 글
| 단순 선형 회귀분석 - 회귀식 추정 및 결정계수 (0) | 2020.04.09 |
|---|---|
| 3주차 과제 (0) | 2020.04.02 |
| p-value (0) | 2020.03.23 |
| 단순 선형 회귀분석 (1) | 2020.03.23 |
| 왜 n-1로 나누는가? (0) | 2020.03.17 |