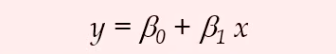
어느 화학자가 온도에 따른 화학물질의 반응속도를 예측하고자 한다.
그러면 온도(x)와 속도(y)를 나타내는 두 변수에 의해 표현되는 함수 관계를 얻을 수 있다.
이때, 화학반응물의 속도와 상품의 판매량에 영향을 미치는 변수를 독립변수(independent variable) 또는 설명변수(explanatory variable)이라고 한다.
그리고 속도와 판매량을 나타내는 변수와 같이 독립변수의 변화에 영향을 받는 변수를 종속변수(dependent variable) 또는 반응변수(response variable)라고 한다.
x : 독립변수, 설명변수, 입력변수
y : 종속변수, 반응변수, 출력변수
독립변수와 종속변수 사이의 관계를 통계적으로 분석하는 방법을 회귀분석(regression analysis)라 한다.
즉 회귀분석은 독립변수가 종속변수에 어떻게 영향을 미치는지 분석하는 방법이다.
이때, 실험에 의해 얻은 온도(x)와 속도(y)의 관측값 (x1,y1), (x2,y2), ... ,(xn,yn) 을 산점도로 나타내면, 이 산점도를 대표할 x와 y사이의 함수 관계를 얻을 수 있다.
y=2x가 나온다면 이와 같은 함수 관계를 회귀방정식(regression equation)이라고 한다.
선형회귀 방정식은 직선만 나타내고 단순 선형회귀방정식은 또 다르다.
단순회귀분석 : x 1개, y 1개
다중회귀분석 : x 여러개, y 1개
하나의 독립변수와 하나의 종속변수 사이의 관계를 추론하는 방법을 단순회귀분석(simple regression analysis)라고 한다.
회귀방정식이 직선인 경우에 이 직선을 회귀직선(regression straight line)이라고 한다.

베타0, 베타1 : unknown constant

^헷을 씌우면 추정량이다.
회귀방정식이 곡선을 나타낼 때 이 곡선을 회귀곡선(regression curve)라 한다.
특히 하나의 독립변수와 하나의 종속변수 사이의 회귀직선을 추론하는 방법을 단순 선형회귀분석(simple linear regression analysis)라고 한다.

x,y 의 관계가 직선인 것만 다룬다.

이게 바로 다중 회귀 분석이다.
이와 같이 두개 이상의 독립변수와 종속변수 사이의 관계를 추론하는 방법을 다중회귀분석(mutiple regression analysis)라고 한다.
그리고 회귀방정식에서 미지의 계수인 베타0, 베타1 등을 회귀계수(coefficient of regression)이라고 한다. 이러한 회귀계수를 결정하고 적합한 회귀곡선을 도출하는 과정을 회귀곡선의 추정이라고 한다.

x는 독립변수, y는 종속변수 이다. 하지만 이 식에서 오차가 생략되어 있다.

엡실론 을 오차항 (random error term) 이라고 한다.
베타0을 절편 (intercept parameter)
베타1을 기울기라고 할 수 있다. (slope parameter)
따라서 다음과 같이 독립인 확률변수들의 관찰값으로 생각할 수 있다.

즉, 우리는 x값이 주어졌을 때 y는 항상 하나의 값으로 나오는게 아니라 분포를 갖게 된다.

Yi 의 기댓값이 바로 β0 + β1 xi 가 될 것이다.
예를 들어, 온도가 x인 화학물질의 반응속도는 β0 + β1 x 로 기대된다.

β1 > 0 이라면 양의 선형 관계에 있다고 한다.
β1 < 0 이라면 음의 선형 관계에 있다고 한다.
오차 분산은 관찰값들로부터 추정될 수 있으며, 이 값이 작을수록 측정값(xi, yi)는 직선에 더욱 가깝게 된다.

우리는 편차가 작길 희망한다.
우리는 편차제곱이 작게하는 직선을 그리고자 한다.
단순회귀모형에 대한 추론을 살펴보면서 다음과 같이 산점도에서 관찰값들을 대표하는 직선을 무수히 많이 그릴 수 있다.

여러가지의 직선으로 그리는것이 다 방법 중 하나이다.
뭐가 제일 좋냐? : 관찰값에 가장 근접한 직선
편차를 구하면 음수가 나올 수 있으므로 편차 제곱 합을 구해서 알 수 있다.
단순회귀모형은 이와 같은 많은 직선들 중에서 가장 적합한 직선을 구하는 것이다.
즉, 관찰값들에 가장 근접하는 직선을 구하는 것이다.
종속변수의 관찰값 yi와 적합 직선의 추정값 베타0 + 베타1 xi 와의 잔차제곱합을 최소로 하는 직선을 선택하는 방법을 많이 사용한다.

한 점만 있을 때는 편차의 제곱을 minimize 하는 방법으로 추정한다.
1. 잔차 제곱 합

따라서 다음과 같은 잔차제곱합을 최소로 하는 β0과 β1을 구하는 것이다.
이와 같이 회귀직선을 구하는 방법을 최소제곱법(least squares method) 라고 한다.
이 방법에 의해 얻은 직선 y^ = β0^ + β1^ x를 추정회귀직선(estimated regression line)이라고 한다.

β0으로, β1로 편미분으로 푼다.

아래 정규방정식의 해는 무조건 암기해야 한다.

Sxx : X 에 대한 제평 평제 = X에 대한 편차 2번
Sxy : X , Y 에 대한 제평 평제 = X에 대한 편차 * Y에 대한 편차



2. 예제 1.


3. 예제 2.



'✏️ Mathemathics > Statistics and Probability' 카테고리의 다른 글
| 최소 제곱법 (0) | 2020.03.25 |
|---|---|
| p-value (0) | 2020.03.23 |
| 왜 n-1로 나누는가? (0) | 2020.03.17 |
| 감마 분포 (Gamma Distribution) (0) | 2020.03.17 |
| 지수분포 (Exponential Distribution) (0) | 2020.03.16 |