


NeRF 논문 리뷰 포스팅입니다. 3D Vision 공부를 시작한 이후 첫 논문 리뷰 및 정리인 만큼 잘못된 부분이 많을 수 있으니, 잘못된 부분은 언제든 코멘트 해주시기 바랍니다.
Introduction
NeRF는 어떤 물체를 찍은 여러장의 사진을 입력 받아, 새로운 view에서 바라본 객체의 모습을 알아내는 view synthesis에 대한 새로운 방식에 대한 논문이다. 즉, N개의 시점에서 찍은 2D image를 받으면, N개의 시점으로 보여주는 것이 아니라 continuous하게 임의의 시점에서 2D image를 만들어내는 것이 이 논문의 핵심이다.

예를 들어, 100개의 시점이 있다면 80개를 input으로 쓰고 Rendering을 거친 다음에 나머지 20개 시점을 만들고, 실제 20개의 시점의 이미지와 비교해서 정량평가를 한다. 여기서 Rendering을 한다는 3D view 정보를 파악하는 과정을 의미하고, NeRF를 학습시키는 과정으로 보면 된다.
정리하자면 NeRF는 3D view를 생성하는 task를 수행하고, 같은 물체를 다양한 시점에서 찍은 이미지가 있을 때, 이 중 일부를 학습에 사용하고 나머지로 평가하는 방식을 주로 사용한다. 즉, 주어진 view를 학습하여 novel view를 생성할 수 있는 모델을 학습한다고 할 수 있다. Novel view synthesis, Image rendering, Scene Representation 3가지를 한 번에 해결한다.
Neural Radiance Field Scene Representation


NeRF는 input으로 3D 위치정보(Spatial location)인 (x, y, z)와 물체를 바라보는 방향(Viewing direction)을 받고, 색상값인 (r, g, b)와 σ(density)를 예측할 수 있는 Fully Connected Neural Network를 학습한다.

input
object 한 점과 카메라의 한 점, 그에 따른 각도 세타가 정해지면, input으로 (x, y, z, 세타, 파이)를 넣는다. 3D 에서는 똑같은 카메라로 보더라도 다른 색깔을 가질 수 있다. 거울이나 물방울에 비치는 대상은 어느방향에 따라서 RGB 값이 다를 수 있다. 실제로는 MLP의 input으로 세타, 파이를 넣는 것이 아닌 Cartesian vector (x', y', z')를 넣는다.
output
output은 그 지점의 (r, g, b, σ) 이고, 여기서 σ는 density이다. density가 가지는 의미는 투명도의 역수 개념이다. density는 그 위치의 RGB 값이 가지는 particle에 대한 density이다. density가 크면 견고해서 뒤에가 안보이는 것이고, density가 낮으면 견고하지 못해서 뒤가 많이 비치는 물체들이다. 즉, density가 낮다 = "투명하다 or 뒤에 있는 것들이 잘 보인다", density가 크다 = "뒤에 있는 것들이 가려진다" 로 해석할 수 있다.
Multi Layer Perceptron
그럼 이 함수를 어떻게 만들건가? MLP로 만든다.
보통 MLP로 학습데이터를 training하고 initialize해서 바로 대상 하나에 대해서 학습하는 과정을 렌더링으로 생각한다. 방대한 양의 train 데이터를 학습하고 test 데이터를 예측을 하는데에 쓰이는게 아니라 그냥 물체 하나가 주어지면 바로 initialize 해서, 모든 위치에 대해서 우리가 원하는 RGB와 density 값이 나오도록 학습한다. 즉, 학습부터가 inference라고 생각하면 된다. Train을 미리 하는게 아니라 Test 시에 input이 들어오면 그 input에 대해서만 학습을 새로 한다.
MLP Structure

총 9개의 FC를 사용하고, ReLU activation function을 사용한다. 여기서 특이한 점은 input으로 처음부터 5차원을 다 넣어주는 것이 아니라 (x, y, z)만 먼저 통과시킨다. 8개의 FC만 통과하게 한 다음 Volume density를 뽑아내고, Viewing direction(d)를 합쳐서 하나의 FC를 통과시킨다. 그리고 나서 RGB 가 나오게끔 한다. 왜냐면 Multi-view consistent 함을 위해서이다.
이렇게 하는 이유는 Non-Lambertian effect(보는 각도에 상관없이 컬러나 반사율이 동일하지 않다) 때문이다. 즉, 보는 각도에 따라 어떤 물체가 밝아졌다 어두워졌다 하기 때문이다.
Volume density는 보는 각도와 상관 없이 동일해야 하기 때문에, Volume density는 오로지 Coordinate 좌표만 가지고 추측할 수 있도록 제한한다. Color는 Viewing direction(d)에 대해서 어떤 함수가 될 수 있도록 d라는 input을 나중에 넣어준다.
결국 8개의 FC layer를 Volume density를 추측하기 위해 사용하고 그 input은 오로지 (x, y, z)이다.
나머지 1개의 FC layer에는 예측된 Volume density와 Viewing direction(d)를 넣어서 RGB값을 추출하게 된다.
그리고 나서 Volume Rendering을 통해 특정한 View point에서 봤을 때의 2D 컬러를 계산할 수 있다.
Volume Randering with Radiance Fields
Ray
NeRF에서 사용하는 개념 중 가장 중요한 개념은 Ray이다.

픽셀값 하나를 만들기 위해서 대상으로부터 카메라 필름까지의 직선을 만들 수 있는데, 직선 위의 모든 particle이 하나의 픽셀의 RGB를 만드는데에 영향을 미친다. 원점 카메라 초점 위치(o)로부터 어떤 방향(d)으로 t만큼 이동한 점들의 집합으로 Ray라는 직선을 정의하게 된다.
그럼 Ray의 Projection에 대해서 어떻게 정의할까?
어떤 시점에서 본래의 이미지를 얻고 싶으면 모든 픽셀에 대해서 Ray를 정의해야 한다. 카메라 위치와 픽셀 위치가 정해지면, 두 지점을 잇는 직선이 정의가 될 것이고, 직선 위의 모든 물체나 물질이 다 모여서 이 직선의 RGB값을 결정하게 된다. 이런 모델을 가지고 렌더링을 하게 된다.
이렇게 카메라 초점 위치(o)와 viewing direction(d)이 정해지면 Ray 위에 있는 3d point들의 좌표는 t값에 대해 o+td를 통해 계산할 수 있다.

이렇게 정해진 픽셀 값은 한 Ray 위에 존재하는 point들의 RGB 값(Neural Radiance Field에서 정의한 함수의 output 인 c값)들의 Weighted Sum이 된다.
그럼 Weighted Sum은 어떻게 정의할까?
Classical Volume Rendering (= Ray marching)

Classical Volume Rendering은 3차원의 영역을 특정한 view point에서 바라봤을 때, 2D 이미지로 렌더링 하고 어떤 컬러를 갖는지 계산하는 방법이다. Volume 정보를 가지고 있는 물체로부터 이미지 컬러를 랜더링한다. 화살표 방향은 랜더링 하는 방향이고, 화살표 반대 방향이 우리가 쳐다보는 방향이다.
Ray 상에 있는 점들이 가지는 color 값들을 weighted sum하면, 카메라 위치(o)에서 바라봤을 때 보이는 2D 이미지 상의 하나의 픽셀이 가지는 color 값을 구할 수 있다.
직관적으로 보면 아래와 같이 순서를 정리할 수 있다.

- Ray casting : view 방향과 일치하는 방향으로 모든 픽셀에서 Ray를 쏘고
- Sampling : 선상의 모든 점을 더하는 것은 불가능하므로 적절한 간격을 가지고 최종 색상을 결정할 데이터를 선택하고
- Shading : 그 포인트에 대한 3D 컬러와 Volume density를 얻고
- Compositing : 결정된 Ray 위의 모든 샘플링 데이터를 더해주면 2D 컬러가 나온다.
즉, NeRF에서 쓰이는 방법은 Ray marching 방법이다.
Ray casting으로 광선이 3D 물체와 처음으로 교차하는 지점을 찾고, Ray marching을 통해 광선이 지나가는 경로 전체를 고려하여 볼륨 내부와 상호작용하는 방식으로 렌더링한다. Ray tracing과 헷갈릴 수 있는데, Ray tracing은 광선이 물체와 교차하는 지점을 찾고, 그 지점에서의 색상과 조명을 계산하는 기법이다. 반면, Ray marching은 광선을 따라가며 여러 지점에서 샘플링을 수행하고, 이를 통해 볼륨 내부의 밀도와 색상을 통합하는 방식으로 작동한다.
Weighted Sum
아래 두가지 방식을 기준으로 Weighted Sum을 정의한다.
- Density가 클수록 Weight가 커야한다. 그 지점이 유리나 흐물흐물한 것이면 Weight가 작아야하고, 견고한 것이면 Weight가 커야한다.
- 그 지점을 가로막고 있는 점들의 Density의 합이 작을수록 그 지점의 Weight가 커야 한다. 즉, 어떤 물체를 보려면 그 물체 앞에 있는 particle들의 Density가 작아야 그 물체를 볼 수 있다.
위의 두가지를 반영한 식이 아래의 식이다.

- r : 하나의 Ray
- C^(r) : 어떤 Ray에 대해서 픽셀로 Projection 돼서 정해진 RGB 값
- tn, tf : 어떤 Ray가 물체를 통과할 때의 시작점(tn)과 끝점(tf)
- t : weighted sum을 할 위치까지
- T(t) : t보다 앞에 있는 점들의 density 합(2. 방식을 반영한 것), 보고싶은 물체의 앞에있는 particle들의 density를 적분, 이 값이 크면 보려는 물체가 물체 앞의 particle에 가려져 보이지 않기 때문에 -부호가 붙는다.
- o(r(t)) : t지점의 density (1. 방식을 반영한 것), density가 클수록 t지점에서의 색상이 투명하지 않고 진하다는 것을 의미하여 색상에 가중치를 크게 주는 것으로 해석할 수 있다.
- c(r(t), d) : t 지점의 RGB 값, 실제 RGB값의 weighted sum

- T(1 - exp()) = Contribution weight = 어떤 색이 2D 이미지의 색깔에 얼마만큼 contribution 할 수 있는가
- T = 3D point 앞에 얼마만큼 물체가 가로막고 있는가
- 1 - exp() = Volume을 얼마나 3D point에서 차지하고 있는가
이 식을 바탕으로 2D 컬러는 3차원 컬러의 weighted sum이라고 이해할 수 있다.
즉, 우리가 대상으로 하는 t라는 점까지에서, density가 큰 애들이라면 그 값이 작아질 것이고, 그 지점까지 density가 다 고만고만하고 낮다면, 그 값이 커질 것이다. 이렇게 두가지의 weight를 반영한다.
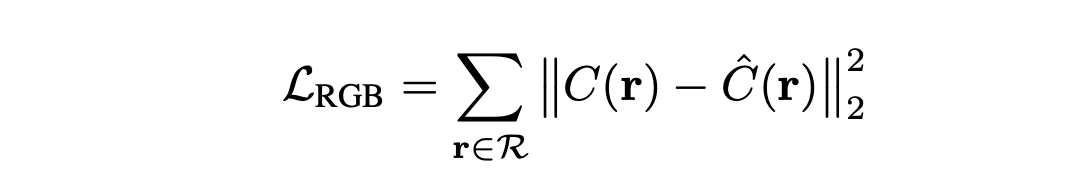
c(r(t), d) 와 density인 o(r(t))를 F라는 Neural Network를 통해 얻고, 이렇게 얻은 값을 통해서 C^(r) 을 만들어내고, 이것에 대한 GT인 C(r) 과의 L2 loss를 minimize 하게 되면, F가 학습이 잘 되겠구나 라고 생각하면 된다.
지금까지 내용을 요약하자면, Ray로부터 얻은 픽셀값은 RGB값이 될텐데, 이 RGB값은 카메라로부터 얻는 값이기 때문에 직선 상에 있는 모든 particle들의 RGB 값의 weighted sum이 된다. 그 과정에서 weight는 어떤 점이 커야되냐 는 내용이다.
Stratified sampling approach
Ray가 접촉하는 모든 점에서 샘플링한 점(ti)들을 가지고 적분을 수행하기 때문에 불필요한 pixel도 적분 범위에 들어가 성능이 제한되어 버리는 것을 방지해야 한다. 그렇기 때문에 이용하는 방법이 Stratified sampling approach 이다.
먼저 식에서는 t라는 점까지의 적분을 하고 있고, 무한한 t에 대해서 적분하는 것이 불가능하기 때문에 t를 샘플링 해주어야 한다. 아래 그림과 같이 Ray를 n등분을 해서 각 segment 안에서, uniform distribution으로 랜덤하게 segment를 뽑는다. 그러면 t1 ~ tn 까지 뽑히게 된다.
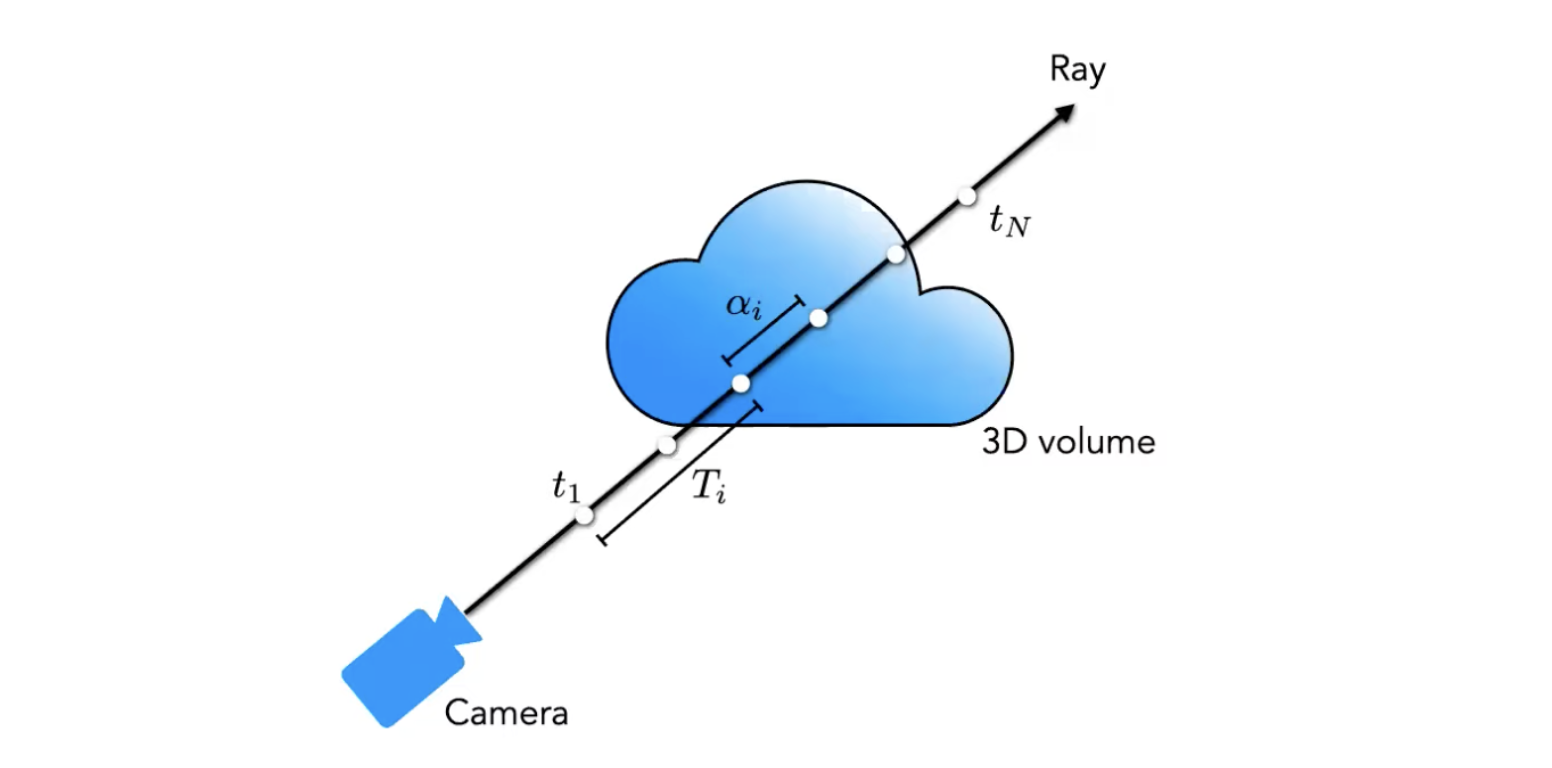

이렇게 적분에 쓸 값을 선별하면 'continuous position을 처리하는 MLP에서 얻은 값을 선별하기 때문'에 유효한 값들에서 sampling을 수행할 수 있다. 그렇게 sampling한 ti들을 가지고 적분을 수행하면 더 높은 성능이 나온다.
이 때 수행하는 적분은 quadrature rule을 따르는 discrete한 적분이다. 아래 식을 보면 Ray에 대한 식인 C(r)이 변해있는데, 이 식은 "Optical models for direct volume rendering" 논문을 참고해서 Ray를 따라서 적분하는 것을 discrete하게 바꾼 식이다. 이렇게 적용하면 n이 커질수록 continuous한 버전에 수렴을 한다는 내용이다. 결과적으로 구현할 땐 아래의 식으로 구현을 해야한다.
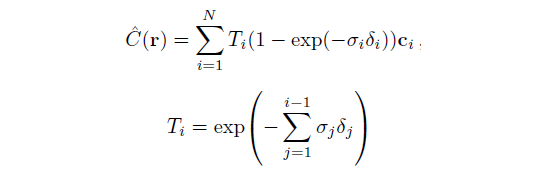
Optimizing a Neural Radiance Field
NeRF가 high-resolution complex scene을 표현할 수 있게 사용한 방법 2가지가 있다. 바로 Positional encoding과 Hierarchical sampling 이다. 이 둘을 이용하여 high frequency를 잘 표현한다.
Positional encoding
Positional encoding은 input으로 넣어주는 5D low dimension한 것을, high frequency function을 통해 조금 더 high dimension한 space로 맵핑을 한 다음, Neural Network를 통과시키면 실제 이미지나 데이터가 가지고 있는 high frequency 를 잘 표현할 수 있다는 것이다.
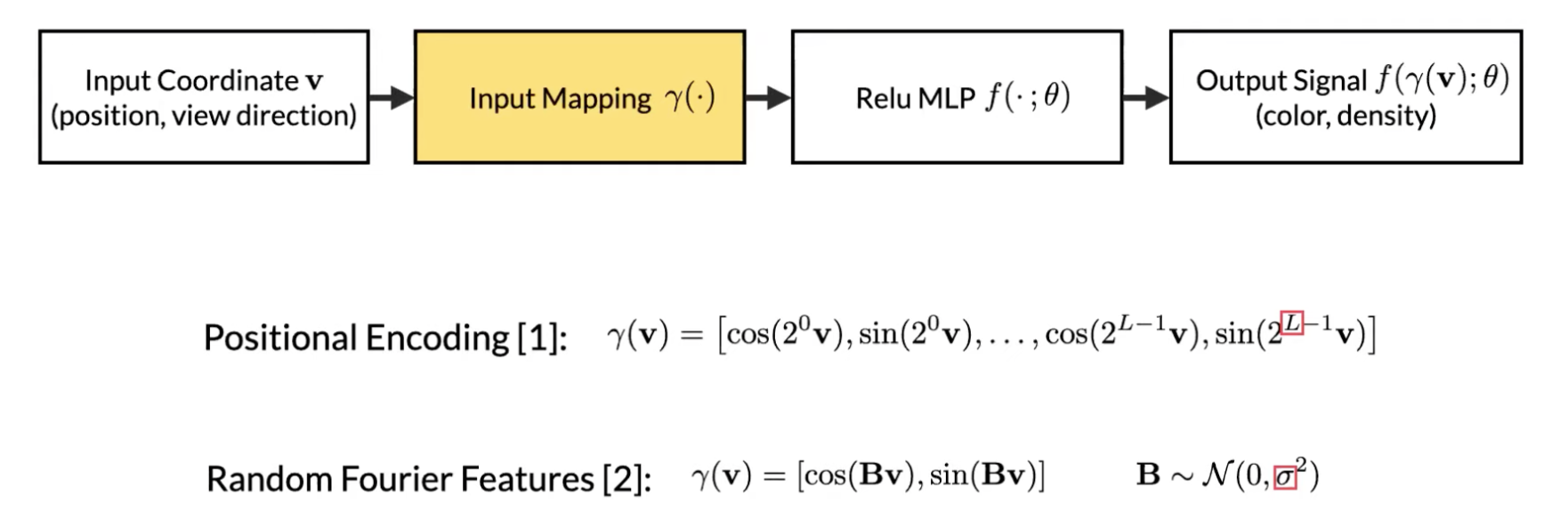
sin, cos을 갖는 function에 5D input v를 맵핑 한 다음, Neural Network에 통과시키면 조금더 high frequency 정보를 잘 표현한다고 한다. 여기서 L은 차원 수이며, 3D position에 대해서는 10개를 사용하고, Viewing direction에 대해서는 4개를 사용했다. 둘을 다르게 준 이유는 나오지는 않았지만 Geometry에 의한 high frequency component가 Color에 의한 high frequency component보다 많기 때문이라고 추측된다.
MLP structure에서 input에 5D인 5가 아니라 60, 60, 24 이렇게 적혀있는데, 이렇게 넣어주는 이유가 바로 Positional encoding을 통한 차원을 늘려서 input을 준 것이다. 여기서 60은 (x, y, z) 인 3개 x 20 으로 증강해서 맵핑한 다음 넣어준 것이고, 24개를 넣어주는 Viewing direction은, 사실상 세타 파이를 넣어주지 않고, Cartesian vector(직각 좌표)를 사용해서 (x', y', z')으로 넣어준다. 3개의 파라미터를 넣어주는 것이다.

이렇게 Positional Encoding을 한 후 input으로 넣어주는 것이 아래 그림처럼 훨씬 더 좋은 학습이 된다고 한다.

Hierarchical volume sampling
좋은 샘플들을 얻기 위한 또 하나의 방법으로 Hierarchical volume sampling을 이용한다. 샘플링 할 때에 공기가 있는 부분보다 실제로 물체가 있는 부분을 샘플링 하는 것이 유리하다. 즉, 집중하고 싶은 부분을 최대한 많이 샘플링하는 방법이다. 이 방법은 2 step으로 이루어진다. (Coarse Network, Fine Network)
Coarse Network

Course 과정에서 Nc개의 구역으로 나누고, 각각의 구역에서 point를 하나씩 뽑는다. 얘내들을 먼저 FCN의 input으로 넣어준다. 그럼 output으로 Nc개에 대한 density(σ)와 color(ci)가 나온다. 그리고 Contribution weight(wi)를 계산하고 nomalize 해준다. 왜냐면 normalize를 해야 Nc개의 point들이 각각 최종적인 컬러에 얼마만큼의 확률로 기여하는지, 반영하는지를 알 수 있다. (Coarse : 정확한 2D projection, but 부정확할 수도 있는 3D position)
Fine Network
여기서 조금 더 Color contribution에 기여하는 point들을 더 샘플링 하고 싶다. 그러려면 위에서의 probablity distribution을 고려한 샘플링 방법이 도입이 되어야 한다. 그래서 도입되는 것이 Inverse transform sampling 이다. 이 방법은 모든 확률 분포의 누적 분포 함수(cumulative distirbution function, cdf)가 균등분포(Uniform distribution)를 따른다는 성질을 이용한 방법이다.
Inverse transform sampling를 통해서 총 Nf개의 샘플을 뽑아낸다.

이렇게 뽑아낸 Nc개와 Nf개의 샘플들을 새로운 MLP인 Fine Network에 통과를 시켜준다. 그리고 output으로 똑같이 σ와 c 값을 얻어낸다.

요약하자면
- Network를 2개 쓰는데,
- Course Network에서는 Rough 하게 Nc개의 포인트를 뽑아 Color contribution을 계산하고(probability distribution을 얻는 과정),
- Fine Network에서는 앞에서 얻어낸 것들을 가지고 조금더 Color contribution에 기여하는 포인트 Nf개를 뽑아서, Nc + Nf 개의 포인트를 사용해서 실제의 Volume density와 color를 얻어낸다.
이렇게 관심있는 영역(Nc + Nf)들에 대해서만 뽑았기 때문에 계산이 좀더 간단해지고 Back propagation 할 때에도 gradient가 잘 계산이 된다. 이렇게 2 step으로 이루어지기 때문에 Hierarchical volume sampling이라고 불린다. 이렇게 Color를 Render 할 수 있다.
Implementation details
이 Network을 Training할 때, 어떻게 Loss를 줄까?
단순하게 아래의 식과 같이 예측했던 Color와 실제 Color를 비교한다.

실험에선 input으로 4096개의 Ray를 주는데, 하나의 Ray당 Nc + Nf 개를 갖고 이는 실험에서 256개를 이용했기 때문에 총 4096x256개의 3D 포인트를 사용해서 학습시키고, 실제 색깔인 C(r)과 Course Network가 추측한 색깔인 C^c(r), Fine Network가 추측한 C^f(r)의 차이를 계산해서 Loss로 사용한다.
여기서 Course Network Loss까지 사용하는 이유는 Course Network가 판단한 것 기반으로 한 번 더 샘플링을 하기 때문이다.
이렇게 두가지 Rendering Loss를 넣어서 학습시킨다.

Training NeRF
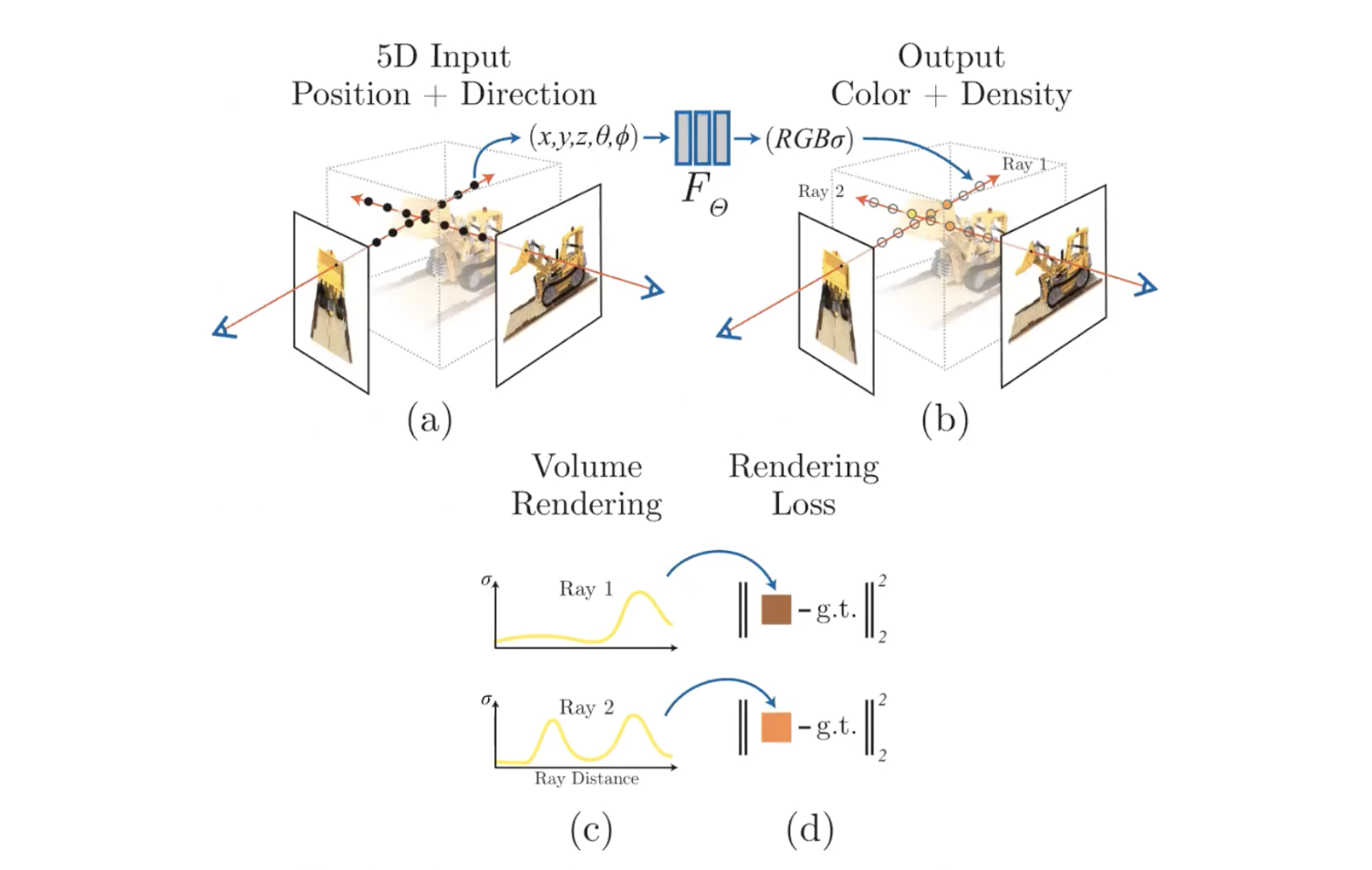
- View point selection
- Ray composition
- Select 5D input samples along the ray
- Query into MLP
- Get predicted color + density
- Render color using colume ray casting
- Compute rendering loss(Simply squared error between rendered and true pixel colors)
자세한 Training 과정은 아래 포스팅 참조
NeRF Training
NeRF Training 각각의 Ray 상의 Radiance로부터 weighted sum된 RGB와 density 값을 가지고 Volume Rendering을 거쳐서 얻은 각각의 pixel 값을 구해야 한다. 그리고 그 pixel값과 Ground Truth의 RGB와의 MSE L..
woochan-autobiography.tistory.com
Reference
NeRF 논문 : https://www.ecva.net/papers/eccv_2020/papers_ECCV/papers/123460392.pdf
Arxiv : https://arxiv.org/abs/2003.08934
NeRF website : https://www.matthewtancik.com/nerf
NeRF github : https://github.com/bmild/nerf
Jon Barron - Understanding and Extending Neural Radiance Fields
Review : Postech Seminar, PR-302
Volume Randering : https://lobotomi.tistory.com/35
.
'🖼 Computer Vision > Paper Review' 카테고리의 다른 글
| Paper Review - Plenoxels (Radiance Fields without Neural Network) (1) | 2022.08.30 |
|---|---|
| Paper Review - PlenOctrees (0) | 2022.08.27 |
| Paper Review - NSVF (Neural Sparse Voxel Fields) (0) | 2022.08.26 |
| 논문 읽기와 ML/DL 커리어 경력에 대한 조언 by 앤드류 응 (0) | 2022.06.16 |