
📌 이 글은 권철민님의 딥러닝 CNN 완벽 가이드를 바탕으로 정리한 내용입니다.
목차
- Cross Entropy를 통한 Loss
- Cross Entropy 와 Squared Error 비교
- Cross Entropy - Sigmoid의 경우 계산하는 방법
- Cross Entropy 정리
Cross Entropy를 통한 Loss

예측 정확도를 늘려보자.

0.3 → 0.4
0.5 → 0.7
0.5 → 0.8
Loss를 감소시키려면 Gradient Descent가 잘 설정이 되어있어야 하고,
여기에 기반해서 Confidence를 높이는 방향으로 해서,
Loss를 낮출 수 있다.
Cross Entropy와 Squared Error 비교

Squared Error 기반은 일반적으로 잘못된 예측에 대해서 상대적으로 CE보다 높은 비율의 페널티가 부여되어,
Loss 값의 변화가 상대적으로 심하다.
그렇기 때문에 Cross Entropy에 비해 최적 수렴이 어렵다. 최적화가 힘들다.
Squared Error가 0.01 에서 0.09 까지 늘어나는데 9배나 증가한다.
반면에 Cross Entropy는 0.105 → 0.356 → 0.693 이렇게 3배씩 증가한다.
이런 변화율이 Squared Error에서는 심하기 때문에 Cross Entropy에 비해서는 최적 수렴이 어렵다.
Cross Entropy - Sigmoid 일 경우 계산하는 방법

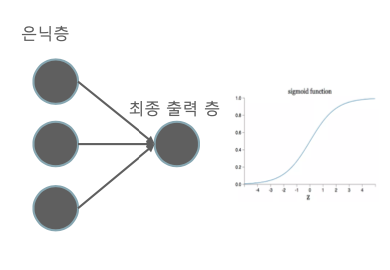
이진 분류 때,
보통 최종 출력층에서 0 또는 1이 출력되고, 그걸 시그모이드 함수에 적용하면
Cross Entropy는 아래와 같이 계산된다.

여기서 yi^ 은 시그모이드가 적용된 값이다.
그런데 뒤에 (1-yi)*log(1-yi^) 은 왜 있는걸까?
실제값이 1이면 (1-yi)*log(1-yi^) 은 0이 된다.
반대로 실제값이 0이면 yi*log(yi^) 이 0이 된다.

Cross Entropy Loss 정리

이렇게 딥러닝 네트워크가 구성이 되어있을 때,
맨 마지막에 Classification 출력층은 Softmax가 될 수도 있고, Sigmoid가 될 수도 있다.

그래서 Cross Entropy Loss를 계산하는 방법은,
Multi Class일 경우, Softmax Cross Entropy Loss 또는 Categorical Cross Entropy Loss 라고 하고,
Binary Class일 경우, Binary Cross Entropy Loss 라고도 하고, Sigmoid Cross Entropy Loss, 또는 Log Loss 라고도 한다.
'🖼 Computer Vision > CNN' 카테고리의 다른 글
| CNN - Training Epoch, Batch Size, Learning Rate (0) | 2022.01.20 |
|---|---|
| CNN - Optimizer (0) | 2022.01.20 |
| CNN - Loss function (0) | 2022.01.20 |
| CNN - Activation function (활성화 함수) (0) | 2022.01.20 |
| CNN - Backpropagation의 Gradient 적용 메커니즘 (0) | 2022.01.19 |