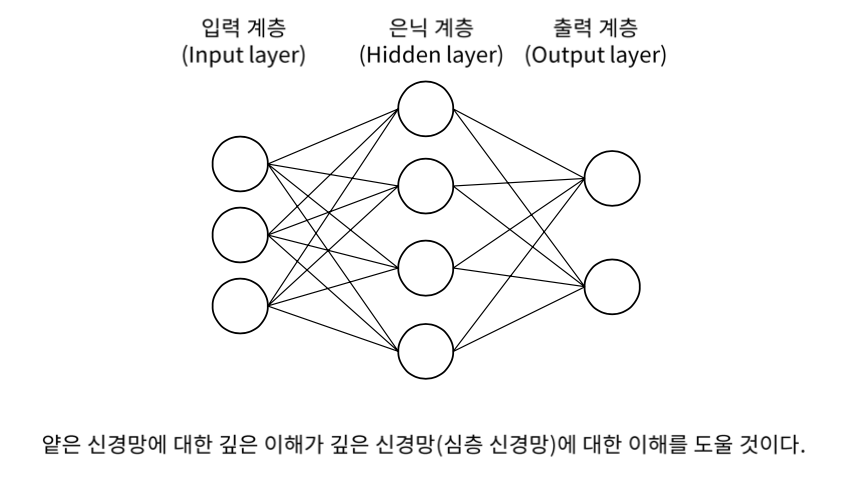

얕은 신경망은 입력, 은닉, 출력 계층으로 이루어져 있다.
뉴런의 수학적 표현

뉴런은 입력이 들어오면 각 입력의 가중치가 곱해지고, 그것을 전부 더해줘서 마지막에 활성함수를 통해 출력을 낸다.
출력이 y라면 입력 xi에 가중치 wi를 곱해서 Bias를 더한 후 활성함수 a() 를 통과한다.
입력치와 가중치를 곱한 것은 두 벡터의 내적과 같다.
Bias가 없을 경우 뉴런이 표현할 수 있는 그래프는 원점을 지나는 선밖에 없다.
따라서 Bias는 항상 있는 것으로 생각해 주어도 된다.
가중치(weight)란?
뉴런의 연결선 색이 다르다는 것은 입력 데이터가 각기 다른 값으로 뉴런으로 전달되었다는 의미이다. 데이터의 값은 같은데 다른 값으로 전달되려면 이 입력값에 각기 다르게 곱해지는 수치가 있어야할 것이다. 이것이 바로 가중치(weight)이다. 전혀 어려울 것이 없다. 가중치라는 원 단어의 뜻을 생각해봐도, 데이터를 각기 다른 비중으로 h1, h2로 전달시키기 위해 웨이트(weight), 즉 비중(=가중치)을 다르게 한다고 받아들이면 이해하기가 쉬울 것이다.
편향(bias)이란?
편향(bias)은 하나의 뉴런으로 입력된 모든 값을 다 더한 다음에(가중합이라고 한다) 이 값에 더 해주는 상수이다. 이 값은 하나의 뉴런에서 활성화 함수를 거쳐 최종적으로 출력되는 값을 조절하는 역할을 한다. 순서상 편향이 먼저 나왔지만 다음에 설명할 활성화 함수를 알게 되면 이 값의 역할도 쉽게 이해된다.
활성화 함수(Activation function)란?
우리가 사는 세상을 한번 생각해 보자. 실제 세계에서는 입력값에 비례해서 출력값이 나오지가 않을 때도 많다. 대개는 어떤 임계점이 있고 그 임계점을 경계로 큰 변화가 생긴다. 물이 끓는 것도 그렇고 비행기가 이륙하는 것도 그렇다.
마찬가지로 뇌의 뉴런도 하나의 뉴런에서 다른 뉴런으로 신호를 전달할 때 어떤 임계점을 경계로 출력값에 큰 변화가 있는 것으로 추정된다.
인공 신경망은 디지털 세계이긴 하지만 뇌의 구조를 모방하므로 임계점을 설정하고 출력값에 변화를 주는 함수를 이용한다. 이 활성화 함수 덕분에 은닉층으로 인한 좌표평면 왜곡효과도 발생합니다. 앞에서 설명한 편향은 임계점을 얼마나 쉽게 넘을지 말지를 조절해주는 값이라고 생각하면 된다.
활성화 함수에는 시그모이드(Sigmoid) 함수, 렐루(ReLU) 함수, 항등 함수, 소프트맥스 등 여러 종류가 있다.
전결합 계층의 수학적 표현

입력 계층(Input Layer)

머신 러닝은 특징 추출을 직접 해주어야 한다.
무엇을 입력으로 주어야 하는가? -> 어떤 입력을 사용해야 출력과 연관이 있을 것이냐에 대한 문제이다.
굵은 x 는 벡터를 말하고 얇은 x는 스칼라, 즉 숫자를 의미한다.
세로형태의 긴 형태이지만 보기 쉽게 가로로 쓴 후 Transpose 해준다.
수학적으로 많이 쓰는 표현이니 익숙해져야 한다.
은닉 계층(Hidden Layer)

입출력에는 드러나지 않기 때문에 Hidden Layer라고 부른다.
가장 핵심적인 계층이다.
출력 계층(Out Layer)

이제 한번 종합해 보자. 층이 많은 인공 신경망은(딥러닝)은 데이터를 입력받아 그 데이터들에 각기 다른 가중치를 곱해 다음 층의 뉴런으로 전달하는 과정을 반복적으로 거치면서 마지막에 최종적인 출력값을 계산한다. 그렇다면 이 과정에서 구체적으로 계산해야 되는 수치들은 무엇일까?

이 신경망에서 원(뉴런) 안에 있는 값은 이미 알고 있거나(입력 데이터1, 2), 가중치와 편향, 활성화 함수만 알면 구할 수 있는 값들이다.
문제는 파란색으로 나타낸 가중치(w1, w2, …..)와 편향(b1, b2,…..) 값이다.
이 값들은 기존 데이터를 학습해서 가장 적절한 값들을 찾아내야 하는 수치로서, 성능이 좋은 딥러닝을 구축한다는 것은 결국 이 수치들의 최적값을 구해야 하는 것이다.
그럼 가중치와 편향을 구하는 원리와 과정은 어떻게 이뤄지는지 알아보자.
역전파를 통해 최적의 가중치와 편향 구하기
드디어 역전파라는 단어가 등장했다. 일단 잠시 잊어도 좋으니 신경을 꺼두자.
처음에는 최적의 가중치와 편향을 모르니까 일단은 임의로 설정한다. 밑의 그림을 보면, 입력 데이터를 받아 임의로 설정된 가중치를 곱하고 편향을 더해 뉴런에서 뉴런으로 전달한 뒤 최종적으로 출력값 1을 얻었고, 그런데 실젯값(정답)이 7이라고 가정하자. 그럼 6만큼의 차이(오류)가 생겼다.

이 결과를 보면 처음에 임의로 설정한 가중치들과 편향은 적절한 값이 아니라는 것이 분명해졌다. 그렇다면 이제 가중치와 편향을 다른 값으로 바꿔야 한다.

위의 그림처럼 아예 다른 가중치와 편향을 임의로 설정하는 방법이 있지만, 뉴런의 수가 많은 경우에는 가중치와 편향의 가능한 조합이 무한대라 사실상 이 방법은 불가능하다. 그래서 사용하는 방법은 아래 그림처럼 처음 설정한 신경망 구조를 조금씩, 계속 개선하는 방법이다. 여기서는 색으로 구분해서 표현해보겠다.

차이점이 보이는가? 초기에 설정한 신경망 구조를 아주 조금만 변화시켰다. 오른편의 바뀐 신경망에서 연결선과 뉴런의 색이 처음(왼쪽)보다 아주 조금 바뀌었다. 구조를 조금 바꾼다는 것은 각 가중치와 편향 값을 처음 설정한 값에서 아주 조금만 변화시킨다는 의미이다.

위의 그림은 최종 은닉층과 출력층만 떼어낸 그림이다. 이제 출력값과 실젯값의 차이는 6이다.
이 차이 6을 만들어내는데 w5, w6, b3이 일정부분 역할을 했을 것이다. 그래서 차이(오류)를 줄이는 방향으로 w5, w6, b3도 조금 바꾸자는 것이다.
그림에서는 그냥 차이(오류)가 6이다고 설명했지만, 실제로는 (출력값 – 실젯값)2 의 수식으로 표현한다(이를 손실 함수라고 한다). 이 식은 당연히 값을 만드는 데 기여하는 w5, w6, b3을 포함한다.
이때 아주 작은 w5의 변화량에 따른 (출력값 – 실젯값)2의 변화량을 구할 수 있다. 이를 다른 말로 표현하면 (출력값 – 차이값)2를 w5로 미분한다고 한다. 처음 설정한 w5 값은 차이(오류)를 줄이는 방향으로 다음과 같이 조금 수정할 수 있다.

새로운 w5를 구한 것처럼 신경망을 구성하는 모든 가중치와 편향을 위의 방식(출력값과 실젯값의 차이를 조금 줄이는 방식)으로 오른쪽(출력층)에서 왼쪽(입력층) 방향으로 역방향으로 하나씩 수정한다.
아래 그림은 이 과정을 표현한 것이다.

이런 방식으로 새로운 가중치와 편향을 구하면 처음 설정한 신경망 구조를 아주 조금 개선한 새로운 신경망을 구축할 수 있다.
그럼 이 다음에는 어떻게 하는건가?
조금 개선한 신경망으로 새로운 출력값을 구하고 다시 실젯값과의 차이를 구한 다음 이 차이를 또 줄이도록 모든 가중치와 편향을 조금 수정한다. 이 과정을 계속 반복하다보면 어느 시점에 이르러 최적화된 가중치와 편향 값을 구할 수 있다.
이것이 바로 역전파(backpropagation), 즉 오차의 역전파라고 부르는 방법이며 딥러닝의 실체이자 핵심이다.
reference : www.popit.kr
'💡 AI > DL' 카테고리의 다른 글
| SNN을 이용한 Classification, Sigmoid function (0) | 2021.01.27 |
|---|---|
| 회귀 문제의 이해 (0) | 2021.01.27 |
| Shallow Neural Network를 이용한 분류와 회귀 (0) | 2021.01.27 |
| Shallow Neural Network의 구조 (0) | 2021.01.27 |
| 딥러닝의 역사 (0) | 2021.01.27 |