
풀어야할 인스턴스를 몇개로 나눈다.
부분으로 나누고 그 각 부분을 재귀적으로 해를 구한다.
그리고 원래 instance의 해를 구하는 것이다.

Binary Search가 가장 기본적인 Divide and conquer이다.

>> 합병정렬 알고리즘의 구체적인 개념
합병 정렬(merge sort) 알고리즘의 구체적인 개념
하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
합병 정렬은 다음의 단계들로 이루어진다.
•분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
•정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
•결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
합병 정렬의 과정
•추가적인 리스트가 필요하다.
•각 부분 배열을 정렬할 때도 합병 정렬을 순환적으로 호출하여 적용한다.
•합병 정렬에서 실제로 정렬이 이루어지는 시점은 2개의 리스트를 합병(merge)하는 단계 이다.

배열에 27, 10, 12, 20, 25, 13, 15, 22이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.
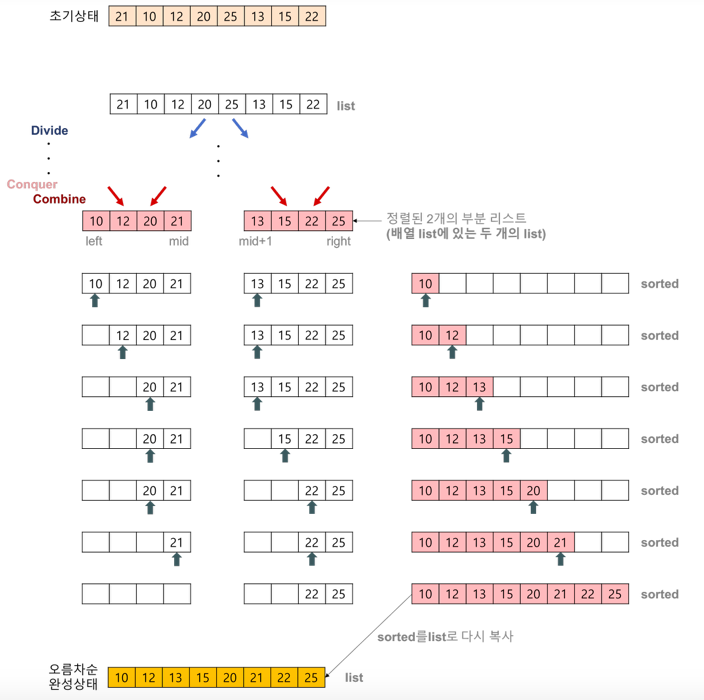
2개의 정렬된 리스트를 합병(merge)하는 과정
•2개의 리스트의 값들을 처음부터 하나씩 비교하여 두 개의 리스트의 값 중에서 더 작은 값을 새로운 리스트(sorted)로 옮긴다.
•둘 중에서 하나가 끝날 때까지 이 과정을 되풀이한다.
•만약 둘 중에서 하나의 리스트가 먼저 끝나게 되면 나머지 리스트의 값들을 전부 새로운 리스트(sorted)로 복사한다.
•새로운 리스트(sorted)를 원래의 리스트(list)로 옮긴다.
병 정렬(merge sort) 알고리즘의 특징
단점
•만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요하다.
•제자리 정렬(in-place sorting)이 아니다.
•레크드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래한다.
장점
•안정적인 정렬 방법
•데이터의 분포에 영향을 덜 받는다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하다. (O(nlog₂n)로 동일)
•만약 레코드를 연결 리스트(Linked List)로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다.
•제자리 정렬(in-place sorting)로 구현할 수 있다.
•따라서 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 다른 어떤 졍렬 방법보다 효율적이다.
합병 정렬(merge sort)의 시간복잡도
시간복잡도를 계산한다면
- 분할 단계
비교 연산과 이동 연산이 수행되지 않는다.
- 합병 단계
비교 횟수

순환 호출의 깊이 (합병 단계의 수)
- 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n)임을 알 수 있다.
- k=log₂n
각 합병 단계의 비교 연산
- 크기 1인 부분 배열 2개를 합병하는 데는 최대 2번의 비교 연산이 필요하고, 부분 배열의 쌍이 4개이므로 24=8번의 비교 연산이 필요하다. 다음 단계에서는 크기 2인 부분 배열 2개를 합병하는 데 최대 4번의 비교 연산이 필요하고, 부분 배열의 쌍이 2개이므로 42=8번의 비교 연산이 필요하다. 마지막 단계에서는 크기 4인 부분 배열 2개를 합병하는 데는 최대 8번의 비교 연산이 필요하고, 부분 배열의 쌍이 1개이므로 8*1=8번의 비교 연산이 필요하다. 이것을 일반화하면 하나의 합병 단계에서는 최대 n번의 비교 연산을 수행함을 알 수 있다.
- 최대 n번
- 순환 호출의 깊이 만큼의 합병 단계 * 각 합병 단계의 비교 연산 = nlog₂n
이동 횟수
- 순환 호출의 깊이 (합병 단계의 수)
k=log₂n - 각 합병 단계의 이동 연산
임시 배열에 복사했다가 다시 가져와야 되므로 이동 연산은 총 부분 배열에 들어 있는 요소의 개수가 n인 경우, 레코드의 이동이 2n번 발생한다. - 순환 호출의 깊이 만큼의 합병 단계 * 각 합병 단계의 이동 연산 = 2nlog₂n
T(n) = nlog₂n(비교) + 2nlog₂n(이동) = 3nlog₂n = O(nlog₂n)
https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
[알고리즘] 합병 정렬(merge sort)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
merge sort는 interation이랑 recursive 버젼 두개를 배웠을 것이다.
n개의 원소를 sorting 한다.
왼쪽 n/2개, 오른쪽 n/2개 재귀적으로 merge sort 한다.
왼쪽과 오른쪽을 결합해서 전체로서 sorting되게 한다.
여기 슬라이드에 있듯이 merge sort를 세 부분으로 나누면
1. Divide
2. Conquer
3. Combine
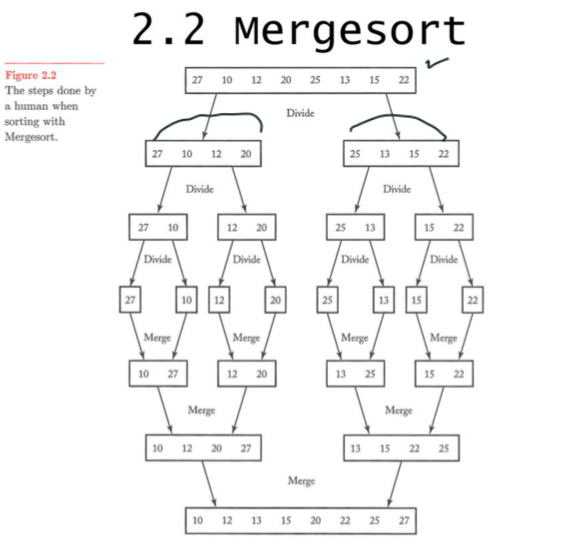
8개 원소를 merge sort
-> 4개 원소를 merge sort
-> 2개 원소를 merge sort
-> 1개 원소를 merge sort
-> 1개를 반개로 나눌 수 없으므로 아무것도 하지 않는다.

U도 V도 아닌 제 3의 배열 S에 10을 쓴다.
U의 inex를 1 증가시킨다.
그 후 비교한다.
12를 갖다 쓴다.
U도 V도 아닌 제 3의 배열 S에 12를 쓴다.
U의 index를 1 증가시킨다.
그 후 비교한다.
13을 갖다 쓴다.
U도 V도 아닌 제 3의 배열 S에 13을 쓴다.
.
.
.

u의 원소 갯수 : h
v의 원소 갯수 : m
h와 m의 값이 달라도 상관 없다.
u의 원소의 개수와 v의 원소의 갯수의 합에 비례하게 끔 시간이 걸린다.
O(h+m-1) 이다.
비교는 n-1 번
copy는 n 번

n>1 일 때만 한다. ★★★★★★★
원소가 두 개 이상일 때만 한다.
알고리즘이 끝나야 하기 때문에.
시간 복잡도를 구해보자
T(n)

이것의 시간은 T(n/2)이다.
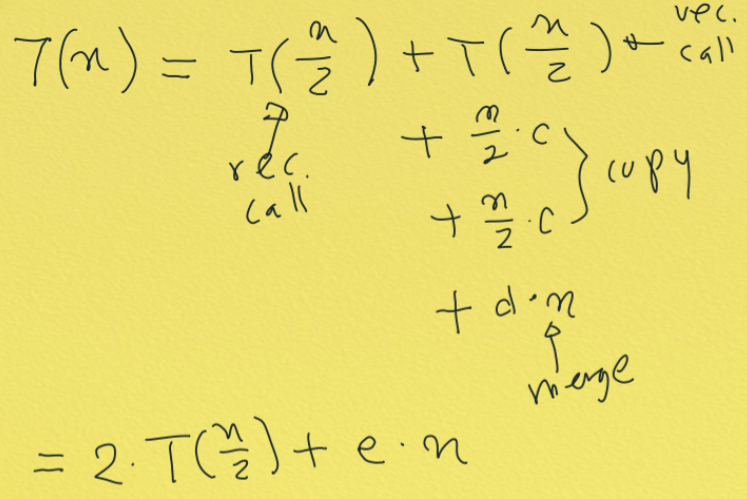

다시 씀

이게 merge sort 함수의 시간 복잡도 이다.
1/2로 나눈 다음에
재귀적으로 콜한 다음에
계속해서 merge 가 일어난다.
이게 끝이다
8 -> 4 -> 2 -> 1 -> 2 -> 4 -> 8

단점 : copy를 하기 때문에 시간이 많이 걸린다
또한 메모리도 많이 차지한다.
입력된 배열 안에서 자리를 바꾸는게 아니라 다른 배열에 가서 copy를 해서 가져와야 하므로
대부분의 정렬 알고리즘이 in-place 지만 merge sort는 그게 아니다.
배열 안에서 하는 것 : in-place

메모리가 좀 덜 쓰는 merg sort 2
'🕶 Algorithm > 알고리즘' 카테고리의 다른 글
| Divide-and-Conquer (part2) (0) | 2020.03.31 |
|---|---|
| 알고리즘 과제 #1 (0) | 2020.03.28 |
| Algorithms Chapter 1 (part4) (0) | 2020.03.23 |
| Algorithms Chapter 1 (part3) (0) | 2020.03.19 |
| Algorithms Chapter 1 (part2) (0) | 2020.03.16 |