

Order는 한마디로 하면 시간복잡도 함수에서 상수를 무시하고
n값(input)이 클 때 어떻게 behave하느냐를 나타낸다.
우리가 다루는 알고리즘의 효율성이라는 것은 input사이즈가 클 때 문제가 된다.
왜 무시하느냐?
3n^2인 것은 다른 컴퓨터로 돌리면 0.5n^2 정도 차이밖에 안난다.
그래서 상수를 무시하고 나타낸다.
또 차수가 높은 항만 취해서 나타내고
차수가 낮은 항은 무시한다.
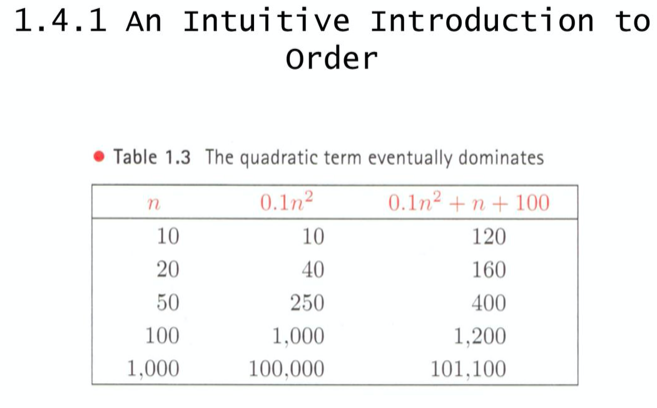
0.1 n^2이 n보다 언젠간 커진다.
asymtotic


x축은 input 사이즈, y축은 걸리는 시간과 비례

빅O의 f(n)의 정의이다.
time complexity function 들의 집합이다.
양의 실수인 상수 c가 존재하고, 음이 아닌 정수 n이 존재해서
g(n) <= c x f(n) 이다.

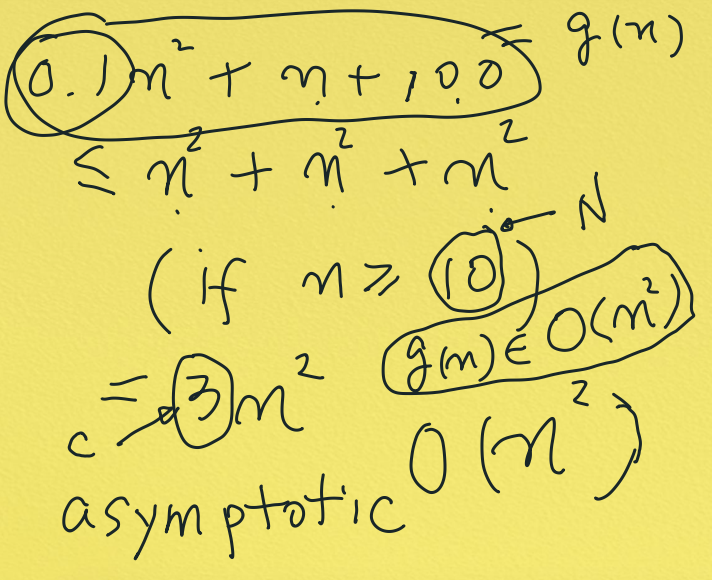
이것이 빅O의 공식적인 정의이다.
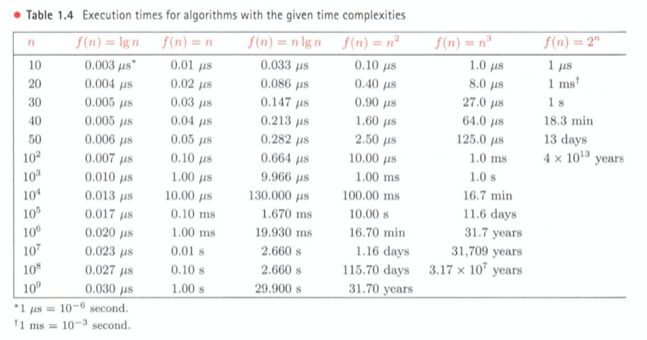
n이 조금만 커져도 n의 차수가 큰 것은 되게 오래걸린다.
써먹을 수가 없다.
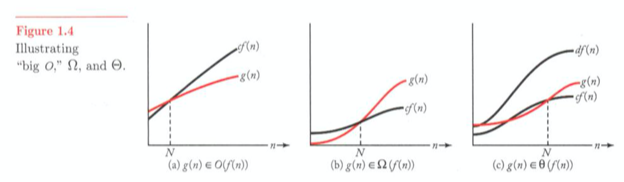
어떤 지점을 넘어선 이후로는 g(n)을 f(n)에 상수를 곱한것보다 작게 만들 수 있다.
g(n)의 증가하는 속도가 그정도다.

빅O를 asymptotic upper bound라고도 한다.
f(n)이 g(n)의 상한
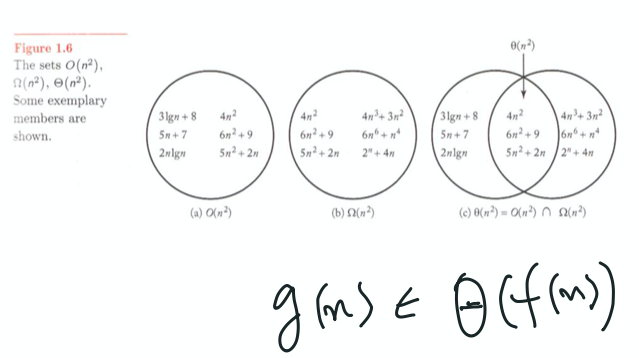
2nlog(n) 이 O(n^2)에 속한다.
2nlog(n) <= n^2 이기 때문에

이게 빅 세타의 definition이다.
g(n) is order of f(n)

T(n)의 Order는 n^2이다.
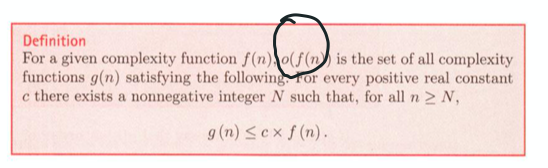
스몰 o f(n)
c가 모든 실수에 대해서 이 부등식을 성립한다.
c라는 상수가 굉장히 작은 수 일수도 있다.
그러면 g(n)이라는 함수의 오더가 f(n)이라는 함수의 오더보다 완전히 작다라는 뜻이다.
O (n^2)이라고 하면은 order가 n^2보다 같거나 작은것들이 다 속한다.
그러나 스몰 o의 (n^2)이라고 하면은 2차식은 속할 수가 없다.
2차식보다 낮은 것들만 속할 수 있다

자 다음으로 중요한게 나온다
Order의 property이다.

직관적으로 이해가 갈 것이다.
3번째 : 로그의 밑수가 1보다 크면 오더에 영향을 미치지 않는다.
log2(n) 이 log10(n) 의 빅세타에 속하고,
log10(n) 이 log2(n) 의 빅세타에도 속한다.
양쪽이 다 성립한다.

팩토리얼이 n승보다 더 크다

log(log(n))은 매우 빠르다.
7번 성질
'🕶 Algorithm > 알고리즘' 카테고리의 다른 글
| 알고리즘 과제 #1 (0) | 2020.03.28 |
|---|---|
| Divide-and-Conquer (part1) (0) | 2020.03.26 |
| Algorithms Chapter 1 (part4) (0) | 2020.03.23 |
| Algorithms Chapter 1 (part2) (0) | 2020.03.16 |
| Algorithms Chapter 1 (part1) (0) | 2020.03.16 |