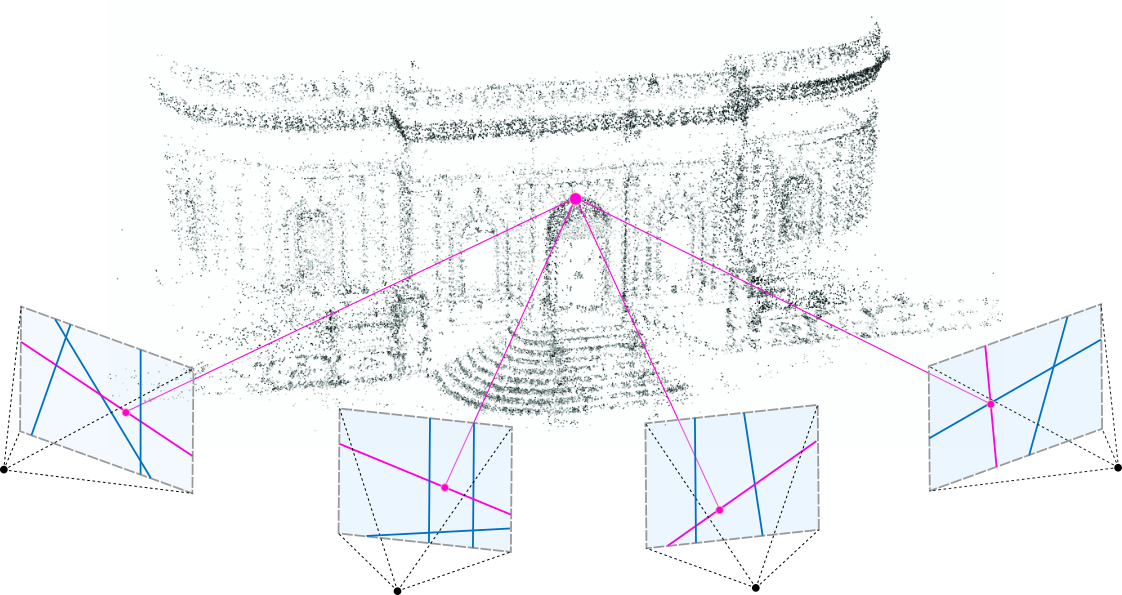

Structure from Motion
Structure from Motion은 2차원 영상으로부터 3차원 정보를 추출하여 3D로 재구성하는(structure = 3D structure, motion=Camera pose) 것을 Structure from Motion(SFM)이라고 부릅니다.

Structure from Motion은 순차적인 이미지 세트로부터 그림에서 보이는 바와 같이 Structure의 3D 재구성을 진행합니다.
3D scene structure를 어떻게 정확하게 찾아 낼 것인지, cameara pose(사진이 어디서 찍혔는지), camera intrinsic, extrinsic parameter를 어떻게 찾아낼 것인지를 알아보는 것입니다.
목차
- Camera Calibration (Intrinsic Parameters & Extrinsic Parameters)
- Feature Detection
- Description : 각 이미지 간의 서로 feature를 매칭시킴 (with SIFT)
- Epipolar Geometry : 각 feature 들의 Correspondence 대응 문제를 해결
- Triangulation : 각 Correspondence된 feature들을 3차원 포인터로 생성해 3D 구조로 만든다.
- Bundle Adjustment : 에러를 최소화
Camera Calibration
우리가 실제 눈으로 보는 세상은 3차원입니다. 하지만 이것을 카메라로 찍으면 2차원의 이미지로 변하게 됩니다. 이 때, 3차원의 점들이 이미지 상에서 어디에 맺히는지는 기하학적으로 생각하면 영상을 찍을 당시의 카메라의 위치 및 방향에 의해 결정됩니다. 하지만 실제 이미지는 사용된 렌즈, 렌즈와 이미지 센서와의 거리, 렌즈와 이미지 센서가 이루는 각 등 카메라 내부의 기구적인 부분에 의해서 크게 영향을 받습니다. 따라서, 3차원 점들이 영상에 투영된 위치를 구하거나 역으로 영상좌표로부터 3차원 공간좌표를 복원할 때에는 이러한 내부 요인을 제거해야만 정확한 계산이 가능해집니다. 그리고 이러한 내부 요인의 파라미터 값을 구하는 과정을 카메라 캘리브레이션이라 부릅니다. 카메라 내부, 외부 오차로 인해 부정확한 3D Reconstruction 이 발생할 수 있기 때문에 Camera Calibration 과정은 매우 중요합니다.
카메라 영상은 3차원 공간상의 점들을 2차원 이미지 평면에 투사(perspective projection)함으로써 얻어집니다. 핀홀(pinhole) 카메라 모델에서 이러한 변환 관계는 다음과 같이 모델링됩니다.
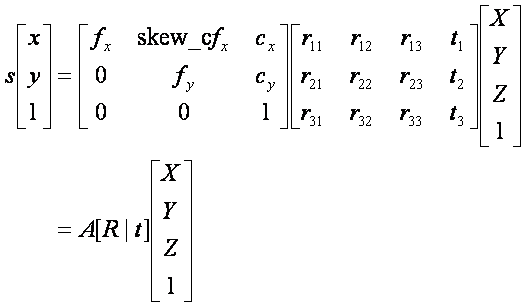
- (X,Y,Z) : 월드 좌표계(World coordinate system) 상의 3D 점의 좌표
- [R|t] : 월드 좌표계를 카메라 좌표계로 변환시키기 위한 회전/이동변환 행렬(Extrinsic parameter)
- A : 카메라 내부 파라미터(Intrinsic camera matrix)
- A[R|t] : Camera matrix 또는 Projection matrix
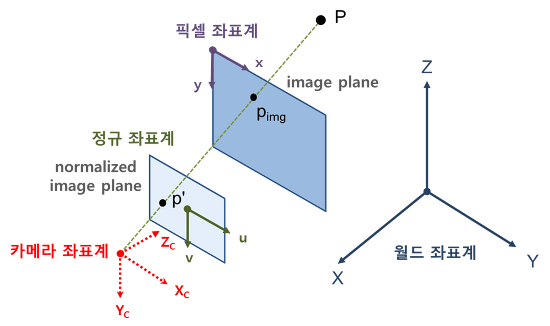
수식적으로 보면 Camera calibration은 위와 같은 3D 공간좌표와 2D 영상좌표 사이의 변환관계 또는 이 변환관계를 설명하는 파라미터를 찾는 과정입니다.
식(1)에서 [R|t]를 카메라 외부 파라미터(extrinsic parameter), A를 내부 파라미터(intrinsic parameter)라고 부릅니다. 그리고 A와 [R|t]를 합쳐서 camera matrix 또는 projection matrix라 부릅니다.
카메라 외부 파라미터는 카메라의 설치 높이, 방향(팬, 틸트) 등 카메라와 외부 공간과의 기하학적 관계에 관련된 파라미터이며 내부 파라미터는 카메라의 초점 거리, aspect ratio, 중심점 등 카메라 자체의 내부적인 파라미터를 의미합니다.
Intrinsic parameter
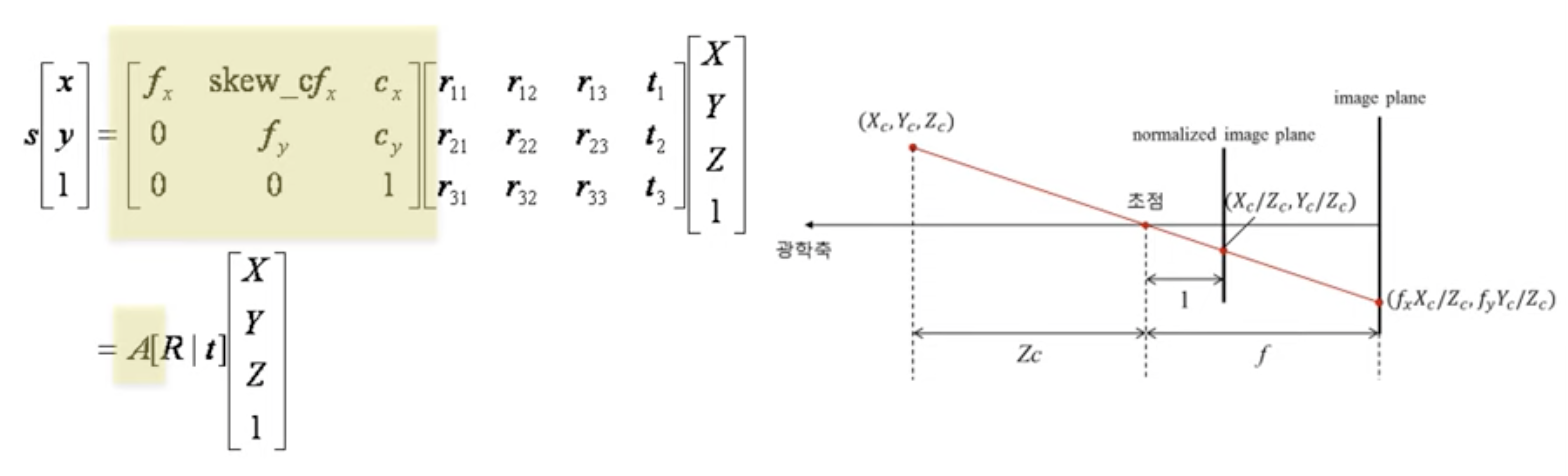
카메라의 내부 파라미터는 다음과 같은 것들이 있습니다.
- 초점 거리 (focal length) fx, fy : 렌즈 중심과 이미지 센서와의 거리, 픽셀 단위로 표현
- 주점 (principal point) cx, cy : 카메라 렌즈의 중심
- 비대칭 계수 skew_c : 이미지 센서의 y축이 기울어진 정도
내부 파라미터(Intrinsic parameter)란 최초 카메라 공정 과정에서 결정되는 파라미터를 말합니다. 여기서 가장 중요한건 초점거리인 focal length입니다. 렌즈 중심과 이미지 센서(CCD,CMO 등)와의 거리를 말합니다. 주점인 cx와 cy는 카메라 렌즈의 중심을 말하며, 비대칭 계수는 픽셀의 y축 기울어진 정도를 나타내지만, 최신 카메라는 skew 에러가 없기 때문에 이것까지는 고려하지 않습니다. 따라서 이러한 값이 담긴 파라미터 행렬은 A로 표현됩니다.
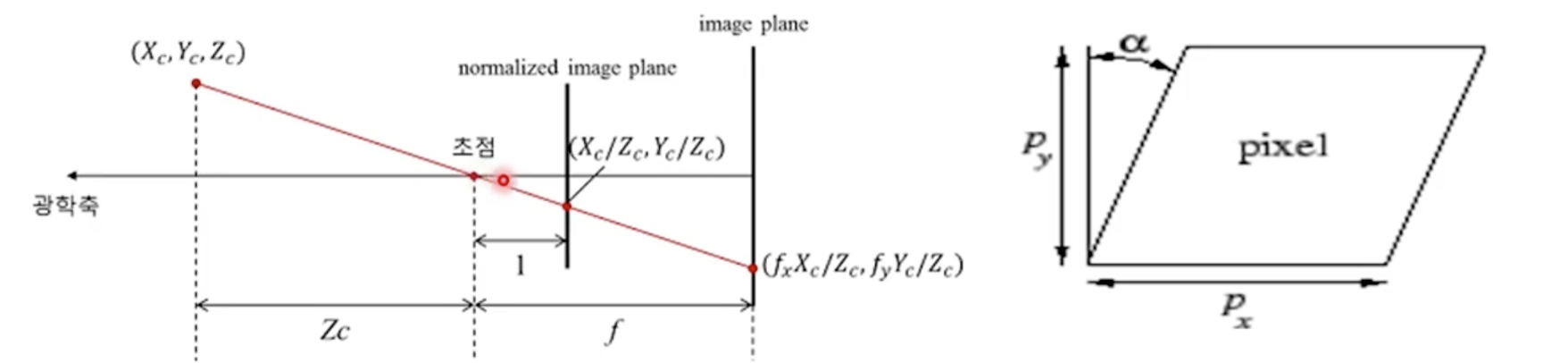
핀홀 모델에서 보았듯, 초점과 상이 맺히는 곳까지의 거리가 상이 어떻게 맺히는 지를 알려주게 됩니다. 즉, 초점으로부터 상이 맺히는 거리가 멀수록 물체가 크게 맺히겠지만 해상도는 조금 떨어집니다. 반면에 초점거리가 짧으면 크기가 작게 맺히면서 해상도가 높아지는 효과가 있을 것입니다. 이처럼 초점 거리를 구하는 것이 굉장히 중요합니다.
위 사진은 초점거리를 1로 맞췄을 때의 예입니다. 보통 초점 거리를 f라고 합니다. f라는 값을 추정해야만 3차원 점이 영상 상의 어떠한 점에 투영되는 지를 확인할 수 있습니다. X,Y,Z라는 점이 (fx Xc / Zc, fy Yc / Zc)라는 점으로 투영이 되는데, 이렇게 투영이 되는 값은 어떻게 계산할까요? 아주 간단하게 비례식으로 계산이 된다. 양 삼각형이 서로 닮음이기 때문에 간단히 구할 수 있습니다.
카메라 센터로부터 반직선을 정의할 수 있는데 보통 광학축이라고 합니다. 광학축이 영상에 미치는 공간(image plane)과 통과되는 위치가 있을 것입니다. 그 통과되는 좌표를 보통 principal point라고 합니다. 그 외에는 픽셀이 사각형의 형태로 생겨야 하는데 공정상의 문제로 평행사변형 같이 생기는 경우가 있습니다. 그래서 이 값을 반영해서 비대칭계수라는 것도 구해야 하는데, 요즘에는 공정이 정확해져서 비대칭계수는 0이라고 봐도 무방합니다.
Extrinsic parameter
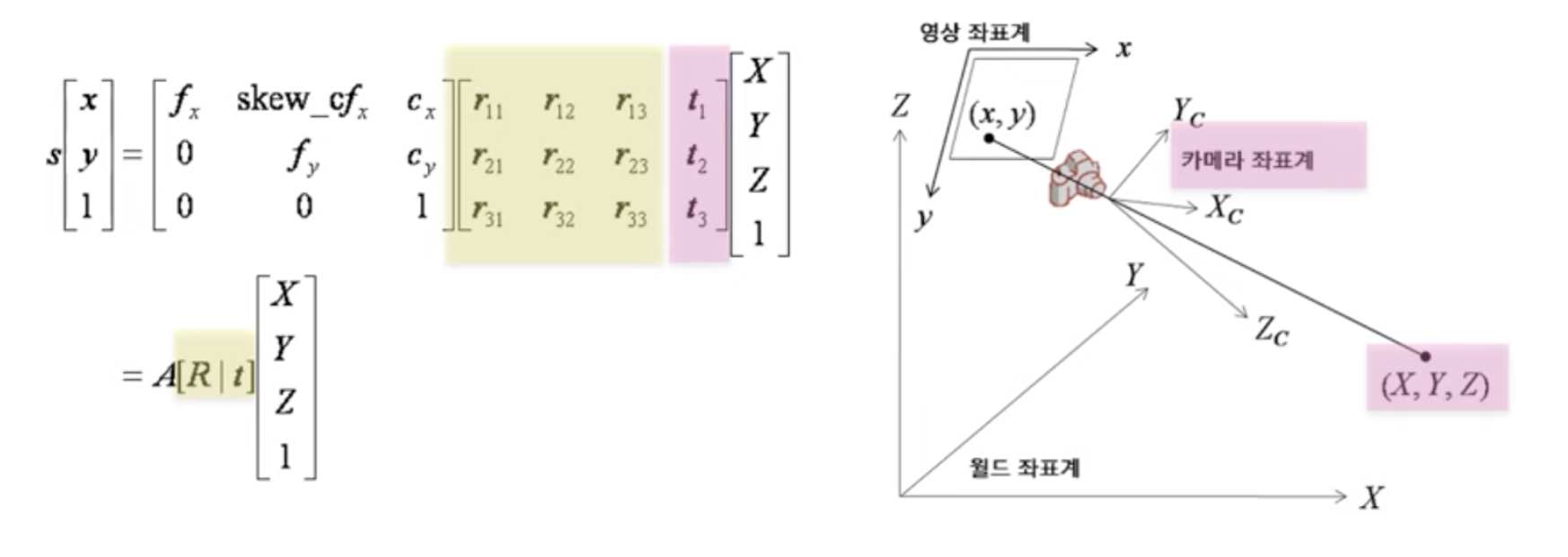
카메라를 항상 동일한 위치에서 촬영하는 것이 아닙니다. 카메라의 위치와 카메라가 어디를 바라보느냐에 따라 3차원 점이 픽셀에 투영되는 위치가 달라지게 됩니다. 이 부분을 외부파라미터라고 합니다. 외부 파라미터(extrinsic parameter)는 3차원 월드 좌표계에서 카메라의 위치를 설명해줍니다. 카메라가 원점으로부터 얼마나 떨어져 있는지, 어떠한 각도로 회전되어 있는지를 설명합니다. 즉, 외부 파라미터는 카메라 좌표계와 월드 좌표계 사이의 변환 관계를 설명하는 파라미터로서, 두 좌표계 사이의 회전(rotation) 및 평행이동(translation) 변환으로 표현됩니다.
외부파라미터는 오른쪽 그림의 월드좌표계 Large X,Y,Z와 카메라 좌표계 간의 상대적 위치를 정의하는 것입니다.
따라서 영상을 획득한 당시의 카메라 위치관계를 설명하고 좌측 노란박스를 보시면 r로 표기된 3x3 행렬이 얼마만큼 회전을 나타내는가 하는 Rotation 행렬을 나타냅니다.
오른쪽측 분홍색 박스가 카메라가 실제 원점으로부터 얼마만큼 이동 되었는지에 대한 translation 행렬을 나타냅니다. 이 카메라 Calibration 값은 이후 소개될 Epipolar Geomtry에서 다시 한번 등장하게 됩니다.
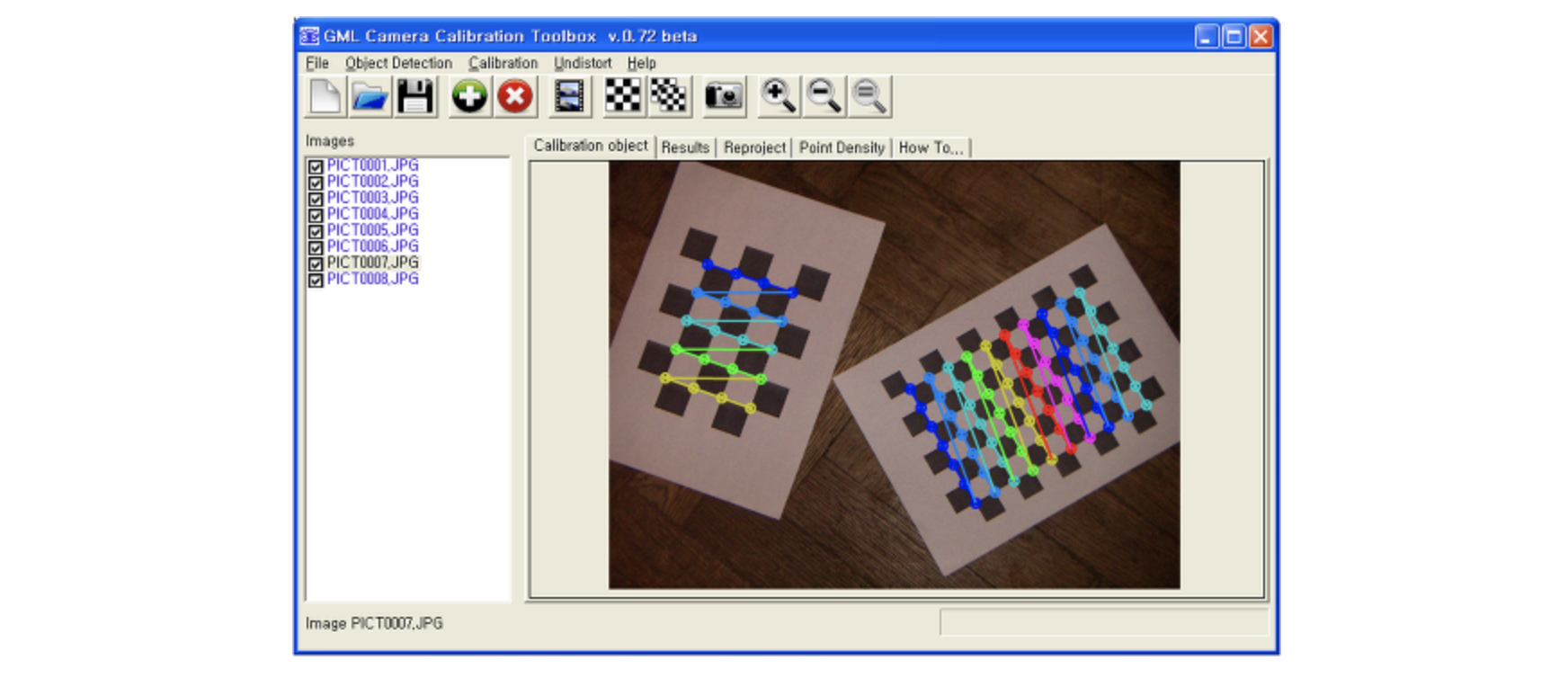
이러한 파라미터를 구하는 클래식한 방법은 체크 패턴을 이용하는 것입니다. 패턴의 특징점을 추출해보면 경계 부분에서 피쳐들이 많이 추출되는 것을 볼 수 있습니다. 이 피쳐들이 3차원 공간의 어디에 있는지를 추정할 수 있습니다.
패턴의 왼쪽 위를 월드좌표계의 원점이라고 정의하면, 패턴의 실제 크기를 알고 있기 때문에 각각의 꼭지점의 위치를 알 수 있습니다. 그러면 우리가 추출한 피쳐들의 3차원 좌표들을 알고 있는 것이고 이 패턴을 실제로 촬영했기 때문에 영상상에서 피쳐들을 추출하게 되면 2차원 좌표도 알고 있는 것입니다. 즉, 3차원 점이 어떠한 위치로 맵핑이 되었는가를 2차원 영상좌표와의 매칭 쌍을 알수 있게 되는 것입니다.
Feature Detection

Feature Detection에서는 영상 내부의 작은 영역이 모든 방향에 대해 변화가 큰 경우 코너로 규정해 각 특징점들을 추출해줍니다. 하지만 영상의 이동, 회전, 크기 변환에 취약한 문제가 있었습니다.

그래서 이를 해결하기 위해 Difference of Gaussian기법을 사용하는 Scale-Space 기법과 Image Pyramid 형태로 다양한 크기 관점에서 특징 검출을 해줌으로써 이전문제를 보완해주었습니다.
이러한 기법이 적용되고 발전한 SIFT SURF, BRISK, ORB, FAST 등 다양한 Feature Detection 기법이 있습니다.

위 그림은 SIFT Feature Detection 기법을 사용하여 에펠탑의 특징들을 추출한 그림입니다. SIFT는 나온지 20년이 넘었음에도 여전히 많이 사용되고 있는 Feature Detection 기법입니다. 두 이미지 간의 추출한 feature들의 벡터 히스토그램을 생성하는 것이 Feature Description입니다.
Feature Description
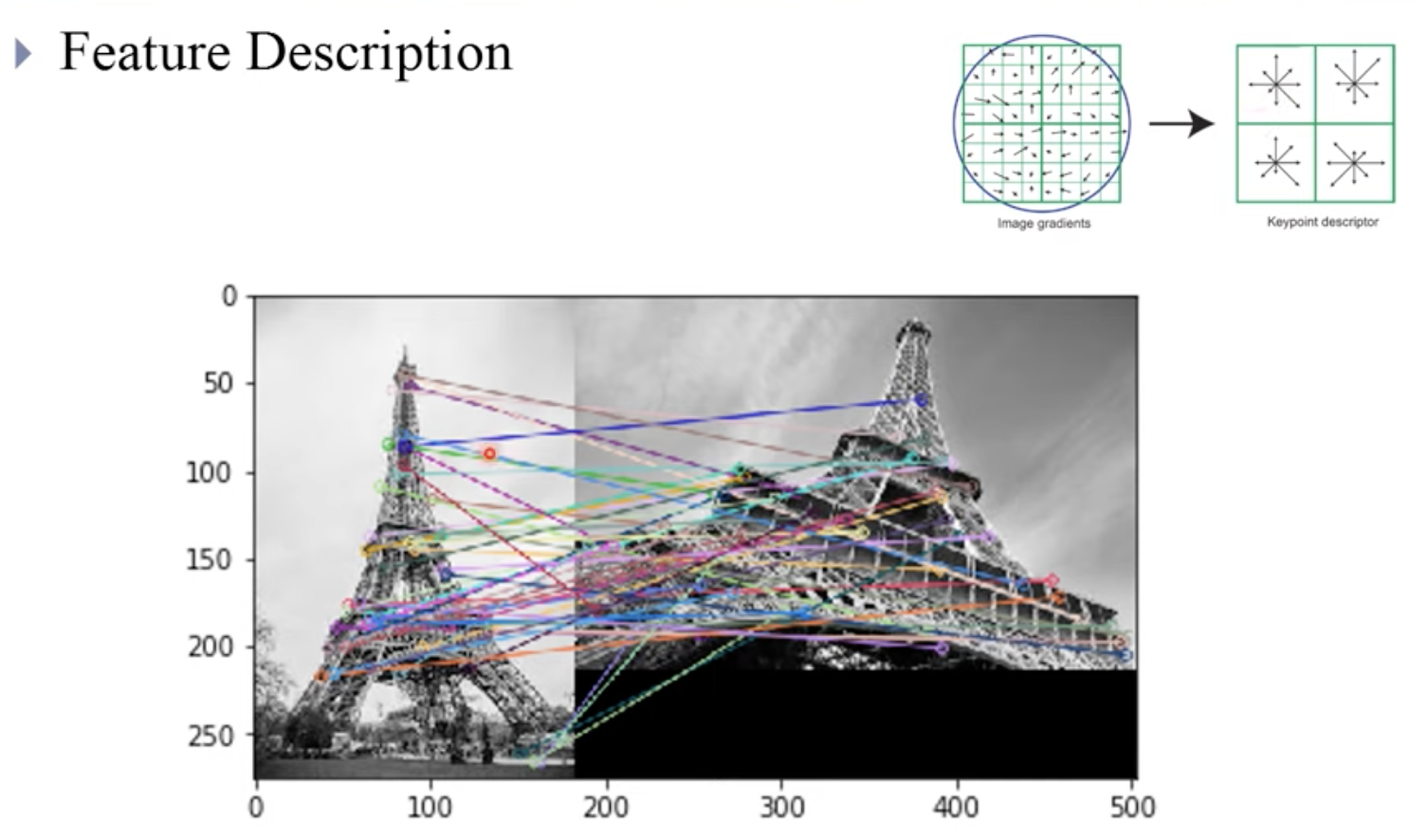
오른쪽 위의 그림이 벡터 히스토그램입니다. 그 후 각 Feature들 간의 높은 유사도를 가지는 Descriptor끼리 매칭시켜줍니다.
하지만 여기에는 현재 틀린 것도 있고 맞는 것도 있습니다. 이러한 feature간의 대응관계를 Correspondence 라고 합니다.
이 문제를 해결해주기 위해 다음 Epipolar Geometry를 다루게 됩니다.
Epipolar Geometry

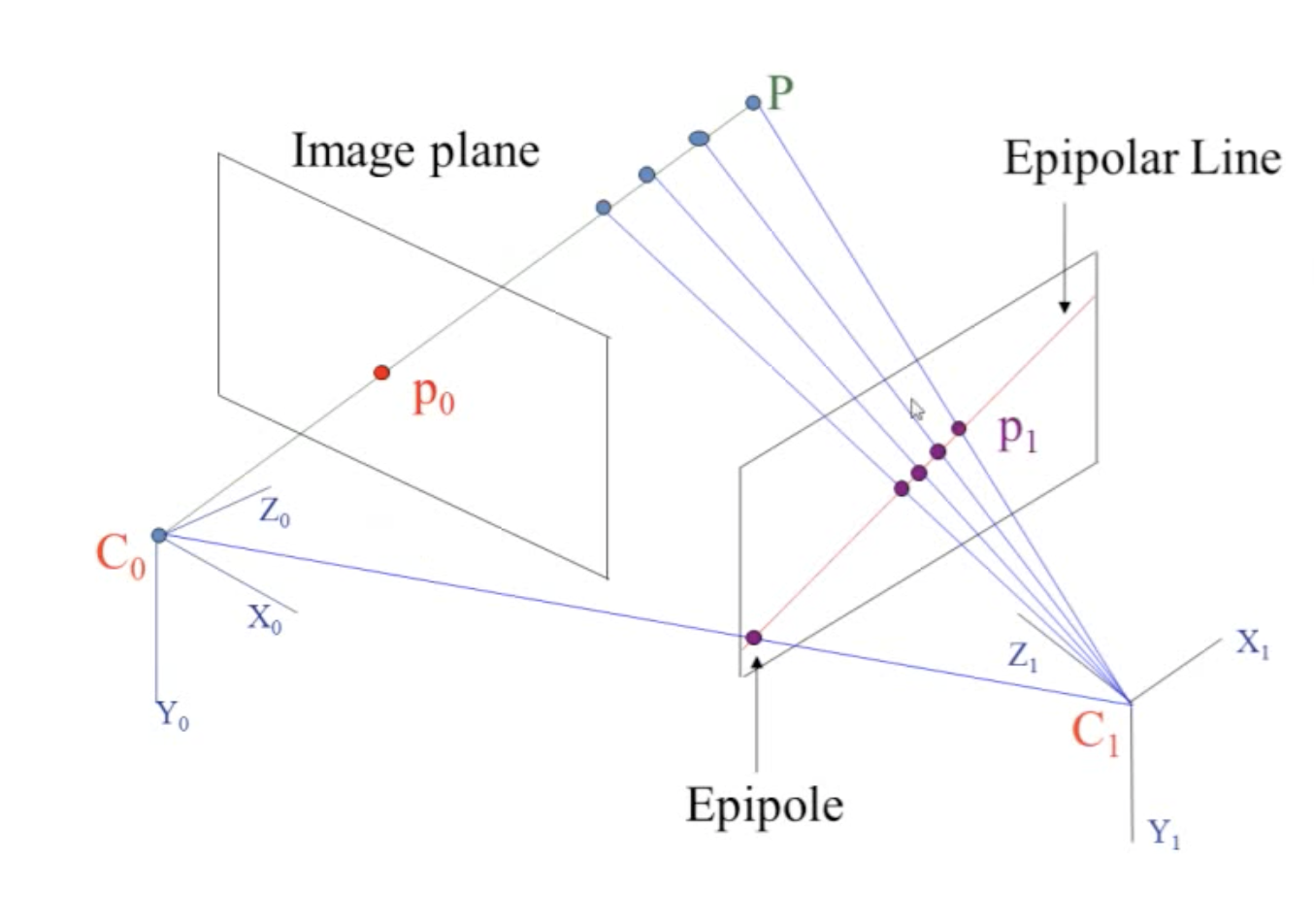
이전에 추출하였던 두 이미지안의 feature들의 대응관계인 correspondence 를 해결해주기 위해서는 Epipolar Geometry가 필요합니다. Epipolar geometry는 스테레오 비전(stereo vision) 즉, 2-view 비전에서의 기하라고 생각하면 됩니다.
즉, Epipolar geometry는 동일한 사물 또는 장면에 대한 영상을 서로 다른 두 지점에서 획득했을 때, 영상 A와 영상 B의 매칭쌍들 사이의 기하학적 관계를 다루는 것입니다.
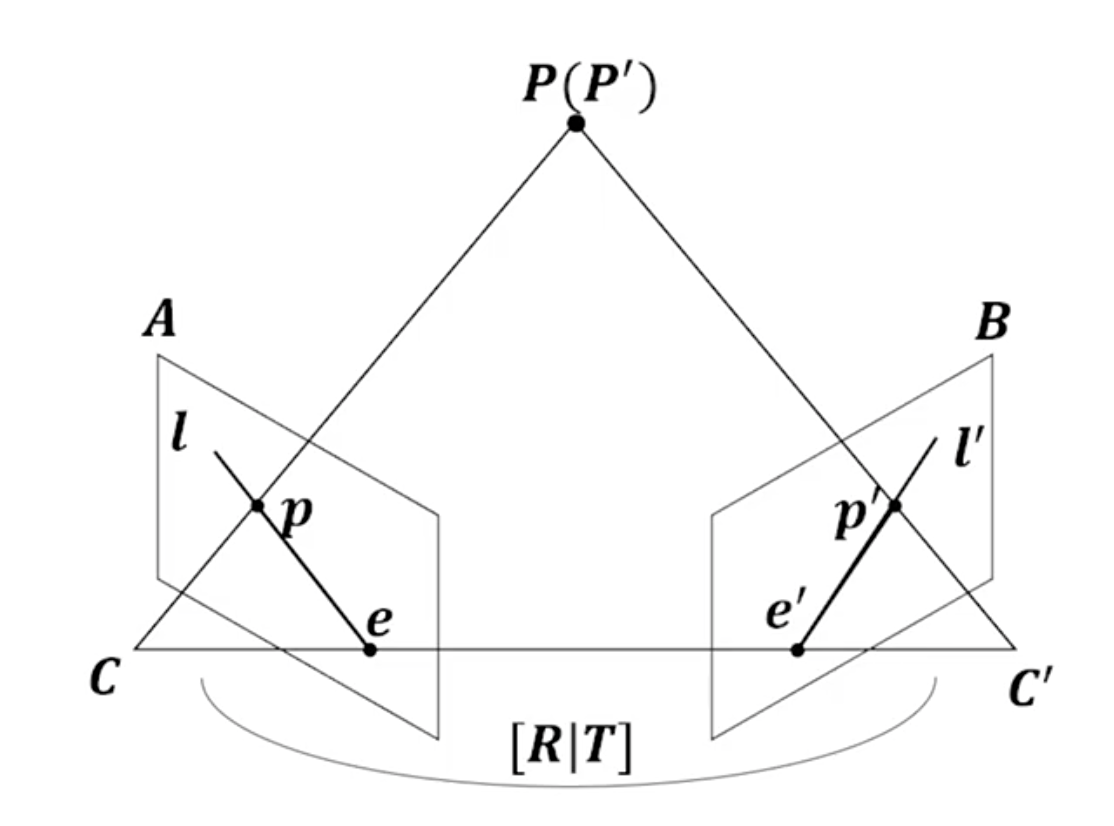
결국 카메라라는 것은 3차원 공간의 물체를 2차원 공간으로 투영하는 것입니다. 어떤 물체(P)가 있을 때, 물체를 바라보고 있는 카메라가 두개가 있습니다. P는 p와 p' 으로 투영이 됩니다. 이럴 때, 동일한 사물을 서로 다른 두 카메라로 획득했을 때, 매칭 쌍(p와 p')간의 관계를 나타내는 것이 Epipolar geometry 입니다.
먼저 각 기호가 무엇을 뜻하는 지 알고 갑시다.
- P(P') : 이미지 상에 맺힐 3차원 공간 상의 점
- C(C') : 각 영상을 촬영한 카메라의 센터
- p(p') : P가 projection 됐을 때 발생한 점, 이미지 상의 점
- e(e'), Epipole : 다른 카메라의 센터가 해당 영상의 이미지 상에 맺히는 점 (C'을 A에 투영했을 때 e가 만들어짐)
- l(l'), Epipole line : e와 p를 잇는 선
- Baseline : 두개의 카메라 사이의 거리
- [R|T] : C카메라 센터를 기준으로 C'이 얼마나 Rotation과 Translation이 됐는지를 나타내는 Matrix
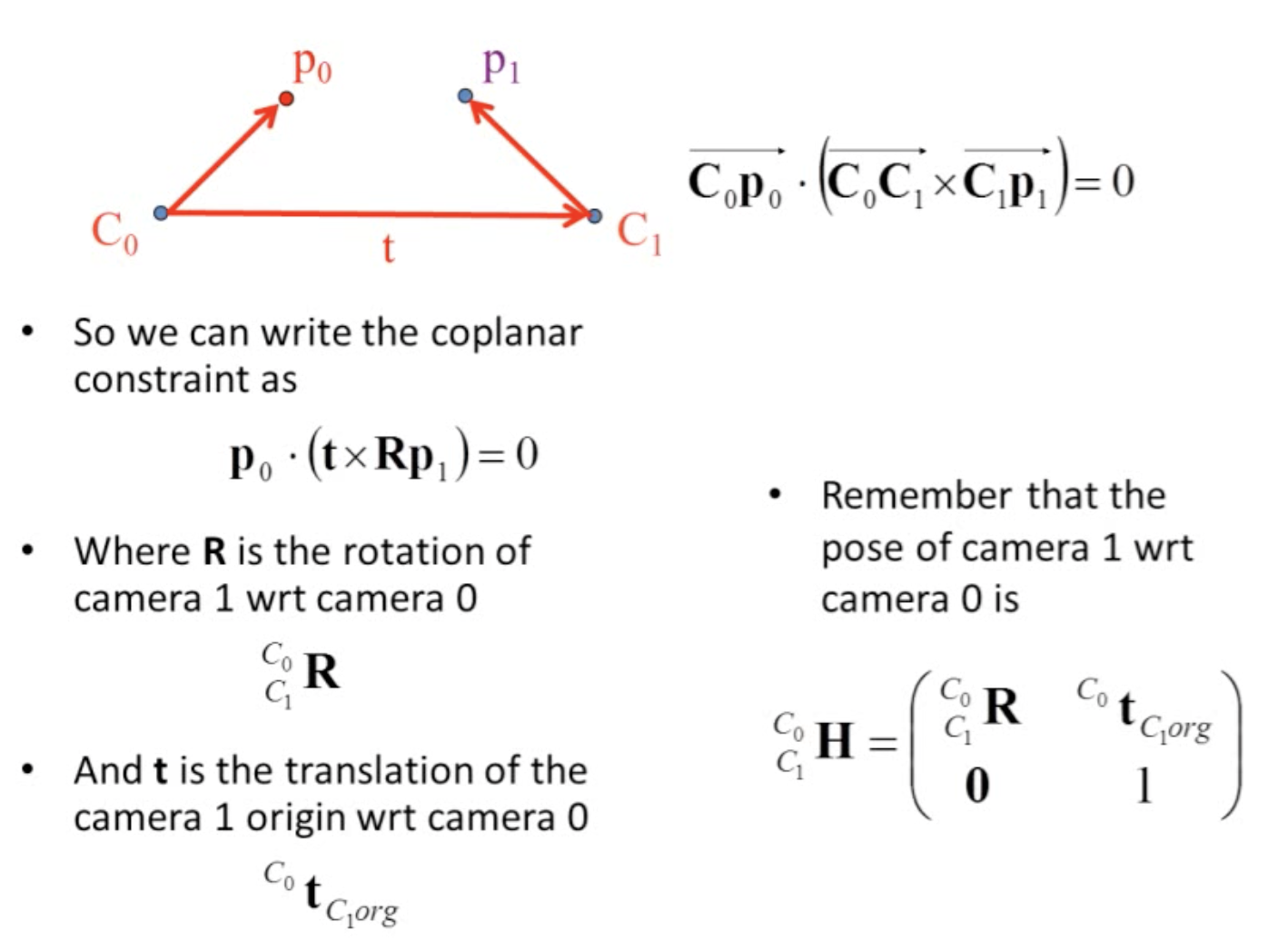
여기서 [R|T]와 p를 알더라도 3차원 공간상의 점 P에 대한 실제 깊이(depth)값을 알지 못하면 p'을 정확하게 알 수 없습니다. 왜냐면 위 그림 상에서 P의 위치를 정확하게 알고 있지만 p 만으로는 P의 위치를 정확하게 알 수가 없습니다. 따라서 유일한 P'을 결정할 수가 없습니다.
P와 p를 잇는 직선인 Ray를 B로 투영시키면 l'(Epipolar line)이 됩니다. 즉, 우리가 2개의 view와 이미지와 2개의 카메라 간의 위치 관계를 안다면 점과 점을 대응시킬 수는 없지만, 점과 선을 대응시킬 수는 있습니다. 그래서 점과 선의 관계를 나타내는 행렬을 정의할 수 있는데, 그 행렬을 우리는 Fundamental Matrix 또는 Essential Matrix 라고 부릅니다.
정리하면, 'A의 영상 좌표 p로부터 대응되는 B의 영상 좌표 p'을 유일하게 결정할 수는 없지만, p'이 지나는 직선인 epiline l'은 유일하게 결정할수 있다' 입니다. 그리고 한 영상 좌표로부터 다른 영상에서의 대응되는 epiline을 계산해주는 변환행렬이 Fundamental Matrix, Essential Matrix 입니다. 즉, 서로 다른 두 시점에서 찍은 영상 좌표들 사이에는 Fundamental Matrix, Essential Matrix를 매개로 하는 어떤 변환 관계가 성립하는데, Epipolar Geometry에서는 이 변환관계를 바탕으로 여러 기하학적 문제를 풀게 됩니다.
3D 공간상의 한 점 P가 영상 A에서는 p에 투영되고, 영상 B에서는 p'에 투영됐다고 하면 두 영상 좌표 p와 p' 사이에는 다음 관계를 만족하는 행렬이 항상 존재한다는 것이 epipolar geometry의 핵심입니다 (단, p, p'은 normalized 이미지 평면에서의 homogeneous 좌표임).
Fundamental Matrix와 Essential Matrix에 대한 자세한 설명
앞서 설명한 Essential Matrix는 정규화된 이미지 평면에서의 매칭 쌍들 사이의 기하학적 관계를 설명하는 행렬입니다. 즉, 카메라 내부 파라미터 행렬인 K가 제거된 좌표계에서의 변환관계입니다.
반면 Fundamental matrix는 카메라 파라미터까지 포함한 두 이미지의 실제 픽셀(pixel) 좌표 사이의 기하학적 관계를 표현하는 행렬입니다.
Triangulation
지금까지 저희는 두 이미지간 feature의 correspondence를 추정해주었고 아직 3D points location은 알지 못합니다. 그러기 위해선 Triangulation , 즉, 삼각법을 사용해야 합니다.
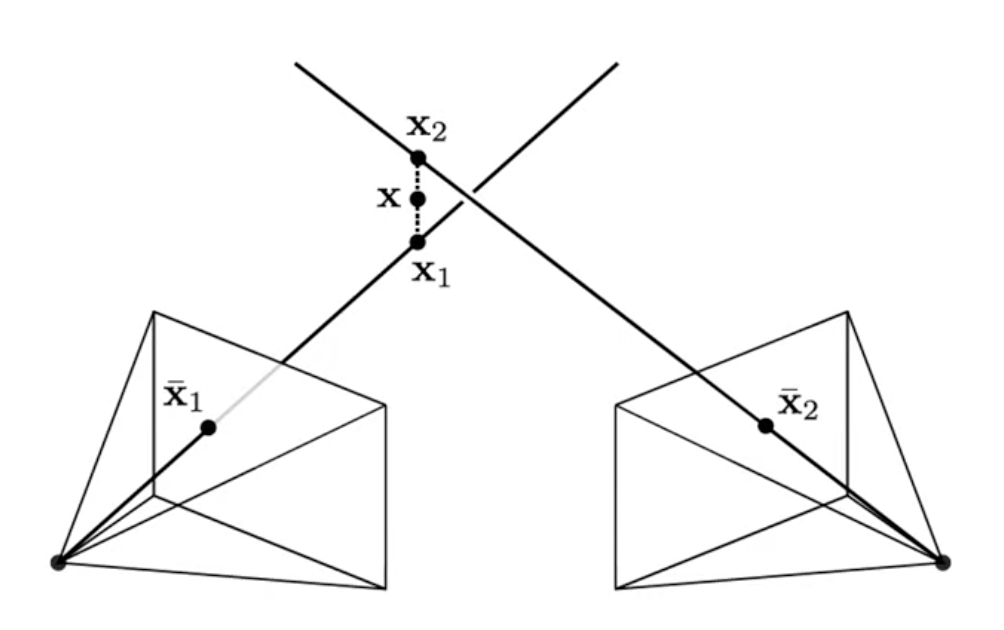
현재 보이시는 그림에서 x1과 x2는 두 2D 이미지 상에서 관찰하는 위치가 됩니다. 만약 전혀 오차가 없는 상황이라면 x1과 x2는 일치할 것입니다. 그리고 x1와 x2를 연결하여 중점인 x를 구하게됩니다. 이러한 방식으로 3D point를 구하게 됩니다.
Triangulation Uncertainty
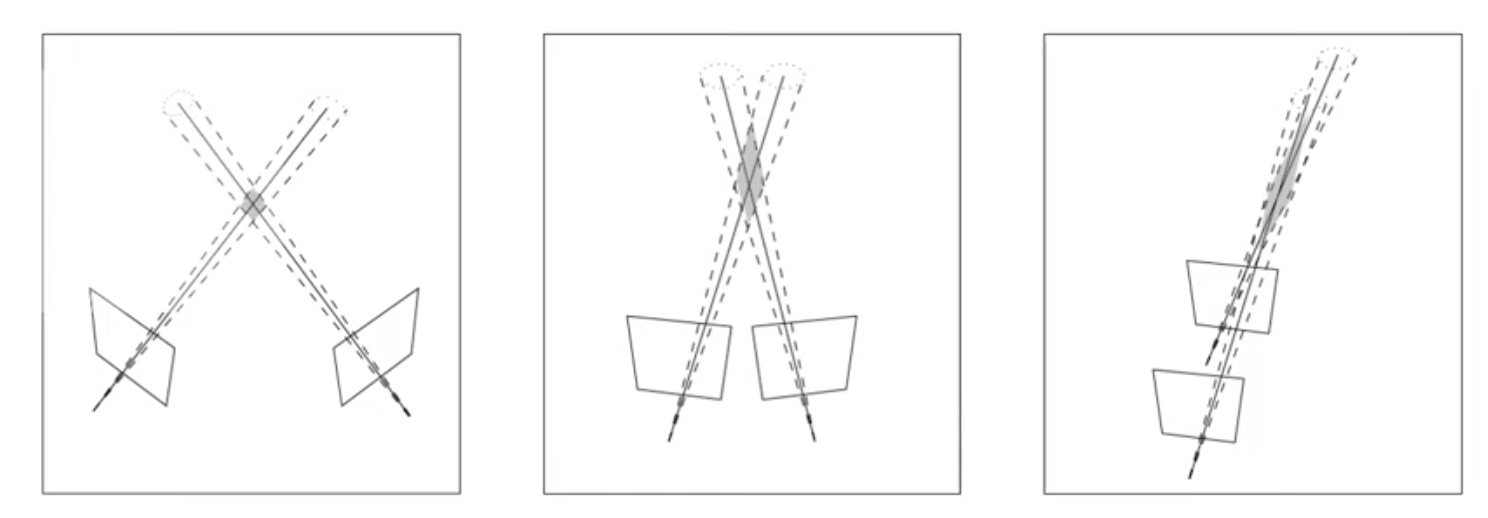
3D 좌표를 추정할 때 두 이미지간의 위치 관계가 어떻게 위치하느냐에 따라 Trade-off 관계가 있습니다. 가운데 보시면 마름모 위치가 3D point가 위치할 곳입니다. 각 이미지에서 관찰하는 좌표의 오차가 존재하기 때문에 크로스 되는 곳이 점이 아닌 마름모 형태를 띄게 됩니다.
좌측같은 경우에 이미지 간의 관계가 겹치는 부분도 없고 거리가 멀다면, 이미지 자체가 꽤 다른 모습을 보이고 있기 떄문에 feature matching하기가 어렵다는 단점이 있습니다. 하지만 삼각법에서는 좀더 좋은 성능을 보이고 있습니다.
그에 반면, 이미지가 연속적인 프레임인 경우 상당 부분이 많이 겹칠 수 있습니다. 제일 오른쪽 그림의 경우 이미지가 서로 매우 유사하기때문에 feature를 매칭하기 좀 더 쉽다는 장점이 있지만, 보시는 바와 같이 마름모 영역이 늘어져 있기 때문에 삼각법을 통해 매칭하기가 다소 어려운 점이 있습니다.
Bundle Adjustment
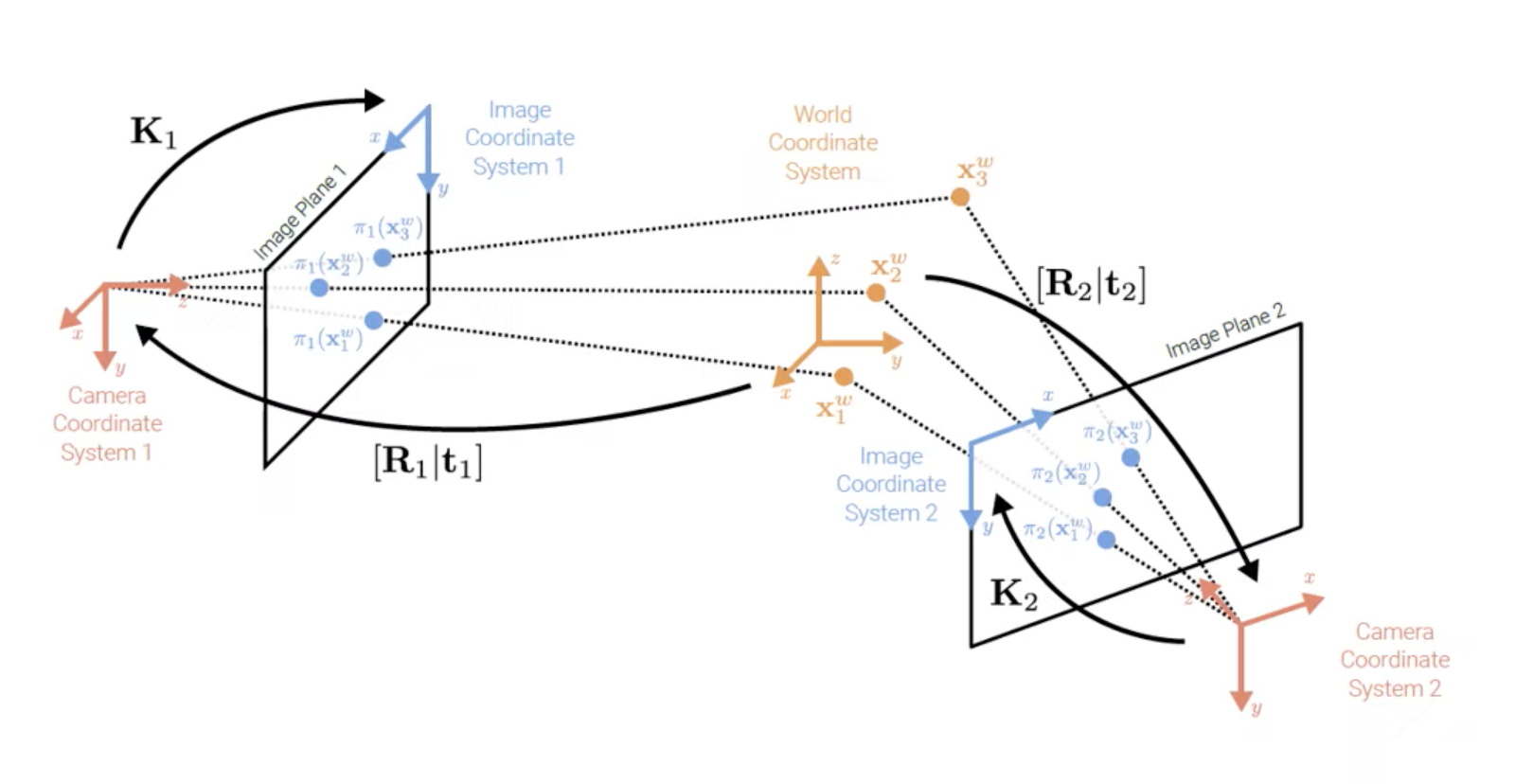
Bundle Adjustment는 다수의 프레임에 존재하는 Visual keypoint 들의 위치 (i.e. 2D pixel location)를 기반으로 추정할 수 있는 3D landmark position과 카메라 프레임간의 3D relative motion을 동시에 최적화하는 과정입니다. 즉 3차원 점들을 보다 정교하게 만드는 과정에서 사용됩니다.
위 보이는 그림은 오리지날 좌표가 아닌 삼각법을 통해서 생성한 3D 좌표를 다시 2D 이미지 상에 reprojection 시켜주었을때 파란색으로 표시되는 좌표를 보여줍니다. 이것은 실제 3D 좌표로 부터 projection되는 좌표와 함께 Bundle Adjustment를 통해 reprojection된 좌표를 비교해 error를 최소화 해줍니다. 여기서 error(reprojection error)는 3D point들을 키프레임 이미지들에 투영시킨 위치와, 해당 영상 프레임에서 실제 관측된 위치의 차이를 말합니다.
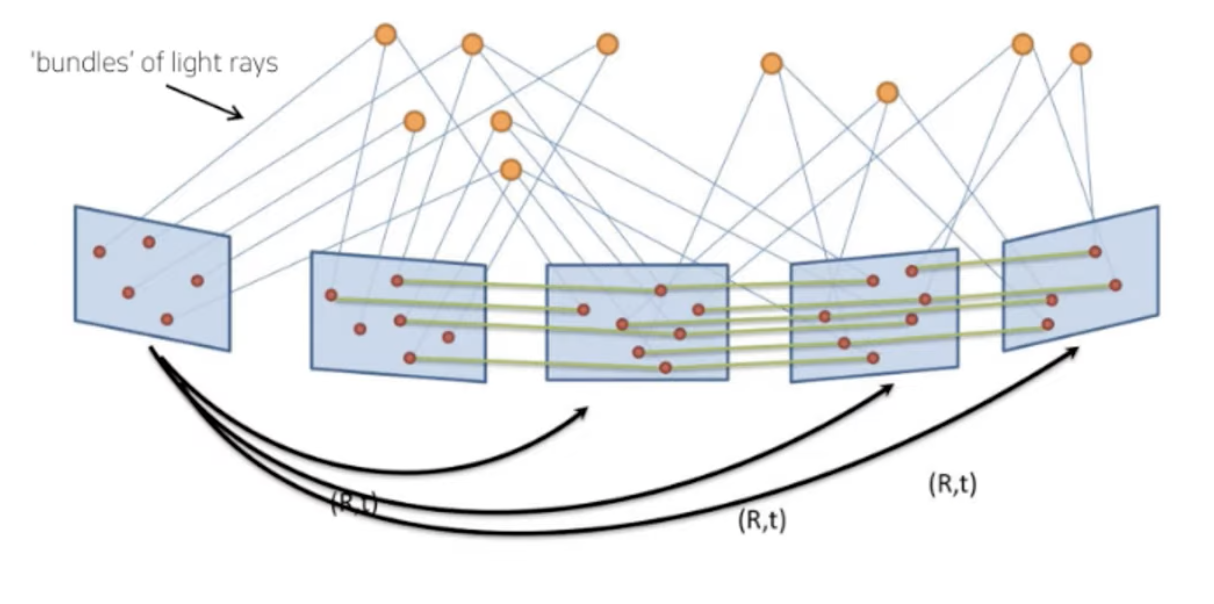
그리고 지금껏 2장의 이미지만을 봐왔지만 아래 그림처럼 실제로는 여러 개의 이미지안의 feature들의 ray들은 bundle로 묶여 있음을 확인하실 수 있습니다.
Bundle Adjustment Flow Chart
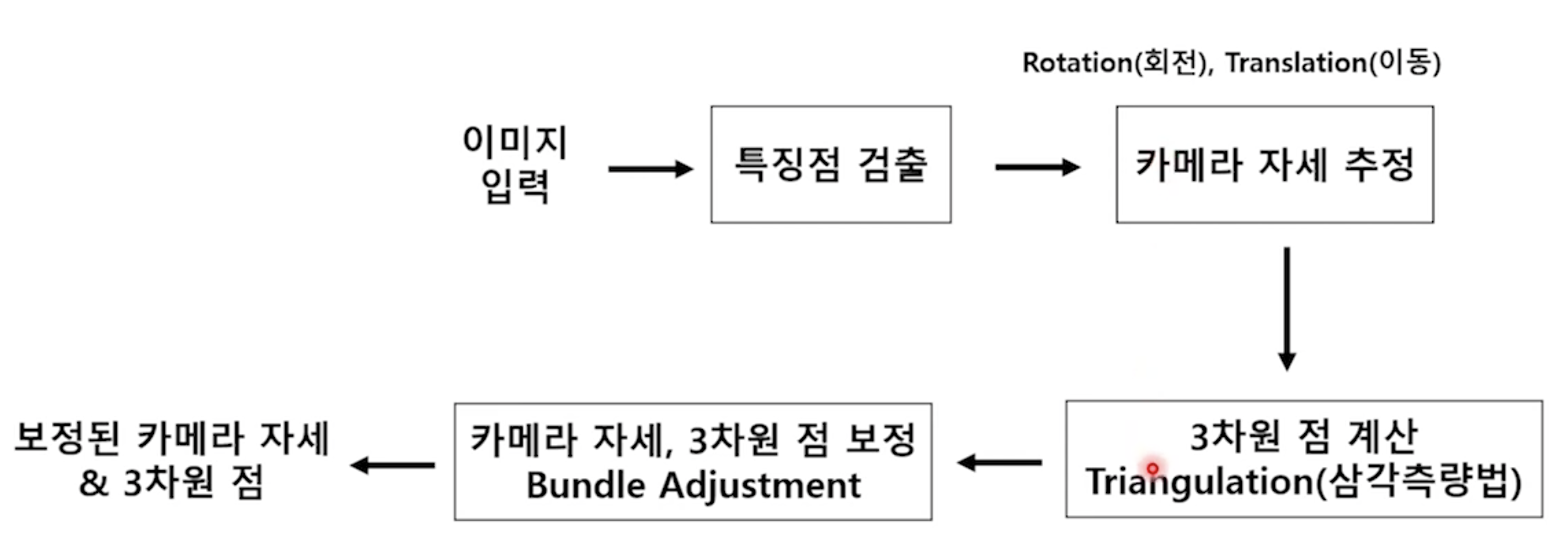
먼저 영상이 주어지면 여기서 특징점이 추출이 되고, 이것으로부터 카메라 자세를 추정할 수 있습니다.
그리고 특징점과 카메라 자세로부터 3차원 점을 만들어낼 수 있습니다.
그리고 이렇게 만들어낸 점의 위치와 카메라 자세를 보정하기 위해서 Bundle Adjustment를 활용합니다.
이 과정이 끝나면 보정된 카메라 자세와 3차원 점을 얻을 수 있습니다.
Reprojection error
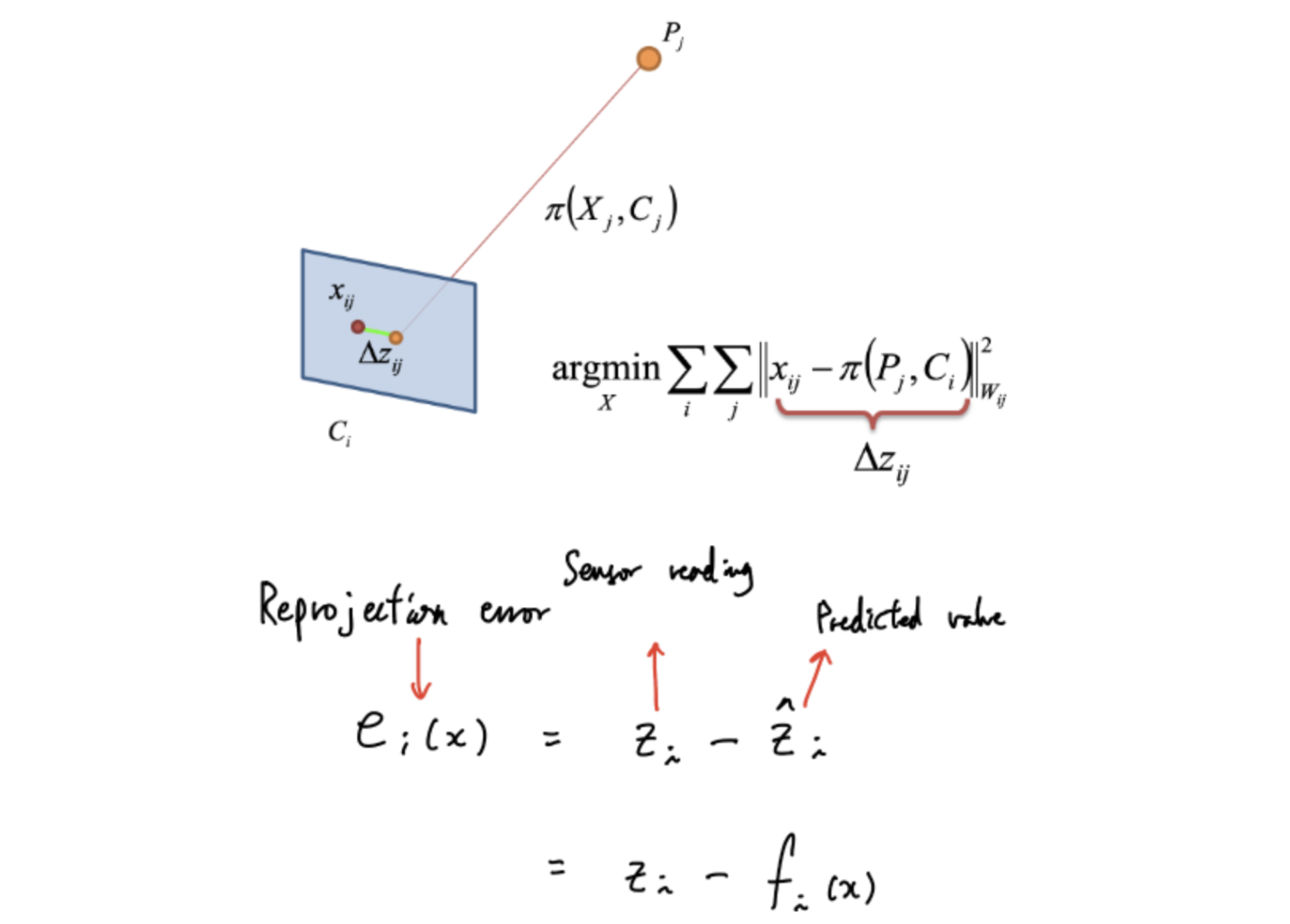
2D visual keypoint 위치가 x, 3D landmark 위치가 P, 3D camera pose가 C, projection 과정이 ㅠ일 때, reprojection error는 위와 같이 표현됩니다.

우리가 구해야하는 parameter는 3D point 인 M(X, Y, Z), 소문자 m은 3D point의 M과 대응되는 Image에서의 좌표를 말하며 Proj(M)이 3D point를 2D image로 Coordinate로 projection되는 것을 말합니다.
여기 Proj(M)에 사용되는 파라미터는 Calibration Matrix인 K가 있으며 Rotation Matrix와 translation Vector가 있습니다. 따라서 3D point가 2D 이미지로 Projection 된 좌표와 실제 3D point가 2D Image로 Projection된 좌표 사이를 줄이는 방식으로 에러를 줄이게 됩니다.
Bundle Adjustment 이후 만약 20개의 feature가 matching이 되었다고 가정해봅시다. 이것 역시 완벽히 정확하지는 않을겁니다. 그래서 또 한번 calibration 과정을 통해 R|t를 구해줍니다. Calibration을 해주기 위해서는 최소 8개의 feature matching을 해줍니다. 그래서 20개의 feature matching 해준 것에서 8개를 추출합니다
이 8개를 통해 R|t를 구하고 다시 20개와 비교를 합니다. 이때 얼마큼 정답과 맞는지 비교합니다. 만약 12개가 매칭됐으면, 다시 8개를 랜덤으로 추출해 다시 R|t를 구하고 다시 20개와 비교합니다. 이때 16개가 매칭됐습니다. 이러한 과정을 반복해서 가장 매칭 개수가 높은 것에 해당하는 R|t를 최종 R|t로 사용하게 됩니다. 이 과정을 통해 Outlier를 걸러내줍니다. 이 과정을 통해 Outlier 즉 거짓 정보를 걸러 주게 됩니다. 이것이 RANSAC입니다.
ORB SLAM에서의 Bundle Adjustment
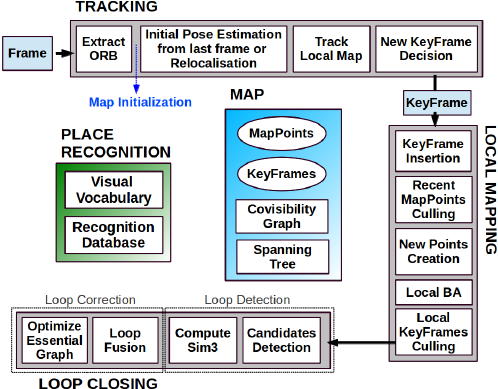
ORB SLAM에서는 총 3개의 쓰레드에서 Bundle Adjustment가 사용되는데, 사용되는 형태가 조금씩 다릅니다.
Tracking에서는 카메라 위치만을 고려한 Bundle Adjustment가 진행되고, Local Mapping에서는 3차원 지도의 전체가 아닌 일부만 활용해서 Bundle Adjustment가 수행되고, Loop Closing에서는 3차원 지도 전체를 활용한 Bundle Adjustment가 진행됩니다.
Motion only BA
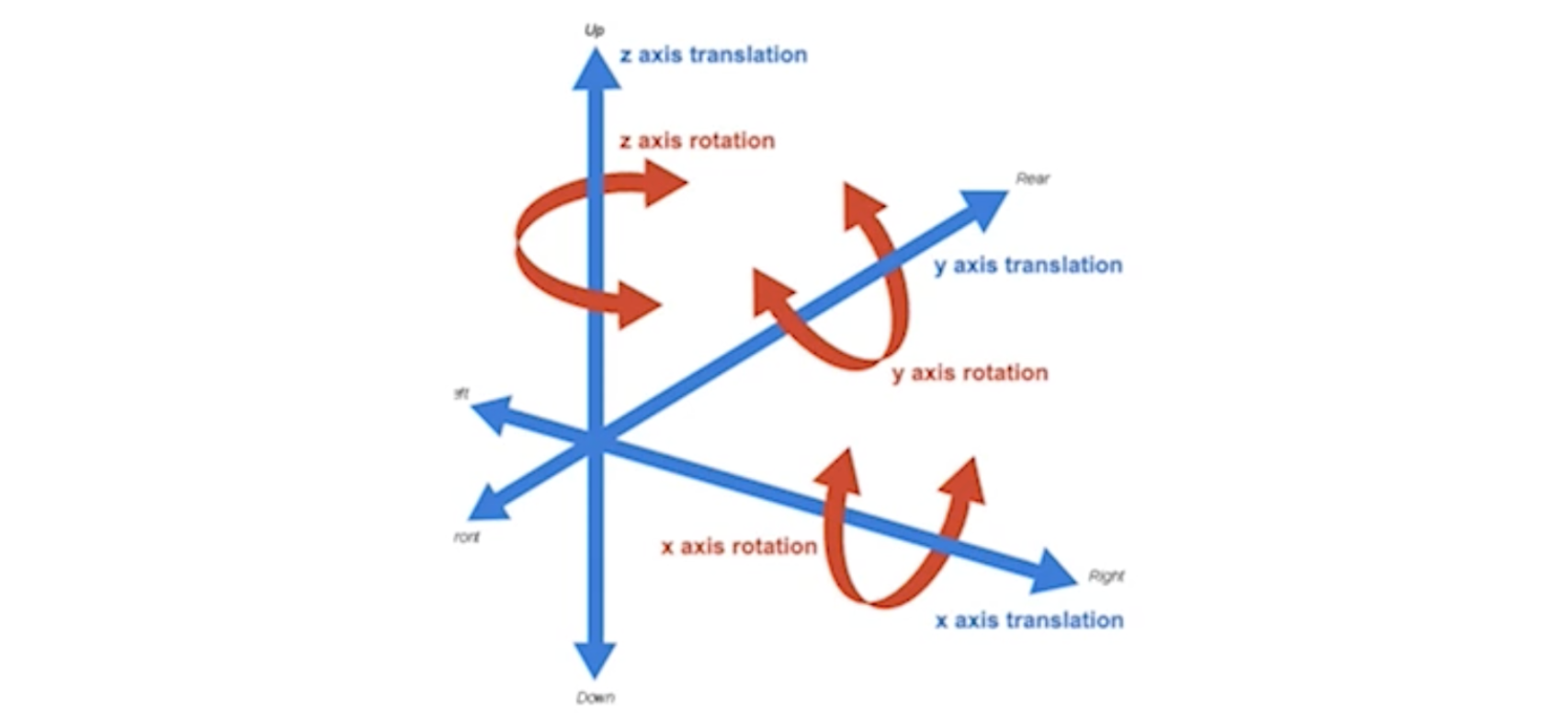
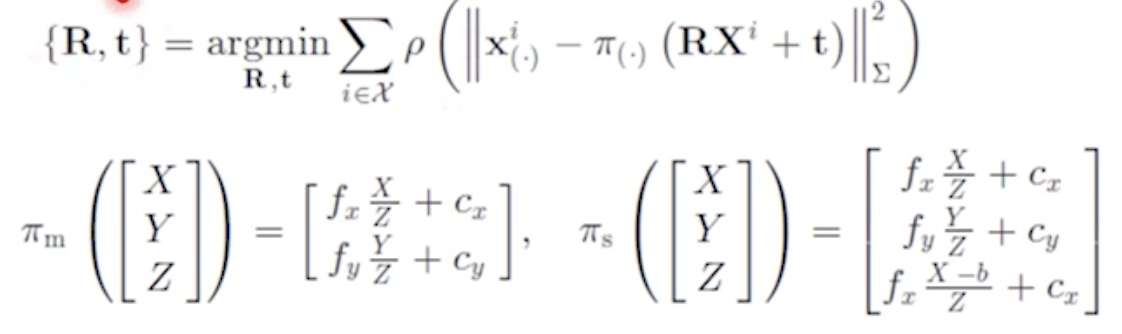
카메라의 위치만 보정하는데에 사용되는 식은 다음과 같습니다. 보시다시피 얻어지는 파라미터는 Rotation과 Tranlation이 있습니다. 영상상에 존재하는 2차원 점인 xi가 있고, 3차원 점을 카메라의 파라미터를 활용해서 이동시킨 후에 intrinsic parameter matrix를 사용하여 2차원 점이 만들어집니다. 그렇게 했을 때의 차이의 제곱을 최소화시키는 방향으로 Rotation과 Translation을 구하는 것이 Motion only BA입니다.
- {R, t} : 최적화된 R, t
- fx, fy : focal length
- Cx, Cy : principal point
- p : robust Hubor cost function
- Xi : ith 3D point
- ㅠm, ㅠs : projection function (m : mococular, s : stereo)
Local BA
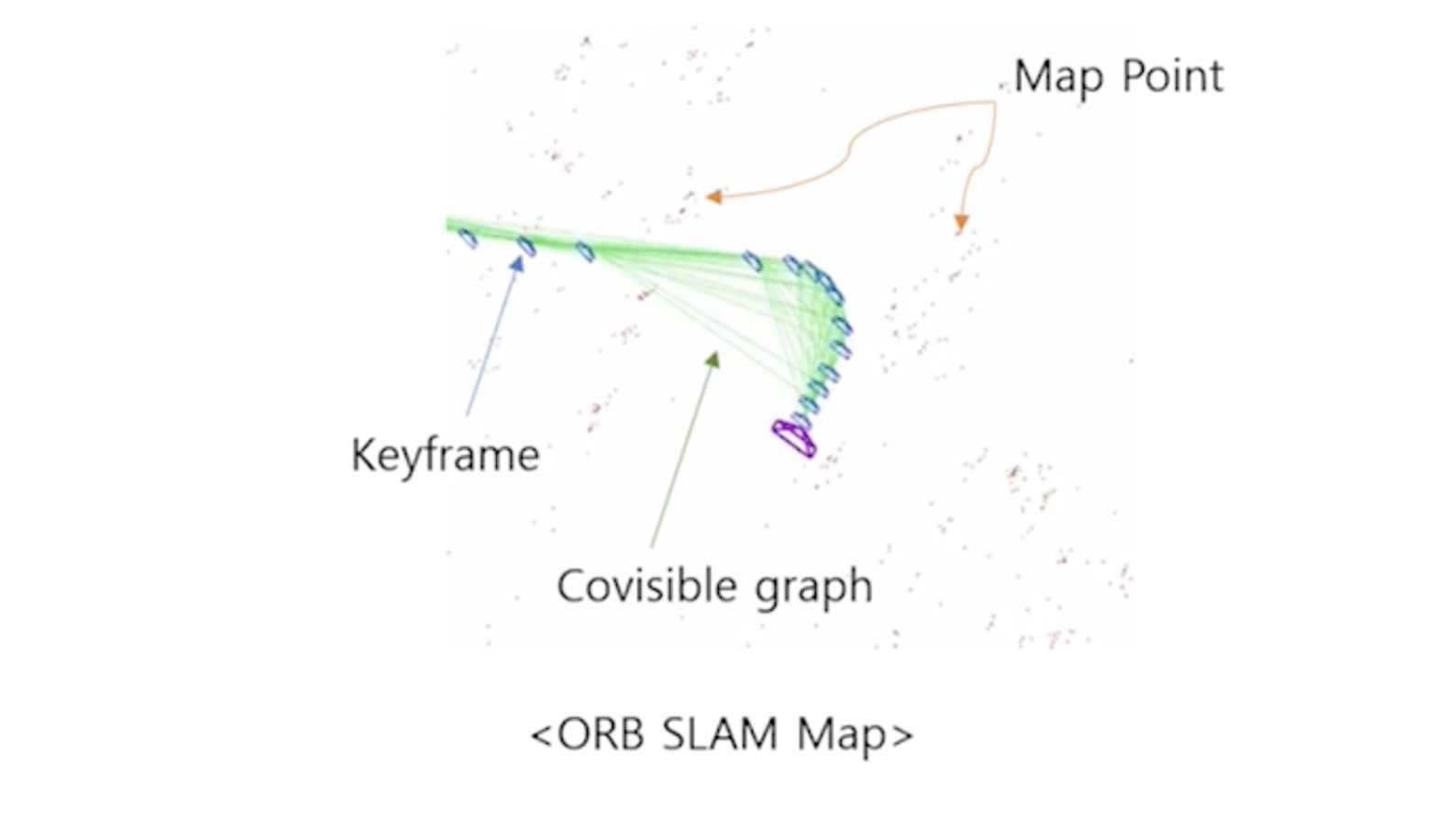

여러개의 카메라에 대해서 위치를 보정해줍니다. 즉, 각각의 키프레임이 촬영된 카메라의 위치를 보정해줍니다.
관측된 2차원 점과 각각의 카메라 위치로 이동시키고 투영시켰을 때의 에러를 최소화시키는 방향으로 Optimization합니다.
Full BA
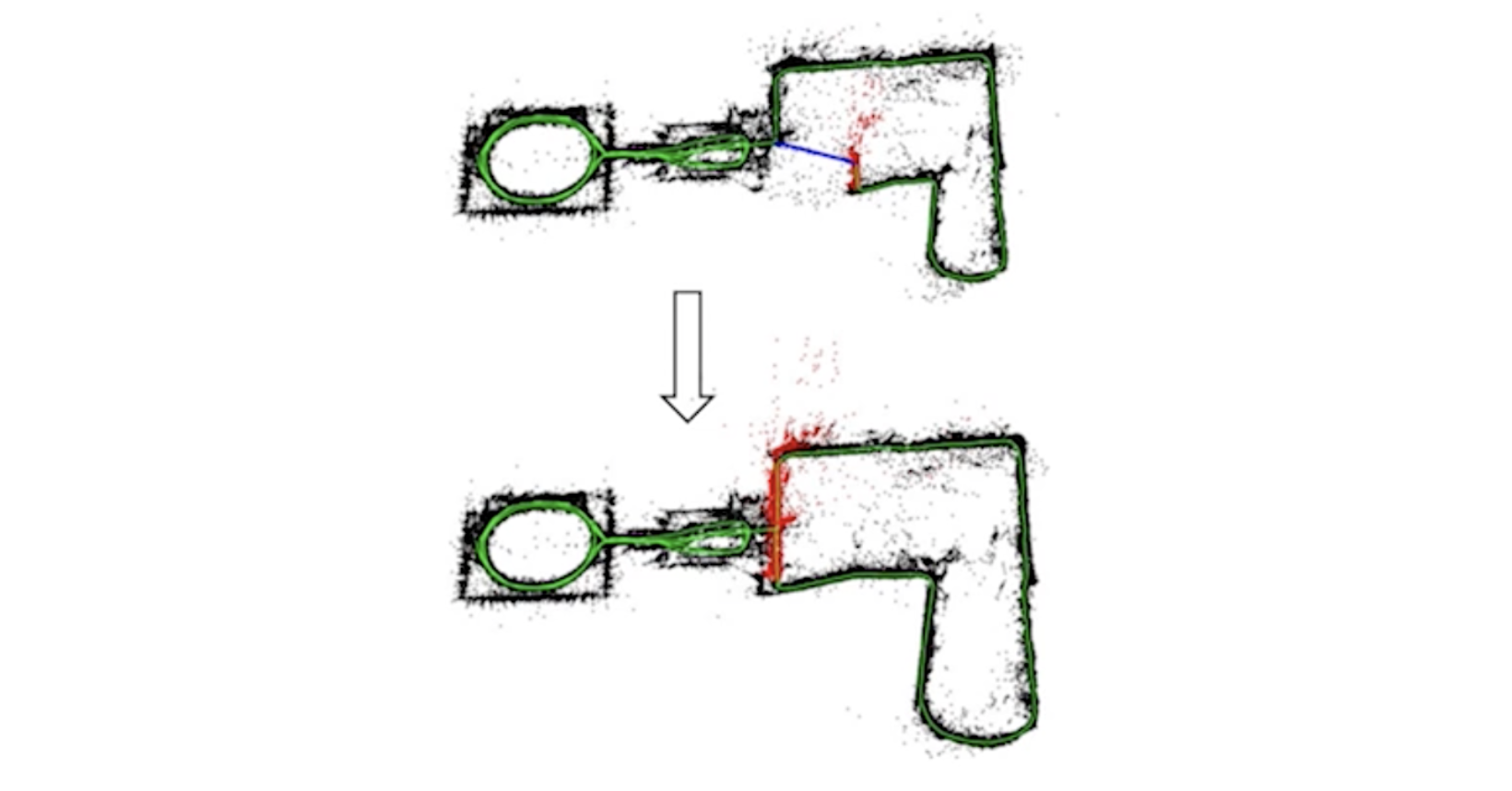
Full BA는 모든 키프레임을 활용한다고 생각하시면 됩니다. 수식은 Local BA 식에서 모든 키프레임과 포인트로 확장시킨다고 생각하시면 됩니다.
Abstract
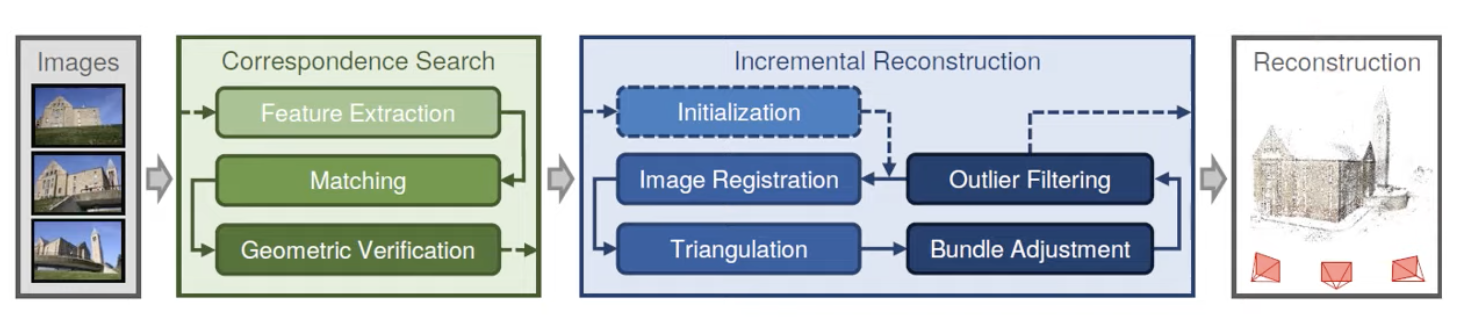
지금까지 내용을 요약하자면 다음과 같습니다.
첫번째, 먼저 input image가 들어오게 되면 Feature를 추출하기 위해 SIFT를 사용합니다.
두번째, Feature Matching을 시켜줍니다.
세번째, Epipolar Geometry를 이용해 각 이미지간의 Feature를 correspondence 시켜줍니다.
그 후, Incremental Reconstruction 박스에 들어가 이미지 데이터가 들어가게 되면 Triangulation인 삼각법을 통해 3D 좌표를 추종해 줍니다.
그리고 Bundle Adjustment와 Outlier Filtering 기법을 통해 에러를 줄입니다.
이러한 기법을 새로운 이미지가 들어올 때마다 반복하며 카메라의 위치와 3D 좌표를 최종적으로 추정합니다.
Ref.
2. https://cmsc426.github.io/sfm/#featmatch
.
'🖼 Computer Vision > 3D Reconstruction' 카테고리의 다른 글
| NeRF training pipeline (1) | 2022.09.14 |
|---|---|
| Multi-View Geometry (0) | 2022.08.13 |
| SFM(Structure from Motion) 구현 (with Python) (2) | 2022.08.12 |
| RANSAC (RANdom SAmple Consensus) (0) | 2022.07.28 |
| SIFT (Scale Invariant Feature Transform) (0) | 2022.07.28 |