
📌 이 글은 권철민님의 딥러닝 CNN 완벽 가이드를 바탕으로 정리한 내용입니다.
목차
- Backpropagation : 출력층부터 역순으로 Gradient를 전달하여 전체 Layer의 가중치를 업데이트하는 방식
- 미분과 편미분?
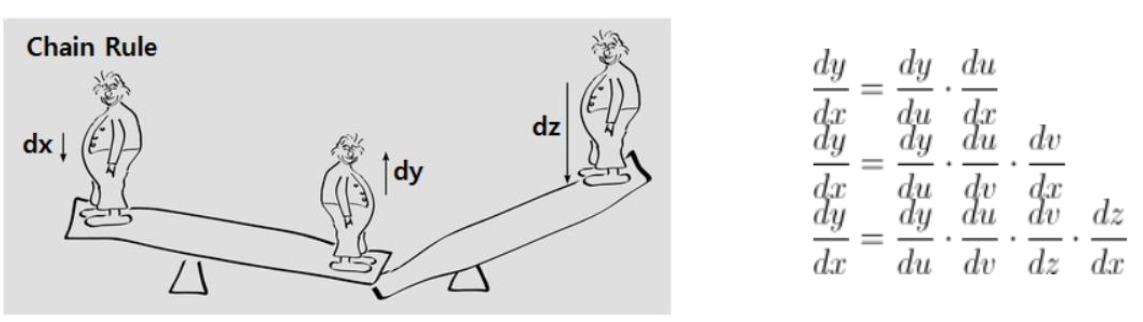
- Chain Rule (미분의 연쇄법칙)
- Chain Rule은 양파를 까는 것과 같다.
- Loss function의 편미분
- 의존 변수들의 순차적인 변화율
- Chain Rule의 의의
Backpropagation
출력층부터 역순으로 Gradient를 전달하여 전체 Layer 의 가중치를 업데이트 하는 방식
미분과 편미분?
일반적인 미분을 생각해보자.

편미분은 뭐였더라?
편미분은 여러 변수에 대한 식이 있을 때, 다른 변수는 고정시켜 놓고 하나의 변수에 대해서 미분하는 것이었다.

Chain Rule (미분의 연쇄 법칙)
이제 Chain Rule이 뭔지 알아보자. 알아보는 이유는 복잡한 DNN 안에서 Gradient를 어떻게 업데이트 하는지 알기 위해서이다.

이렇게 보니 그냥 합성함수를 미분하는 것이었다.
Chain Rule은 양파를 까는 것과 같다.

바깥 함수를 미분하고 다시 안쪽 함수를 미분하고,
바깥 함수를 미분하고 다시 안쪽 함수를 미분하고,
바깥 함수를 미분하고 다시 안쪽 함수를 미분하고,
...
양파를 오지게 까는 것이다.
Loss function의 편미분
퍼셉트론의 오차를 줄이기 위해 Loss function을 최소화 해야 하는데, 우리는 Loss function 안의 weight를 각각 다른 변수를 두고 편미분을 할 것이다.
Loss function에 대한 식을 다시 봐보자.

위의 Loss function에서 z = yi - (w0 + w1*xi) 로 표현할 경우 Loss function을 아래와 같이 간단하게 표현할 수 있다.
그리고 w1에 대해, w0에 대해 편미분할 수 있다.
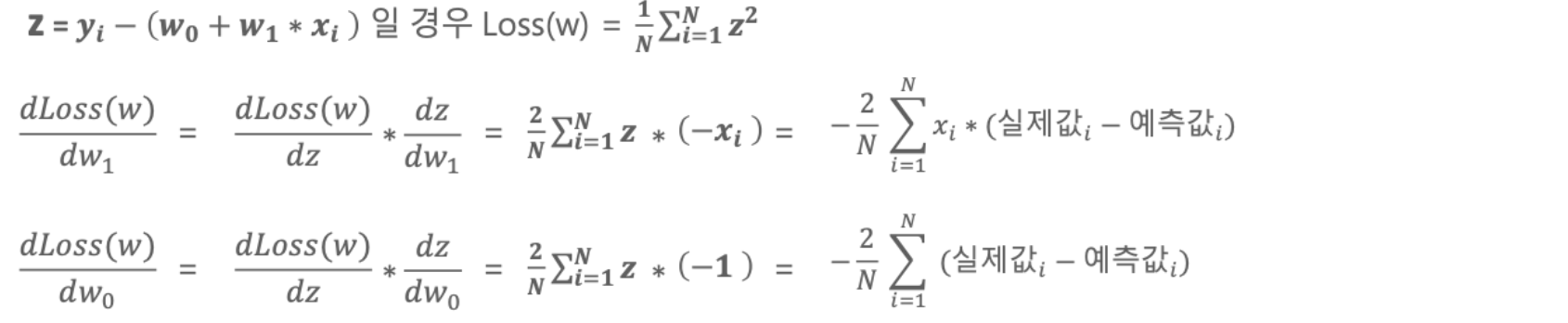
의존 변수들의 순차적인 변화율

위에서 본 것처럼 안쪽에 있는 것을 다른 것으로 대체하면 훨씬 더 쉽게 미분이 된다.
다른 것으로 대체하면 훨씬 더 쉽게 미분이 된다.
Chain Rule은 변수가 여러 개일 때, 어떤 변수에 대한 다른 변수의 변화율을 알아내기 위해 사용되는 특징이 있다.
변수y가 변수u에 의존하고,
다시 변수u가 변수x에 의존한다고 하면,
x에 대한 y의 변화율은 u에 대한 y의 변화율과 x에 대한 u을 변화율을 곱하여 계산할 수 있다.
Chain Rule의 의의
아무리 변수가 다양하게 구성된 함수의 미분이라도, 해당 함수가 미분 가능한 함수의 연속적인 결합으로 되어 있다면, 연쇄 법 칙으로 쉽게 미분이 가능하다 !
'🖼 Computer Vision > CNN' 카테고리의 다른 글
| CNN - Activation function (활성화 함수) (0) | 2022.01.20 |
|---|---|
| CNN - Backpropagation의 Gradient 적용 메커니즘 (0) | 2022.01.19 |
| CNN - Deep Neural Network (0) | 2022.01.19 |
| CNN - SGD, Mini-Batch GD (0) | 2022.01.19 |
| CNN - 보스턴 주택가격 Perceptron 기반 학습 (0) | 2022.01.14 |