

Optimization은 Loss를 최소화 하는 과정이다.
Loss가 최소가 되어야지만 좋은 prediction이 가능하다.

일반적으로 Gradient를 구하는 방법은 Numerical한 방법이다.
그러나 속도가 느리고 정확하지 않다.
따라서 해석적 방법인 Analytic 한 방법을 사용한다.
보통 gradient check를 할 때에는 Numerical gradient를 사용한다.

x에 가중치(W)를 곱하여 score값을 function에 넣으면 loss를 얻는다.
그리고 그것을 regularization loss와 더해주는 것을 total loss라고 한다.
이런 과정을 Computational graph라고 한다.

예를 들어서 하나하나의 모듈 별로 계산을 해나가는 방식을 학습해보자.
간단한 함수인 (x+y)*z 가 있고 x, y, z 값이 주어진다.

왼쪽에서 오른쪽으로 진행하는 것을 Forward Pass라고 한다.
input에 대한 gradient를 구하는 것이 학습의 목적이다.

이를 위해서 중간 매개변수인 q를 도입해본다.
q = x + y 로 구성된다.
f = q * z 로 구성된다.
우리가 원하는 것인 input 값에 대한 마지막 단의 영향력이기 때문에 df/dx, df/dy, df/dz를 구해야 한다.
그러기 위해서는 Backward Pass를 구해야 한다.

df/df 는 자기 자신에 대해 미분하기 때문에 1 이다.
녹색으로 표현된 값은 실제 값이고
빨간색으로 표현된 값은 gradient 값이다.

df/dz 는 q로 이미 구해 놓았다. q의 값은 3이다.
이때 q가 3이라는 의미는 z의 값을 h만큼 증가시키게 되면 f의 값은 3h 만큼 증가하게 된다는 의미이다.
즉 3배 만큼 영향력을 주고 있다는 의미이다.

df/dq 도 이미 z로 구해 놓았다. z는 -4이다.
q를 h만큼 증가 시킨다면 h는 4h 만큼 감소한다는 의미이다.

df/dy 는 구해놓지 않았다.
이때 사용해야 할 것이 Chain Rule 이다.
Chain Rule을 이용하면 df/dy는 -4가 된다.
y가 h만큼 증가할 때 f는 4h만큼 감소한다는 의미이다.

dq/dy 는 df/dy를 구하려는 직접적인 gradient 이기 때문에 local gradient라고 하고
df/dq 는 global gradient 라고 한다.

마찬가지로 x의 f에 대한 영향력은 -4이다.
x의 q에 대한 영향력은 1이다.

Local gradient는 Forward Pass 하는 과정에서 구할 수 있고 이것을 메모리에 저장해 놓는다.
Global gradient는 Backward Pass 하는 동안에 구할 수 있다.
즉 Backward Pass 시에 최종적으로 Chaining이 일어난다.
계속 Backward Pass를 함으로써 Gradient를 구하는 것을 Back propagation 이라고 한다.

각각의 input에 대한 최종적인 영향력을 구해보자.

맨 처음 gradient는 당연히 1이다.
df/df는 identity function이므로 위의 예제와 마찬가지로 1로 시작한다.

편미분으로 수식으로 적어
임의로 앞부분을 da 라고 표현하고 끝부분을 dL이라고 표현한다면 dL/da 을 구하는 것이 된다.
여기에 Chain rule을 위해 b를 도입하면, da/db 가 local gradient, dL/db 는 global gradient 가 된다.
1.37 기준에서 global gradient는 1이다.
그리고 1/x 이므로 local gradient는 -1/x^2 이 된다.
x = 1.37이기 때문에 1/(-1.37)^2 을 한 것이 local gradient가 된다.

따라서 -0.53 의 값을 얻게 된다.

0.37 기준에서 global gradient는 -0.53이다.
local gradient는 1이므로
1 x (-0.53) = -0.53 이다.
이런식으로 계속 구해준다.


-1.00 기준에서 global gradient는 -0.53 이고
local gradient는 e^x 값인 e^-1 이므로
-0.20이 된다.





이렇게 Backward Pass를 통해서 Input 5개에 대한 gradient를 모두 구할 수 있다.

여기서 다른 특성을 확인할 수 있다.
시그모이드에 대한 값이다.
파란색 네모 쳐진 부분을 sigmoid gate라고 할 수 있고, 위에서는 하나하나 다 계산하였지만 그럴 필요가 없다는 것을 보여준다.

시그모이드를 미분한 값이다.

이것을 다시 써보면 (1-sigmoid(x)) × sigmoid(x) 로 나타낼 수 있다.
즉 다른 어떤 값과의 연계가 없이 자기 자신의 표현이 되는 것이다.
그렇기 때문에 sigmoid gate에서는 아래와 같이 값을 손쉽게 얻을 수도 있다.

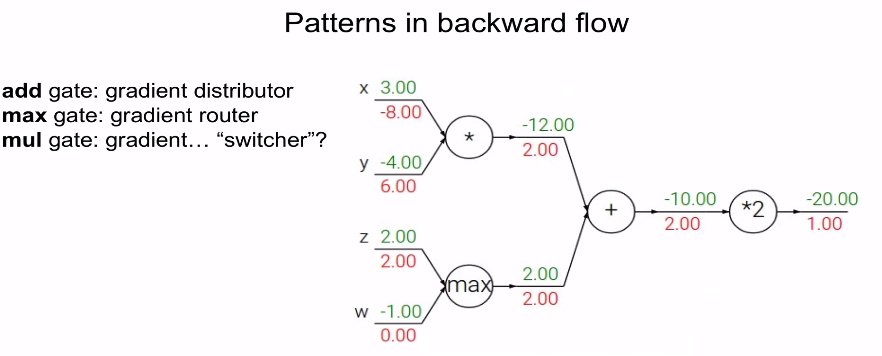
여기서 gradient의 특성을 알 수 있다.
Add gate는 local gradient가 1이다.
그래서 global gradient × local gradient 를 하면 local이 1이기 때문에 global gradient가 그대로 나오게 된다.
즉 Add gate는 gradient를 그대로 전해주는 역할을 하게 된다.
그래서 gradient distributor 라고도 불린다.
Max gate는 큰 값에게 gradient를 그래도 전하고 작은 값은 그냥 0으로 만들어서 보내버린다.
그래서 gradient router 라고도 불린다.
Mul gate는 맨 위에서 설명한대로 서로의 값을 교환한다.
따라서 gradient switcher라고도 불린다.

그런데 gradient가 하나의 값이 아니라 여러개면 어떻게 될까?
뒷 단이 여러개로 분기되는 상태인 경우에 여러개의 gradient를 그냥 더해주면 된다.
'🖼 Computer Vision > CNN' 카테고리의 다른 글
| CNN - 보스턴 주택가격 Perceptron 기반 학습 (0) | 2022.01.14 |
|---|---|
| CNN - Gradient Descent (0) | 2022.01.14 |
| CNN - Regression, RSS, MSE (0) | 2022.01.14 |
| CNN - Perceptron (0) | 2022.01.14 |
| Tensor 에 대한 이해 (0) | 2021.06.09 |