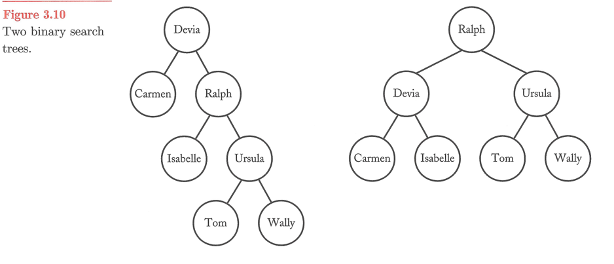

트리들 중 어느 트리로 만들어야 좋을까?
key 를 search할 때 걸리는 시간을 적게 하고 싶다.
비교횟수를 최소화 하고 싶다.
각 key를 찾을 때까지 key comparison의 최솟값
각각의 key들을 search할 확률이 1/7 로 하지않고 비교한다.

여러개의 키로 이루어져 있다.
각 키를 search할 확률이 나와 있다.

1 >> key1 을 찾을 때까지 비교를 3번 하게 된다. 0.7 × 3 + 0.2 × 2 + 0,1 × 1
2 >> key2 을 찾을 때까지 비교를 3번 하게 된다. 0.7 × 2 + 0.2 × 3 + 0,1 × 1
3 >> key3 을 찾을 때까지 비교를 3번 하게 된다. 0.7 × 2 + 0.2 × 1 + 0,1 × 2
4 >> key4 을 찾을 때까지 비교를 3번 하게 된다. 0.7 × 1 + 0.2 × 3 + 0,1 × 2
5 >> key5 을 찾을 때까지 비교를 3번 하게 된다. 0.7 × 1 + 0.2 × 2 + 0,1 × 3
5 번째 방법으로 찾는 것이 Optimal Binary Search 이다.

Pi : i번째 key를 탐색할 확률
Ci : i번째 key를 탐색할 때 key 비교의 횟수
Ci, Pi 곱의 합1을 최소화 시키는것이 목표이다.
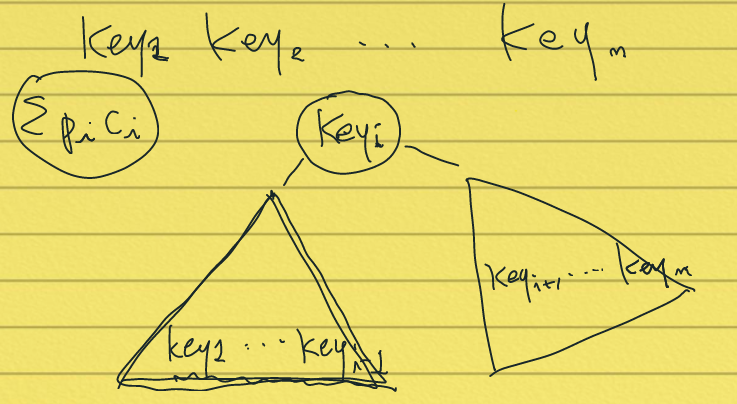
Root에 Key i번째를 넣는다는 전제하에 생각해보자
Left sub tree 에는 Key i보다 작은 것들이 들어간다.
Right sub tree 에는 Key i보다 큰 것들이 들어간다.
Left sub tree 자체로서 ∑PiCi 가 Optimal Binary Search Tree가 되어야 한다.
Right sub tree 자체로서 ∑PiCi 가 Optimal Binary Search Tree가 되어야 한다.


Key 1번 부터 n번 까지의 평균 비교 횟수를 A[1][n] 이라고 하자.
A[1][n] = minimum( A[1][k-1] + A[k+1][n] )
이 식에서 key K를 seach 할때의 횟수가 빠져있다.
=> ∑PiCi 에서 Ci가 1이므로 >> Pi이다.
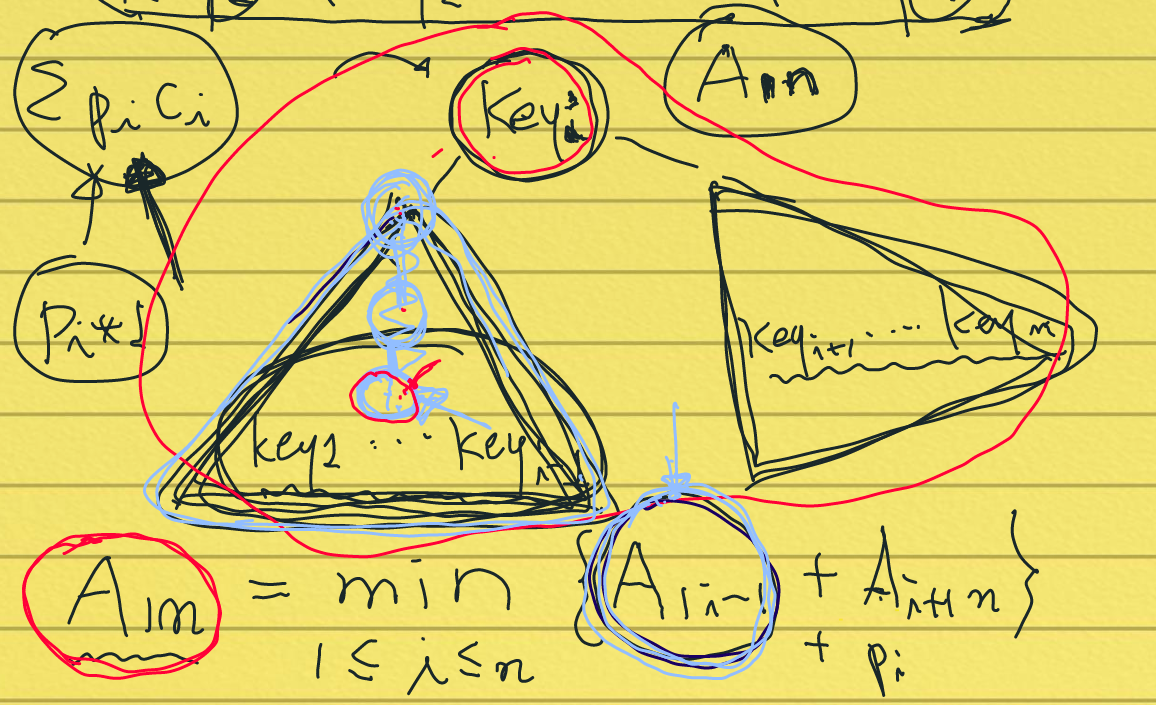
key 3을 찾는다면 하늘색 트리에서 3번 비교 + 빨간색 트리에서 4번 비교해야 한다.
확률값이 누적되므로 P1 + P2 +. .. + Pn 까지 더해줘야 하므로 결국엔 ∑Pk 이다.
A[1][n] = minimum( A[1][k-1] + A[k+1][n] ) + ∑Pk

A[i][i-1] 은 empty tree이다.
k가 i가 되는 경우가 발생하므로 A[i][i-1] =0, A[j+1][j] = 0 으로 정의해 줘야 한다.



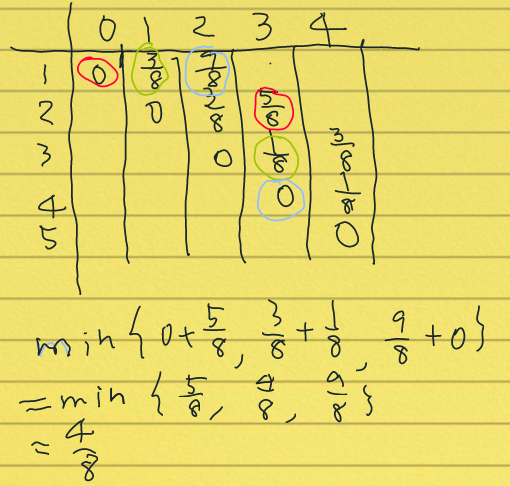
이게 끝이 아니라 P1 , P2, P3 를 더해줘야한다.



A[1]A[0] = 0
A[i][i] = p[i]
A[i]A[j] = minimum(i,j,k)
R[i][j] = k; // 최소가 되는 값을 R에 담아 놓는다.


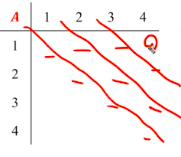
diagonal 계산하기

최적 값 R에 저장
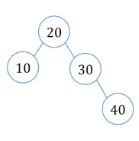
Optimal Binary Search Tree는 얘가 된다.
이진 탐색 트리의 특성
- 하나의 노드는 최대 두개까지의 자노드를 가질 수 있다.
- 부모 노드의 왼쪽 자식노드의 키 값은 부모 노드의 키 값보다 작다.
- 부모 노드의 오른쪽 자식 노드의 키 값은 부모 노드의 키 값보다 크다.
이진 탐색 트리의 예

이진 탐색 트리에서 어느 한 노드를 탐색하기 위한 최대 비교 횟수 : 그 트리의 깊이와 같음
이진 탐색 트리의 모든 노드가 각 한번씩 탐색된다고 가정할 때 총 비교 횟수
트리 (a) : 총 17번의 비교
트리 (b) : 총 19번의 비교
최적 이진 탐색트리 문제
: 트리의 각 노드가 탐색될 확률이 주어질 때, 그 트리의 평균 비교횟수가 최소인 탐색 트리를 구축하는 것이 목적이다.
이진 탐색트리를 구성하는 n개의 노드가 각각 K1, K2, ... , Kn의 key 값을 갖는다고 가정
key 값 Ki가 탐색될 확률 : Pi
key 값 Ki를 찾는데 필요한 비교 횟수 : Ci
이때 이진 탐색트리의 평균 비교 횟수 = ∑CiPi
이 값을 최소화 하는 이진 탐색 트리를 구성하는 것이 목표이다.
예제 : 노드가 3개인 모든 가능한 이진 탐색트리

여기서 key 값과 확률을 다음과 같이 정한다.
K1 = 1, K2 = 2, K3 = 3
P1 = 0.5, P2 = 0.3, Pe = 0.2

그러므로 (c) 와 (e)로 구성된 이진트리가 탐색시간이 가장 짧다.
다음 그림이 최적 해를 보여준다고 가정

이진트리의 평균 탐색 시간을 구하는 수식

동적 프로그래밍 기법을 적용하기 위해서 순환 방정식으로 표현하면

이때 Ti,i-1 = 0 으로 정의 (1 <= i <= n+1)
Ti,j 의 계산은 대각선 순서대로 한다.
예제 : 노드의 개수 n=4인 이진탐색트리의 각각의 키 값과 확률이 다음과 같다고 하자
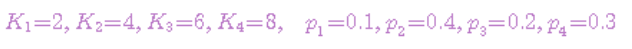
위에서 정의된 순환방정식에 의해서

위의 결과를 테이블로 나타내면 다음과 같다. 또한 최솟값을 갖는 k값을 테이블로 나타낼 수 있다.
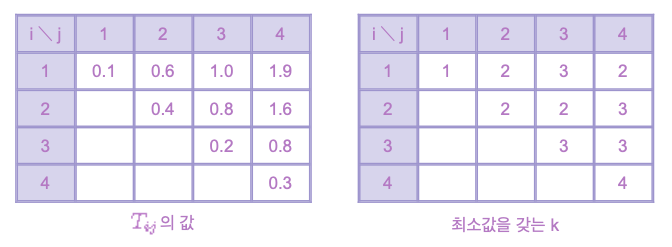
그러므로 최적 이진 탐색 트리는 아래와 같다.


'🕶 Algorithm > 알고리즘' 카테고리의 다른 글
| Traveling Salesperson Problem (TSP) - 0 (0) | 2020.05.13 |
|---|---|
| 알고리즘 과제 #3 (0) | 2020.05.12 |
| Binary Search Tree (0) | 2020.04.28 |
| Dynamic Programming - Chained Matrix Multiplication (0) | 2020.04.21 |
| Dynamic Programming - Floyd's Algorithm (0) | 2020.04.21 |