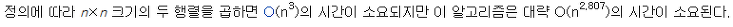
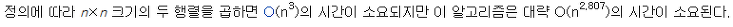
행렬의 곱셈
크기가 n x n인 두 행렬 A와B의 곱을 C로 나타내고자 한다.

의 원소를
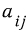
라 하고,

는 가로

는 세로를 나타낸다.
B와 C도 동일하게 표시한다.
행렬의 곱셈을 다음과 같이 표현할 수 있다.


C하나의 원소를 구하는데 드는 비용은,
곱셈

번과
덧셈
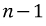
번이다.
따라서, C 전체를 구할 경우 C의 크기는 n x n 이므로
곱셈을
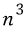
번
그리고 덧셈을

번하게 된다.
따라서, 두행렬을 구하는 복잡도는

이 된다.
알고리즘
A와 B를 체 F에 대한 정사각행렬이라고 하자. 두 행렬의 곱 C는 다음과 같다.

만약 A와 B가 2ⁿ × 2ⁿ 꼴의 크기가 아니라면 먼저 모자라는 행과 열을 0으로 채운다.
이 경우 행렬 곱셈이 끝난 뒤 행렬에서 필요한 부분만 다시 잘라 내야 한다.
이제 A, B, C를 같은 크기의 정사각행렬 네 개로 나눈다.

이 때,

따라서 다음이 성립한다.




이 과정에서는 필요한 연산의 수가 줄어 들지 않는다. 여전히 Ci, j 행렬을 계산하려면 여덟 번의 곱셈과 네 번의 덧셈이 필요하다.
이제 다음과 같은 행렬을 정의한다.







이 Mk 행렬들은 Ci,j 행렬을 표현하는 데 쓰이는데, 이 행렬들을 계산하는 데는 일곱 번의 곱셈(각 변수마다 한 번씩)과 10번의 덧셈이 필요하다. 이제 Ci,j 행렬은 다음과 같이 표현할 수 있다.




이 과정에서는 곱셈이 사용되지 않기 때문에, 전체 곱셈을 일곱 번의 곱셈과 18번의 덧셈(8+10)으로 처리할 수 있다. 큰 행렬에 대해서는 행렬의 곱셈이 덧셈보다 더 많은 시간을 필요로 하기 때문에 덧셈을 더 하는 대신 곱셈을 덜 하는 것이 전체적으로 더 효율적이다.
이 과정을 재귀적으로 반복할 경우 총

번의 연산이 필요하다.

실제로는 n이 작을 경우 정의에 따라 행렬 곱셈을 하는 경우가 빠를 수도 있기 때문에, 보통 작은 n에 대해서는 일반적인 방법으로 곱셈을 하도록 구현한다.슈트라센 알고리즘은 속도에 비해 수치 안정성이 떨어지는 것으로 알려져 있다.
두 행렬 A와 B를 곱한 결과를 C라 할 때, 실제 오차인

는

보다 작음이 알려져 있다. 이는 일반적인 행렬 곱셈보다 더 큰 오차이다.
스트라센의 경우 행렬의 곱셉을 하기 위해서는 정사각행렬에 대해서만 처리가 가능하다. 그렇지 않을 경우에는 행렬을 정사각 행렬로 변경하는 작업이 필요하다. 또한, 특정 단계에서는 행렬의 곱이 더 빠른 구간이 있으며 스트라센 행렬에서는 최적의 행렬 크기에서는 일반곱으로 행렬을 풀어나가는 방법이 있다. 스트라센 알고리즘에서 또 눈여겨 볼 부분은 연산으로 사용하는 M행렬을 구하는 부분에서도 행렬의 곱이 쓰인다는 점이다. 행렬의 곱은 스트라센으로 풀어나가는 알고리즘이기 때문에 M1을 예로 들면 M1 := (A + A) strassen (A + B) 이런식으로 풀어 쓸수 있다. 결국에는 재귀적인 호출을 통해 스트라센을 구해 나가는 방식을 이용하는 알고리즘인것 이다. 분할 정복알고리즘과 동일하며, M에서는 각 행렬을 작은 단위로 분할하며 최종 C행렬을 구하기 위해서는 분할된 원소를 재조립하는 과정으로 최종 행렬을 얻어낼 수 있다.


'🕶 Algorithm > 알고리즘' 카테고리의 다른 글
| Determining Thresholds (0) | 2020.04.19 |
|---|---|
| Multiplication of Large Integers (아주 큰 정수의 곱셈) (0) | 2020.04.18 |
| Divide-and-Conquer (part5) (0) | 2020.04.08 |
| Divide-and-Conquer (part4) (0) | 2020.04.02 |
| Divide-and-Conquer (part3) (0) | 2020.04.02 |