NeRF training pipeline
NeRF training pipeline
NeRF의 학습 과정에 대해서 알아보자. 논문에서 소개하는 method와 철학을 이해하는 것과 실제로 코드를 돌려보는 것과 학습 과정을 아는 것은 정말 차이가 크게 느껴져서 따로 정리하게 되었다.

각각의 Ray 상의 Radiance로부터 weighted sum된 RGB와 density 값을 가지고 Volume Rendering을 거쳐서 얻은 각각의 pixel 값을 구해야 한다. 그리고 그 pixel값과 Ground Truth의 RGB와의 MSE Loss를 Backpropagation 함으로써 Loss를 줄여가는 방향으로 MLP를 학습한다.
Create Ray origin, direction
input = (height, width, focal, pose), output = (ray origin, ray direction)

코드를 보면 NeRF의 input은 n개의 이미지와 그에 해당되는 n개의 pose를 넣는다. pose를 이용해 Ray를 정의하고, Ray로부터 Radiance들의 density의 weighted sum과 color를 구하여, 이미지의 color와의 MSE loss를 구하기 위함이다.
이를 위해 먼저 각각의 Ray를 만들어야 한다.
Ray를 만들어주기 위해 사진의 크기(width × height)에 맞는 그리드를 만들어준다(np.meshgrid()로 만든다).
Ray의 origin과 direction을 설정해주기 위해서 intrinsic parameter(focal length), extrinsic parameter(pose)가 필요한데 이는 colmap으로 구한다.
intrinsic, extrinsic parameter 구하는 과정
먼저 feature matching point를 구한 후, 최대한 잘못된 feature matching을 걸러서(five point algorithm, RANSAC), epipolar constraint(p' × E × p)를 만족하는 Essential Matrix를 구하고, Essential Matrix를 SVD를 이용한 4가지 변환 후보를 구한 후, 조건에 맞는 Rotation Matrix(회전 변환 행렬)와 Translation Matrix(평행 이동 행렬)를 구한다. (SfM 참조)
focal length와 width, height로 normalized coordinate를 만들어주고,
pose로 camera direction을 설정해준 다음, 각각의 ray direction은 camera direction과 camera 원점과 각 그리드와의 점까지의 벡터 합으로 구할 수 있다.
이렇게 모든 이미지에 대한 ray origin과 ray direction을 구해주게 되면, 아래 그림처럼 월드 좌표계에서의 모든 view에 대한 ray origin과 ray direction을 알 수 있다.

Create 3D point (o + td) , Stratified sampling
input = (ray origin, ray direction), output = (o+td, t)
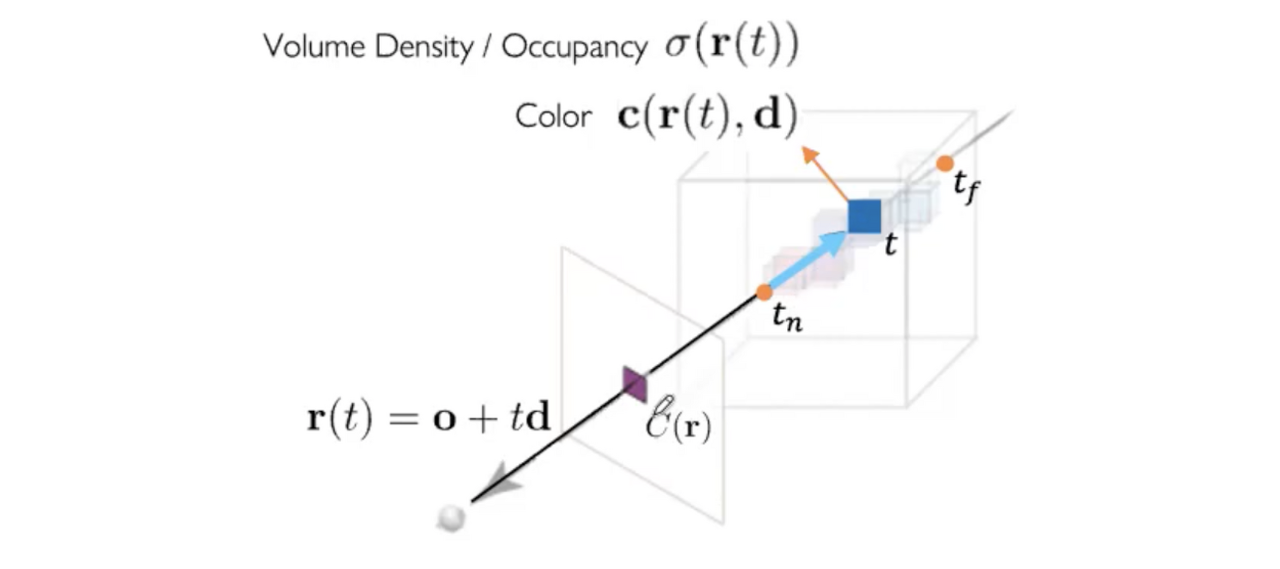
이제 각각의 Ray의 direction과 origin을 구했으므로, Ray 상의 Radiance들의 weighted sum을 구해야 한다. 그렇게 하기 위해서 Ray를 o + td 값의 형태로 만들고 t값에 대해 샘플링 해주어야 한다.
t 값을 설정하기 위해 ,먼저 near bound와 far bound를 설정하여 어디서부터 어디까지 샘플링할지 정한다. 즉, radiance field의 범위를 정하는 것이다. 그리고 Stratified sampling을 위한 segment의 갯수(n)로 near bound부터 far bound까지 나눈다. Stratified sampling을 하는 이유는 Ray를 등분해버리면 discrete 한, 일정한 데이터만 뽑아내게 돼서 한정된 점만 보기 때문에 continuous 하지 못한 모델이 되기 때문이다. 이것을 방지하기 위한 방법이다.
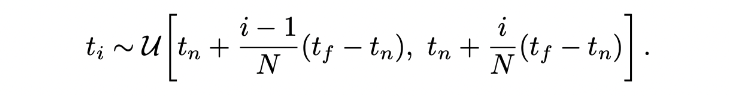
나눴으면 각 segment마다 uniform distribution으로 랜덤하게 noise 를 구하여 t 값(각 segment의 시작점)에 더해준다. t + noise
이렇게 t (각 segment 시작점 + noise)점을 설정하여 o + td 를 만든다.
Ray의 3D point들(radiance) 구현은 이러한 방식으로 이루어진다.
Compute Radiance Field
input = (NeRF MLP model, o+td sample points), output = (opacity, colors)
이제 이렇게 구현한 Ray의 각 point마다 transmittance와 volume density, 그리고 color를 구해주어야 한다.

위에서 구한 모든 Ray들을 MLP의 input으로 넣어준다.
MLP structure는 아래와 같다.

input으로 (x, y, z)를 Positional Encoding을 거쳐서 차원을 늘려준 다음 넣어준다. Positional Encoding을 하는 이유는 High frequency를 더 잘 표현하기 위함이다.
8개의 Layer를 통과한 다음 density를 뽑아내고 direction은 마지막에 넣어주는데, 그 이유는 Multi-view consistent 함을 위해서이다. 즉, direction에 따라 색깔이 변하면 안되기 때문에 direction을 제일 마지막에 넣고 한번만 layer를 통과한다. density는 보는 각도와 상관 없이 동일해야 하기 때문에 오로지 Coordinate 좌표만 가지고 추측할 수 있도록 제한한다.
이처럼 MLP를 거치면 density와 color가 나오게 된다.
Compute Adjacent Distances and Transmittance
input = (t, ray directions, opacity, interval distance), output = (density, transmittance)
하지만 여기서 나온 density는 transmittance가 고려되지 않은 density이다.
여기서 transmittance의 개념은, 위에서 설정한 near bound와 far bound 사이의 t 에서의 weight 값은, near로부터 t 까지의 density 값을 더한 값이 클수록, t에서의 weight가 작아진다는 개념이다.
그렇기 때문에 tn 에서 tf 까지 점들의 transmittance × density × color를 적분하여 Volume Rendering을 한다.
이를 위해 각 Ray 상의 sample(radiance)들의 transmittance를 포함한 density에 대한 weighted sum을 고려해야 한다.

코드에서는 두번째 식인 Optical models for direct volume rendering을 이용한다.
여기서 Ti (1 - exp(σi δi) 은 어떤 컬러가 Rendering 할 때, 2D 이미지의 컬러에 얼마만큼 contribution 할 수 있는지를 나타내는 Contribution weight라고 할 수 있다.
- Ti (1 - exp(σi δi ) : 얼마만큼 픽셀의 색깔에 contribution 하는가를 표현하는 weight
- Ti : t앞에 얼마만큼 물체를 가로막고 있는가
- (1 - exp(σi δi) : t에서 물체가 3차원에서 volume을 얼마나 차지하고 있는가
δi 는 sampling된 point들 간의 각각의 간격을 의미한다. δi = t_i+1 - t_i
sample들 간의 간격과 그에 따른 density를 고려하여, transimittance와 그 지점의 density에 대한 weighted sum을 구하게 되고, 이를 위에서 구한 color와 곱해주게 되면, 최종적으로 rendering 된 RGB 값을 구할 수 있게 된다.
이 weighted sum을 이용하여 각 ray의 rgb map, depth map과 disparity map도 구할 수 있다.
이렇게 구한 rgb map과 input image의 rgb의 MSE Loss를 Backpropagation 하면서 학습한다.