Paper Review - PlenOctrees


Background
Voxel : Volume과 Pixel의 합성어이며 직역하면 부피를 가진 픽셀이다. 즉, 픽셀을 3차원 공간으로 나타낸 것이다. 마인크래프트의 모든 물체가 Voxel로 이루어져 있다고 생각하면 된다. Voxel 자체는 명시적으로 인코딩된 위치를 갖지 않지만, 랜더링 할 때는 다른 Voxel의 위치에 대해서 해당 Voxel의 위치를 나타낸다. 큰 물체나 해상도가 올라갈수록 Voxel로 표현하기엔 연산량이 매우 많아진다는 단점이 있다.

Octree : 3D를 만드는데에 사용되는 tree 구조이다. 아래 그림처럼 각 노드는 8개(Octopus)의 자식노드가 있거나 아무것도 없거나 둘 중 하나이다. 각 자식 노드는 RGB 색상 정보를 가질 수 있다. 이런 구조는 트리 크기를 제한하기 때문에 메모리 효율이 좋다. 여기서 또 트리마다 필요 없는 부분을 가지치기를 하면 메모리를 더 축소할 수 있다.

Sparse 하다 : 2D 이미지 데이터가 정해진 격자에 pixel 값이 모두 존재하는 dense한 특성을 지녔다면, Point Cloud 데이터는 매우 sparse한 성질을 가지고 있다. 부연 설명을 하자면, 주어진 데이터의 3D 공간 안에는 Point들에 비해 빈공간이 상당이 많다는 것이다. 이러한 데이터는 크기에 비해 얻을 수 있는 유의미한 정보가 거의 없다. 이는 전처리 작업을 통해 Point Cloud 데이터를 정형화 데이터로 변환하여도 동일하게 가지고 있는 성질이다.

Sparse Voxel Octree : Octree의 데이터에 대해 Ray casting 하는 Rendering 기술이다. 장점은 해상도에 따라 세부적인 부분을 제안하면서 필요한 픽셀만 계산하면서 렌더링하고, 내부 Voxel을 3D 데이터셋에 포함시키지 않는다(표면 Voxel 만 포함). sparse는 '드문드문' 이라는 뜻을 가진다.
Introduction
기존의 NeRF 같은 Neural Rendering은 non-lambertian effect (view-dependent color change) 를 구현하고 상세하게 Rendering 하면서 storage 측면에서 장점이 있지만, 모든 샘플에 대해서 inference를 해야 하고, 이를 구현하기 위해서 모든 Viewing direction과 Spatial location에 대해서 Rendering view가 바뀔 때마다 MLP query 를 다시 행해야 하기 때문에 시간이 굉장히 오래 걸린다는 단점이 있다. 이 논문은 Spherical Harmonics를 통해 color를 factorization 함으로써 density와 color를 voxelize 하여 저장할 수 있게 하여 기존 NeRF 보다 3000배 이상 빠른 real-time rendering NeRF 기법을 제시한 연구이다. 이커머스 쪽의 웹 기술에 적합하다고 한다.
NeRF 등의 Neural Radiance Fields 를 이용하는 Neural Rendering 은 scene 에 대한 projected color 를 ray casting 방식으로써 계산한다. Discreatized 된 color 는 다음과 같이 쓸 수 있는데,

한 픽셀의 color estimation 을 위해서는, 번의 MLP query가 필요함을 알 수 있다. 만약 우리가 800x800 resolution으로 scene 을 Rendering 하기 위해서는, 800x800x192 (64 coarse and 192 fine : high frequency를 잘 표현하기 위한 2개의 network)이 필요하다. 이는 Neural Radiance Fields가 8 layer 의 shallow 한 MLP 임에도 불구하고 NeRF 의 real time rendering 을 어렵게 만드는 주요한 원인이다.

이러한 단점을 해결하기 위해, Memory-Inference Tradeoff 로써 미리 density 등의 값을 계산한 후 voxelize 하여 저장하는 방법 등을 생각해볼 수 있으나, NeRF 는 view-dependent 하게 color가 바뀌기 때문에 이를 미리 모두 계산하고 저장하는 것은 불가능하다.
이 논문에서 Sparse voxel-based octree를 통해 volume에서의 radiance를 모델링 하기 위한 appearance와 density를 저장한다. 그리고 non-lambertian effect를 구현하기 위해, voxel 위의 한 점의 RGB 를 Spherical Harmonics로 factorize 하는 방법을 통해 SH의 coefficient 만을 저장하여 octree 구조로 voxelized NeRF 를 caching 하는 방법을 제안한다.
다시 말하자면 RGB 값 대신 SH function의 coefficient를 생성하는 network를 학습하여, Octree의 잎에 그 예측값을 저장하도록 한다. 이런 방식으로 메모리 효율도 높이고 high quality로 나오게 한다. 그리고 이를 통해 150fps 수준의 rendering 속도를 달성하였다.
Method
NeRF의 voxelize의 가장 큰 장애물은 non-lambertian effect를 표방하는 NeRF의 color estimation 이다. view-dependent 하게 변하는 color를 표현하기 위해 original NeRF는 rendering viewpoint 가 바뀔 때마다 새로운 MLP inference 가 필요하고, voxel 의 한 점에서 가능한 모든 각도에 대한 color 를 저장하는 것은 불가능하기 때문에 NeRF 를 naive 하게 caching 하는 것은 challinging problem 이다.
논문에서는 Train된 NeRF를 PlenOctree로 변환할 수 있다고 한다. 이 Octree는 Spherical Harmonics coefficient를 저장하고 view-dependent radiance로 인코딩한다. 즉, PlenOctree를 통해 NeRF의 output 을 RGB 값이 아닌 Spherical Harmonics 의 각 coefficient 를 예측하도록 수정했다. 그러기 위해 View Direction의 입력이 필요 없는 NeRF의 변형인 NeRF-SH를 제시한다.
NeRF-SH

NeRF의 네트워크인 F에서 RGB 값이 아닌, SH coefficient k를 출력하도록 한다.

여기서 , 각 RGB 를 독립적으로 나누어서 SH factorization 으로 근사한다.
Spherical Harmonics(구면조화 함수)란 구면에 존재하는 주기 함수이다. Sphere 상에 존재하므로 2π를 주기로 주기가 정확히 일치해야 한다. Spherical Harmonics는 구면좌표계(3차원(r, θ, φ))에서 라플라스 방정식을 풀었을 때 얻을 수 있다. 다시 말해 Sphere 상에서 Laplacian Equation (Δf=0)을 만드는 function basis 들로, 각 SH 들이 독립적으로 특정 각도에 대한 scalar value를 embedding 하고 있다. Method의 의 SH visualization 에서 이를 확인할 수 있는데, SH basis 를 통한 factorization으로 non-lambertian color 를 표현할 수 있음을 알 수 있다. l은 서로 다른 기하 표현을 구분하는 값이고, m은 같은 기하 표현의 서로 다른 기저벡터를 구분하는 값이다.
이제 우리는 각 SH coefficient 값들을 통해 view-dependent color 를 다음과 같이 구할 수 있다.
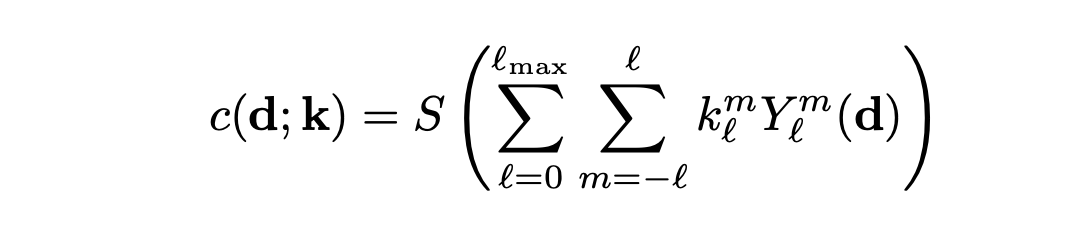
S = sigmoid function 으로 color를 normalize하고 SH basis로 view dependent하게 factorization 한다. 그렇게 되면 view direction을 input으로 넣어 주지 않고 conversion time에 view direction을 sampling 하지 않아도 된다. 그러면 arbitrary한 viewing angles에서 색깔을 효율적으로 query 할 수 있다.
이를 NeurIPS 2020 Neural Sparse Voxel Fields (NSVF) 관점에서도 생각해볼 수 있는데, PlenOctrees 와 비슷하게 NSVF 도 NeRF 를 voxelize 하여 저장하려고 하지만, 앞서 언급한 non-lambertian color estimation 을 위해 SH coefficient 가 아닌 32 dimension 의 feature vector 들을 각 voxel point 에 저장한다. 즉, NSVF 는 implicit 한 feature vector 로 이루어진 voxel grid 와 이에 대한 lightweight MLP 를 통해 fast rendering 을 구현했다.
PlenOctrees 는 이와 반대로 explicit 한 feature (i.e. coefficients of SH) 로 이루어진 voxel grid 와, explicit 한 spherical harmonic functions 을 통해 faster rendering 을 구현한 것이다. NSVF 와는 반대로 SH functions 들은 closed form 으로 알려져 있으므로 NSVF보다 (~1fps) 훨씬 빠른 Rendering (~150fps)이 가능하다.


SH function을 거치면 view direction이 SH basis 기반으로 표현될 수 있다.
Sprasity prior
Regularization 없이 unobserved region에 대해서 arbitrary geometry를 형성할 수 있다. image qaulity를 손상시키지는 않지만 conversion 할 때, 중요한 voxel space에서 안좋은 영향을 미칠 수 있다. 이 문제를 해결하기 위해서 NeRF training 중에 추가적인 Sparsity prior를 도입한다. 즉, 효율적인 voxel grid 의 구현을 위해서 저자들은 sparse 한 region 에 대한 surpass 역할을 하는 loss 를 추가하였다.

여기서 σk 는 K에서의 uniform한 density 값이며 λ는 하이퍼파리미터이다. 어떠한 particle의 density가 클 때에만 projected color에 기여하므로, 위 loss는 solid 하지 않은 particle들의 density 값을 0으로 만들어준다.

PlenOctree: Octree-based Radiance Fields

NeRF-SH을 training 하고 실시간 Rendering을 위해 Sparse octree 구조로 변환할 수 있다. PlenOctree는 view-dependent한 appearance를 모델링 하는 density와 SH coefficient를 저장한다.
Rendering
PlenOctree(Voxelized 된 NeRF-SH)의 rendering 과정은 매우 간단하다. 먼저 Ray-Voxel intersection을 구한다. (density와 color를 갖는 voxel boundary 사이의 segment sequence를 생성) 그 후 Original NeRF 와 같이 discreatized ray casting 을 계산한다. 실제 test 과정에서는, accumulated transmittance 값이 일정 threshold (0.01) 이하면 (즉, 굉장히 높은 확률로 빈 공간을 나타내는 ray) early stopping 하여 속도를 더욱 높였다고 한다.
Conversion from NeRF-SH
다음 세 과정을 거쳐서 voxelize 한다. 요약하면 solid 한 particle이 있는 voxel grid 만 남겨서 그 안에서 sampling을 통해 factorized 된 color를 저장하는 과정이다.
- Evaluation : density value 를 저장하는 uniformly spaced 3D voxel grid 를 구성한다.
- Filtering : threshold 보다 작은 density 값을 갖는 voxel은 제거한다. 즉 sparse voxel grid 를 구성
- Sampling : filtered voxel에 각 256 개의 random points를 sampling하여 coefficients of SH로 이루어진 vector 를 leaf node에 저장한다.
PlenOctree optimization
Volume rendering process가 fully differentiable 하기 때문에, original NeRF loss와 SGD를 통해서 octree를 directly optimize 할 수 있다고 한다. 이를 통해 일정 이상 NeRF가 학습된 이후로는 octree를 optimize 하는 것이 훨씬 빠르기 때문에 전체 pipeline의 converge를 original NeRF 대비 빠르게 끝낼 수 있다. 아래 실험에서 이를 확인할 수 있는데, NeRF 와 NeRF-SH 와 비교하여 훨씬 빠르게 학습되는 것을 알 수 있다.

Result

비슷한 방식을 사용하는 NSVF 대비해서도 rendering rate 가 100배 이상 차이가 난다.





voxelize 시켜서 저장하게 되면 확실히 NeRF 의 장점인 memeory efficiency 부분에서는 장점이 많이 퇴색되는 것이 보인다.
Ref.
PlenOctrees : https://alexyu.net/plenoctrees/
PlenOctrees 논문 : https://arxiv.org/pdf/2103.14024.pdf
.