Multi-View Geometry
Multi-View Geometry의 개념을 정리한 포스팅이다.
다크 프로그래머 님의 포스팅을 요약하였다.
목차
- 좌표계 (Coordinate System)
- 동차 좌표계 (Homogeneous Coordinates)
- 변환 (Transformation)
- 이미지 투영 (Image Geography)
- Epipolar Geometry
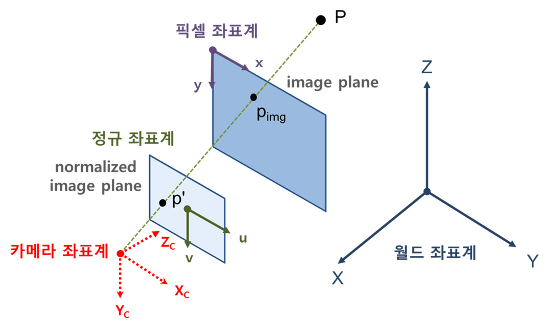
좌표계 (Coordinate System)
MVG에서는 크게 4가지 좌표계가 존재한다.
- 월드 좌표계 (World Coordinate System)
- 카메라 좌표계 (Camera Coordinate System)
- 픽셀 좌표계 (Pixel Image Coordinate System)
- 정규 좌표계 (Normalized Image Coordinate System)
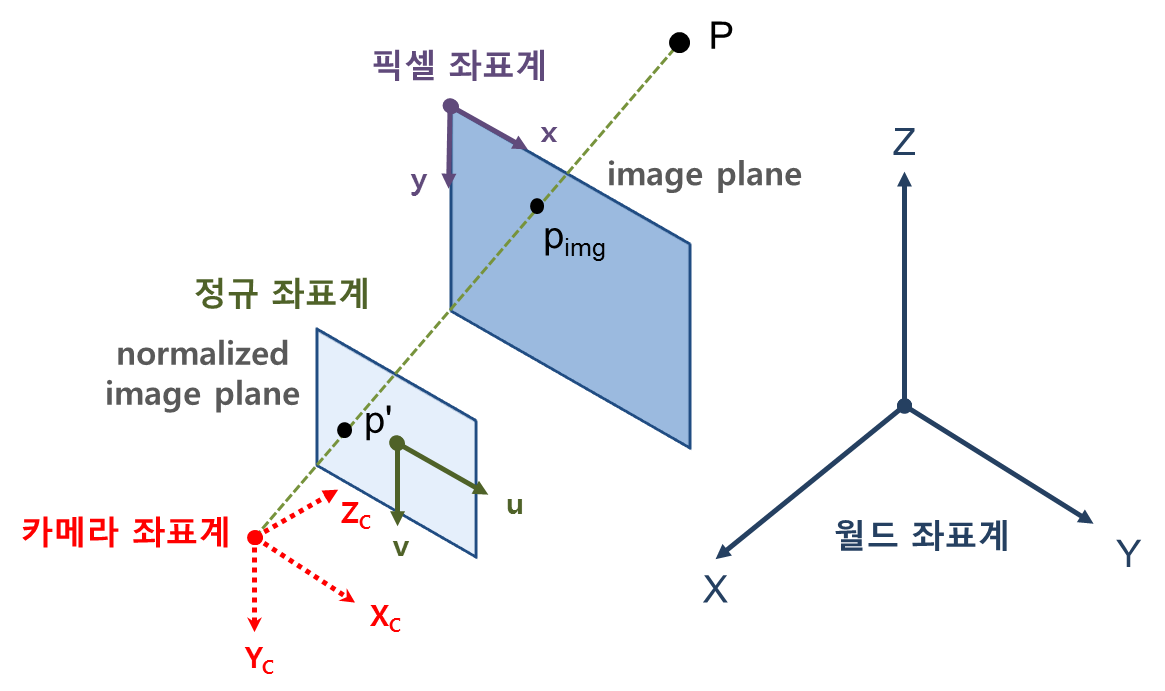
월드 좌표계 (World Coordinate System)
World Coordinate System 은 우리가 사물의 위치를 표현할 때 기준으로 삼는(우리가 살고 있는 공간의 한 지점을 기준으로 한) 좌표계이다. 즉, 물체를 볼 때 우리가 임의로 잡아서 사용할 수 있는 좌표계이다. 표기는 P = (X, Y, Z)로 표기한다. 단위도 임의로 설정해도 된다.
카메라 좌표계 (Camera Coordinate System)
Camera Coordinate System 은 카메라를 기준으로 한 좌표계이다. 아래 그림과 같이 카메라의 초점(렌즈의 중심)을 원점, 카메라의 정면 광학축 방향을 Z축, 카메라 아래쪽 방향을 Y축, 오른쪽 방향을 X축으로 잡는다. 단위는 World Coordinate와 동일해야 한다. 표기는 Pc = (Xc, Yc, Zc)로 표기한다.

픽셀 좌표계 (Pixel Image Coordinate System)
Pixel Image Coordinate System 는 우리가 실제 눈으로 보는 이미지에 대한 좌표계로서 아래 그림과 같이 이미지의 왼쪽상단(left-top) 모서리를 원점, 오른쪽 방향을 x축 증가방향, 아래쪽 방향을 y축 증가방향으로 한다.
영상좌표계(Image Coordinate System)라고도 불린다.
정규 좌표계 (Normalized Image Coordinate System)
Normalized Image Coordinate System 는 카메라의 내부 파라미터(intrinsic parameter)의 영향을 제거한 이미지 좌표계이다. 지금까지 나온 좌표계는 모두 매우 직관적인 좌표계이지만 정규 좌표계는 편의상 도입된 가상의 좌표계이다. 또한 정규 좌표계는 좌표계의 단위를 없앤(정규화된) 좌표계이며 카메라 초점과의 거리가 1인 가상의 이미지 평면을 정의하는 좌표계이다.
즉, 원래의 이미지 평면을 평행이동시켜서 카메라 초점과의 거리가 1인 지점으로 옮겨놓은 이미지 평면을 생각하면 된다.
원점은 광학축인 Zc와의 교점이며 Pixel Image Coordinate와 원점이 다르다. 표기는 p' = (u, v)로 표기한다.
Intrinsic parameter(K)를 알면 픽셀 좌표와 정규 좌표 사이의 변환이 가능하다.
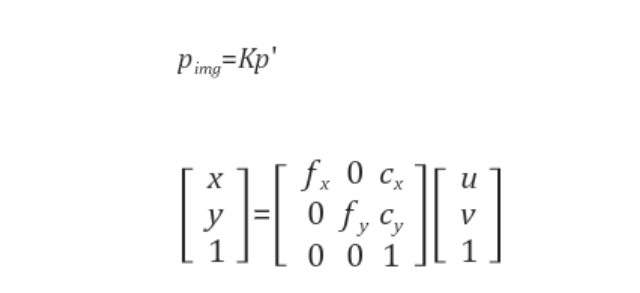
여기서 fx, fy는 초점거리(focal length), cx, cy는 주점(principal point, 광학축과 영상평면이 만나는 픽셀좌표)이다.
x = fx u + cx 이며 u = (x-cx) / fx 로 정리할 수 있다.
굳이 이렇게 정규 이미지 평면과 정규 좌표계를 도입한 이유는, 기하학적 해석을 위한 카메라간의 차이를 없애기 위함이다.
동차 좌표계 (Homogeneous Coordinates)
Homogeneous 좌표는 쉽게 말하면 (x, y)를 (x, y, 1)로 표현하는 것이다. 좀더 일반적으로 말하면 임의의 0이 아닌 상수 w에 대해 (x, y)를 (wx, wy, w)로 표현하는 것이다. 이렇게 표현하는 Homogeneous 좌표계에서는 스케일(scale)은 무시되며 (x, y)에 대한 Homogeneous 좌표 표현은 무한히 많이 존재할 수 있다. 원래의 좌표를 구하려면 끝 자리가 1이 되도록 scale을 바꾼 후 1을 없애면 된다.
Homogeneous 좌표계를 사용하면 affine 변환이나 perspective(projective) 변환을 하나의 단일(single) 행렬로 표현할 수 있다. 우리가 흔히 사용하는 Euclidean geometry 말고, Projective geometry에서 사용하는 좌표가 바로 Homogeneous 좌표계이다.
내가 공부하는 3D reconstruction에서 Homogeneous 좌표계가 중요한 이유는 3차원 공간의 물체를 사진으로 찍으면 이미지 평면에 투영(projection)되기 때문이다. 이미지 평면상의 한 점에 대한 Homogeneous 좌표라는 것은 이 점으로 투영되는 (ray 상의) 모든 점들을 한꺼번에 표현하는 방법이기 때문이 중요하다.
위에서 공부한 Normalized Image Coordinate System만 생각해도, 점 p'은 (u, v)로 표현되고 (u, v, 1)로 표현 되는데, Camera Coordinate로 봤을 때의 3D 좌표도 (u, v, 1)이다. 이 부분이 개쩌는거 같다.
사영 기하학(Projective geometry)
2차원 사영 기하학에서 두 homogeneous 좌표 (x, y, 1), (2x, 2y, 2)는 서로 같다. 왜냐하면 두 점 모두 동일한 한 점 (x, y)로 투영되기 때문이다.
유클리디언 기하학에서 익히 알고 있는 사실은 평행한 두 선(line)은 결코 만나지 않는다 이다. 그런데, 사영 기하학에서는 평행한 두 선의 교점을 구할 수 있다. 우리가 이미지에서 흔히 보는 vanishing point가 바로 그 교점이다.

사영기하학에서 직선의 방정식 ax + by + c = 0을 homogeneous 형태로 변환하면 ax + by + cw = 0이 된다. 여기서 ax + by + cw = 0은 직선 ax + by + c = 0 상의 점으로 투영되는 homogeneous 좌표 (x, y, w)들이 만족해야 하는 식을 나타낸다. 즉, ax + by + c = 0에 대응되는 homogeneous 좌표계 상에서의 방정식이다.
변환 (Transformation)
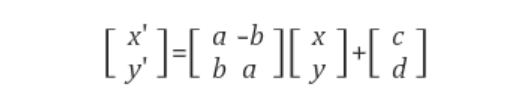
위의 식은 회전변환과 평행이동을 나타낸 행렬식이다. 평행이동(translation) 부분을 [tx, ty]라 쓰지 않고 [c, d]라 한 이유는 [c, d]가 물체의 평행이동량 뿐만 아니라 (영상원점을 중심으로 한) 회전변환으로 인한 이동량까지 같이 포함된 값이기 때문이다.
아래 그림의 탁구채의 평행 이동량에 대해서 생각해보자.
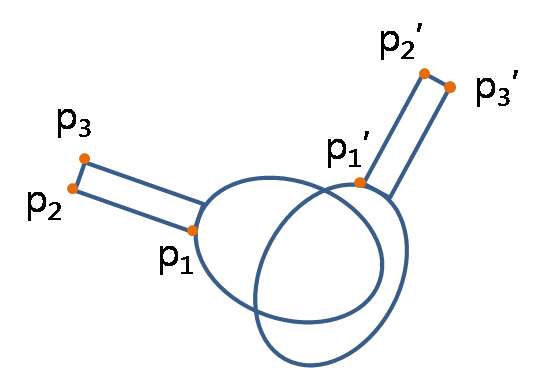
이건 절대적인 문제가 아니라, 기준의 문제임을 알 수 있다. 손잡이는 이동량이 크고 라바는 이동량이 작기 때문이다. 즉, 기준점을 정해야 평행이동량을 알 수 있다.
homogeneous 좌표 표현을 사용하면 회전, 평행이동 변환은 다음과 같이 하나의 행렬 변환으로 표현될 수 있다.
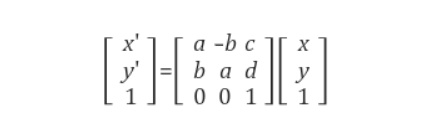
3D 변환에서도 homogeneous 좌표를 사용하면 다음과 같이 회전변환과 평행이동을 하나의 변환행렬로 즉, 선형변환 형태로 표현할 수 있다.
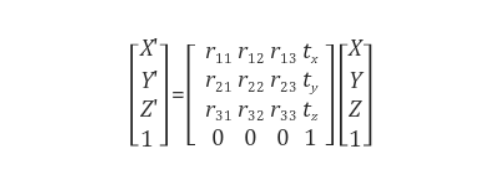
어떤 행렬 R이 회전변환이 되기 위한 필요충분조건은 RT = R-1, det(R) = 1 이라고 한다.
좌표축 변환
월드 좌표계 상에서 카메라 초점(카메라 좌표계의 원점)의 좌표를 (Fx, Fy, Fz), 월드 좌표계의 좌표축을 카메라 좌표계 좌표축으로 회전시키는 행렬을 R이라 하자.
이 때, 월드 좌표계의 점 (X, Y, Z)을 카메라 좌표계로 봤을 때의 좌표 (Xc, Yc, Zc)는 다음과 같이 구해진다.
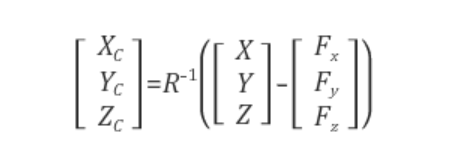
이미지 투영 (Image Geography)
3D 월드좌표에서 2D 픽셀좌표로의 변환 관계, 즉 이미지가 형성되는 과정을 정리해보자.
월드 좌표계 : P (X, Y, Z)
-> 카메라 좌표계 : Pc (Xc, Yc, Zc)
-> 정규 좌표계 : p' (u, z)
원근 투영 변환 (Perspective Projection Transformation)
Perspective projection은 3차원 공간의 점을 이미지 평면에 투영시키는 것이다.
위의 그림처럼 투영 기준점(projection reference point)을 원점으로 잡은 경우, 3차원 상의 점 P(X, Y, Z)를 p'(u, v)으로 투영시키는 변환 행렬은 아래와 같다.
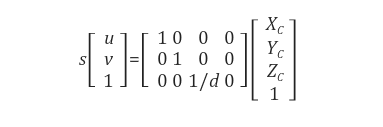
즉, 투영 평면이 Zc = d일 경우 (Xc, Yc, Zc, 1)는 (Xc, Yc, Zc/d) = (d*Xc/Zc, d*Yc/Zc, 1)로 투영된다.
위의 행렬에서 s 는 homogeneous 좌표 표현의 scale factor로서 점 P의 depth에 해당한다.
이미지 투영 모델
월드 좌표계 상의 한 점 (X, Y, Z)를 이미지 평면(픽셀 좌표계) 상의 점 (x, y)로 변환시키는 행렬을 H라 하면,
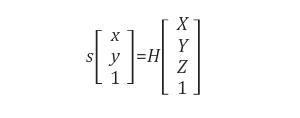
위와 같이 표현할 수 있다. 이 때, H는 3 x 4 행렬로서 아래와 같이 분해하여 표현할 수 있다.
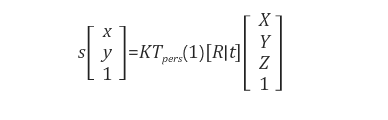
(x, y) = [K] x [Tpers(1)] x [R|t] x (X, Y, Z)
[R|t] 는 월드 좌표계를 카메라 좌표계로 바꾸는 변환 행렬,
Tpers(1)는 카메라 좌표계의 3D 좌표를 정규 좌표계(normalized image plane)에 투영시키는 프로젝션(projection) 행렬,
K는 카메라 내부(intrinsic) 파라미터 행렬로 정규 이미지 좌표를 픽셀 좌표로 바꾸어 준다.
Tpers(1)은 d = 1 즉, Zc = 1인 평면으로의 투영변환을 말한다 (즉, normalized image plane으로의 투영)
[R|t] :월드 좌표계 P (X, Y, Z) -> 카메라 좌표계 Pc (Xc, Yc, Zc)
Tpers(1) : 카메라 좌표계 Pc (Xc, Yc, Zc) -> 정규 좌표계 p' (u, z)
K : 정규 좌표계 p' (u, z) -> 픽셀 좌표계 pimg (x, y)
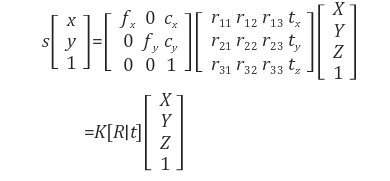
투영변환 Tpers(1)과 rigid 변환 [R|t]를 하나로 합치면 위와 같이 좀더 간단한 표현식이 된다.
- K : 내부 카메라 행렬(intrinsic camera matrix)이며, 카메라 내부 파라미터 (intrinsic parameter)를 나타낸다.
- [R|t] : 카메라 외부 파라미터 (extrinsic parameter)를 나타낸다.
- s : homogeneous 좌표표현의 scale factor로서 점 (X, Y, Z)의 depth에 해당한다.
Epipolar Geometry
Epipolar geometry는 동일한 사물을 서로 다른 두 지점에서 봤을 때, 이미지 A와 이미지 B의 매칭되는 쌍들 사이의 기하학적 관계를 다루는 것이다.
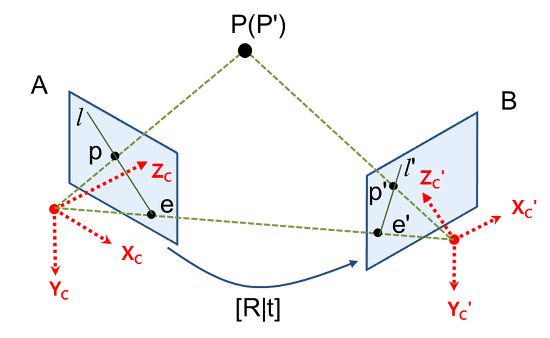
P를 카메라로 찍었을 때, 이미지 A에서는 p에 투영되고 이미지 B에서는 p'으로 투영된다고 하자.
그리고 두 카메라의 원점을 잇는 선과 이미지 평면이 만나는 점을 e, e'이라고 하고 이를 epipole이라고 부른다.
p와 epipole인 e를 잇는 직선 l, p'과 epipole인 e'을 잇는 직선 l'을 epipolar line 이라고 한다.
두 카메라 위치 사이의 기하학적 관계 [R|t]를 알고 있고, 이미지 A에서의 좌표 p를 알고 있을 때, 이미지 B에서의 p'을 구해보자. p에서 P까지의 거리(depth)를 모른다면 p로부터 3차원 좌표인 P를 복원할 수 없다. 그렇기 때문에 유일한 p'도 결정할 수 없다.
하지만 P는 카메라 A의 원점과 p를 잇는 직선(ray)상에 존재하기 때문에, 이 직선을 이미지 B에 투영시키면, 이 직선 위에 점 p'이 존재하는 것을 알 수 있다. 이 직선이 바로 epipolar line인 l' 이다.
정리하면, p로부터 유일한 p'을 결정할 수는 없지만 epipolar line인 l'은 유일하게 결정할 수 있다. 그리고 이러한 epipolar line을 계산해주는 변환 행렬이 Fundamental Matrix, Essential Matrix 이다.
Essential Matrix
3D 공간상의 한 점 P가 이미지 A에서는 p에 투영되고, 이미지 B에서는 p'에 투영됐다고 하면, 두 이미지 좌표 p와 p' 사이에는 어떤 관계를 만족하는 행렬이 항상 존재한다는 것이 epipolar geometry의 핵심이다. 여기서 p, p'은 normalized 이미지 평면에서의 homogeneous 좌표이다.
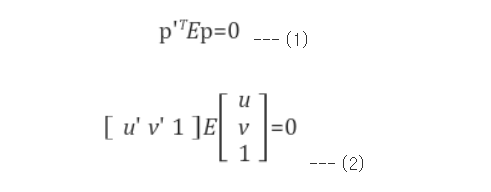
즉, 임의의 두 지점에서 찍은 이미지의 매칭점들은 항상 식 (1)을 통해 관계지을 수 있으며, 이 때 식 (1)을 epipolar constraint (또는 essential constraint), 이 3x3 행렬 E를 Essential Matrix라 부른다.
임의의 두 카메라 좌표축 사이의 관계는 회전, 평행이동에 의해 관계지을 수 있기 때문에 두 카메라 좌표축 사이의 3 x 3 회전행렬을 R, 3 x 1 평행이동 벡터를 t라 했을 때, 외부 공간상의 한 점을 두 카메라 좌표계에서 봤을 때의 관계를
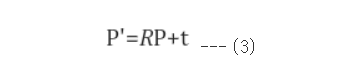
이렇게 나타낼 수 있다. 여기서 P는 A카메라 좌표계에서 봤을때의 3차원 좌표이고, P'은 B카메라 좌표계에서 봤을 때의 3차원 좌표이다.
이때 E를
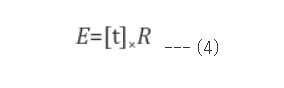
(4)와 같이 나타내면
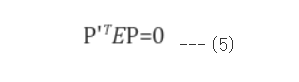
(5)가 만족됨을 알 수 있다.
(4)에서 [t]xR은 R로회전 시킨 다음에 t와의 외적으로 인한 변환을 뜻한다.
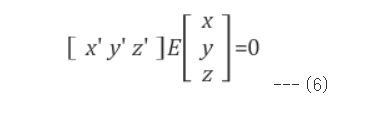
(5)의 E에 [t]xR 을 대입 해보면
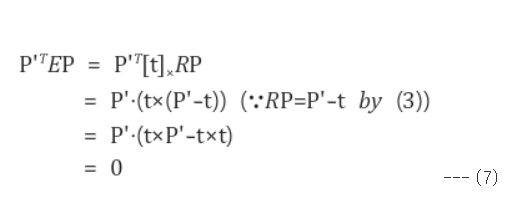
항상 0이 나오는 것을 확인할 수 있다.
Fundamental Matrix
Essential Matrix는 정규화된 이미지 평면에서의 매칭 쌍들의 기하학적 관계를 나타낸 행렬이며, 카메라 내부 파라미터인 K가 제거된 변환 관계이다. 반면 Fundamental Matrix는 카메라 내부 파라미터까지 포함한 두 이미지 평면의 픽셀 좌표 사이의 기하학적 관계를 표현하는 행렬이다.
두 이미지에 미칭되는 픽셀 좌표인 pimg, p'img 사이에는 항상

위의 식과 같은 관계를 만족하는 행렬 F가 존재하고 이를 Fundamental Matrix라 부른다.
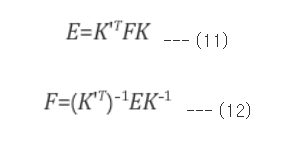
위의 식에서 A에 대한 카메라 내부 파라미터 행렬을 K, B에 대한 카메라 내부 파라미터 행렬을 K' 라 한다.
이미지 A, B 사이의 E는 위와 같은 식을 만족한다.
동일한 카메라로 촬영됐다면
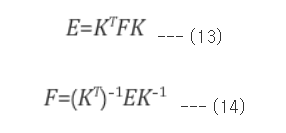
좀더 단순하게 표현된다.
추가로 이미지 픽셀 좌표 pimg와 normalized 좌표 p 사이에는 K에 대하여 아래와 같은 변환 관계를 가진다.

Epipolar constraint
위에서 Epipolar constraint는 두 이미지 평면 사이의 기하학적 관계에 따른 제약이라고 하였다.
SIFT 같은 방법으로 두 이미지와 대응되는 매칭 쌍을 알고 있을 때, 카메라 파라미터를 모른다면 F를 직접 구해야 한다. F를 구하기 위해선 최소 7쌍의 매칭점이 필요하다. 이 때 F의 scale까지는 알 수 없다. 왜냐면 공간 전체를 확대하거나 축소해도 동일한 이미지를 얻기 때문에 이미지만 가지고 스케일을 알 수 없기 때문이다.

카메라 파라미터 K를 알고 있다면 E만 구해도 된다. E를 결정하려면 5쌍이나 8쌍의 매칭점이 필요한데, 알고리즘에 따라 다르다. 이러한 알고리즘을 5-point algorithm 또는 8-point algorithm 이라고 한다. 구글 검색 ㄱㄱ
이렇게 Epipolar geometry에서 Essential Matrix를 알면 두 카메라 A, B 사이의 회전과 평행이동 관계를 파악할 수 있다.
opencv의 cv2.findEssentialmatrix()를 이용하면 input으로 SIFT의 결과물인 매칭점(p, p')들을 넣어서 Essential Matrix를 구할 수 있다. 그리고 cv2.recoverPose()를 이용하면 [R|t]도 구할 수 있다.
Triangulation
Triangulation은 두 이미지 평면 사이의 기하학적 관계인 E또는 F가 주어지고, 두 이미지 평면의 매칭 쌍 p, p'이 주어지면 이로부터 원래의 3D 공간 좌표 P를 결정할 수 있다는 것을 말한다. 즉, depth를 구할 때 하는 일이다.
Ref.
다크 프로그래머