SFM(Structure from Motion) 구현 (with Python)
Structure from Motion
Structure from Motion (SFM)
Structure from Motion Structure from Motion은 2차원 영상으로부터 3차원 정보를 추출하여 3D로 재구성하는(structure = 3D structure, motion=Camera pose) 것을 Structure from Motion(SFM)이라고 부릅니다..
woochan-autobiography.tistory.com
SfM 개념에 이어, Python 구현에 관한 포스팅입니다. 2 view만 구현하였고, 내용상 잘못된 부분이 있을 수 있으니 참고만 하시고 틀린 부분은 댓글로 지적해주시면 감사하겠습니다.
GitHub - SunWooChan/sfm
Contribute to SunWooChan/sfm development by creating an account on GitHub.
github.com
목차
- Google drive mount
- Load input images
- Extract features from image by SIFT
- Match features (find correspondence) between two images
- Estimate Essential matrix E with RANSAC
- Decompose essential matrix E to camera extrinsic[R|t]
- Generate 3D point by Linear triangulation methods
- Two view visualization
- Perspective 3 Point Algorithm
- Bundle Adjustment
Google drive mount
Colab 환경에서 진행하였습니다. 데이터는 누텔라 이미지를 이용하였고 구글 드라이브에서 마운트 했습니다.
# 구글 드라이브 마운트
from google.colab import drive
drive.mount('/content/drive')
!pwd
!ls
Load input images
먼저 opencv로 이미지를 가져옵니다.
import cv2
import sys
import numpy as np
from matplotlib import pyplot as plt
img1 = cv2.imread('/content/drive/MyDrive/Colab_Notebooks/GIST/nutellar2/nutella1.jpg')
img2 = cv2.imread('/content/drive/MyDrive/Colab_Notebooks/GIST/nutellar2/nutella2.jpg')
img1 = cv2.cvtColor(img1,cv2.COLOR_BGR2RGB)
img2 = cv2.cvtColor(img2,cv2.COLOR_BGR2RGB)Extract features from image by SIFT
이제 가져온 두개의 이미지에서 feature point를 얻기 위해서 opencv의 SIFT를 이용했습니다. SIFT는 크기, 회전, 조도, affine의 변화 및 noise에 불변하는 특징을 추출하는 알고리즘입니다. (자세한 설명은 SIFT 링크 참조) ORB나 다른 라이브러리도 존재하지만 ORB를 쓰면 좀더 정확하지만 keypoint가 적게 추출됩니다.
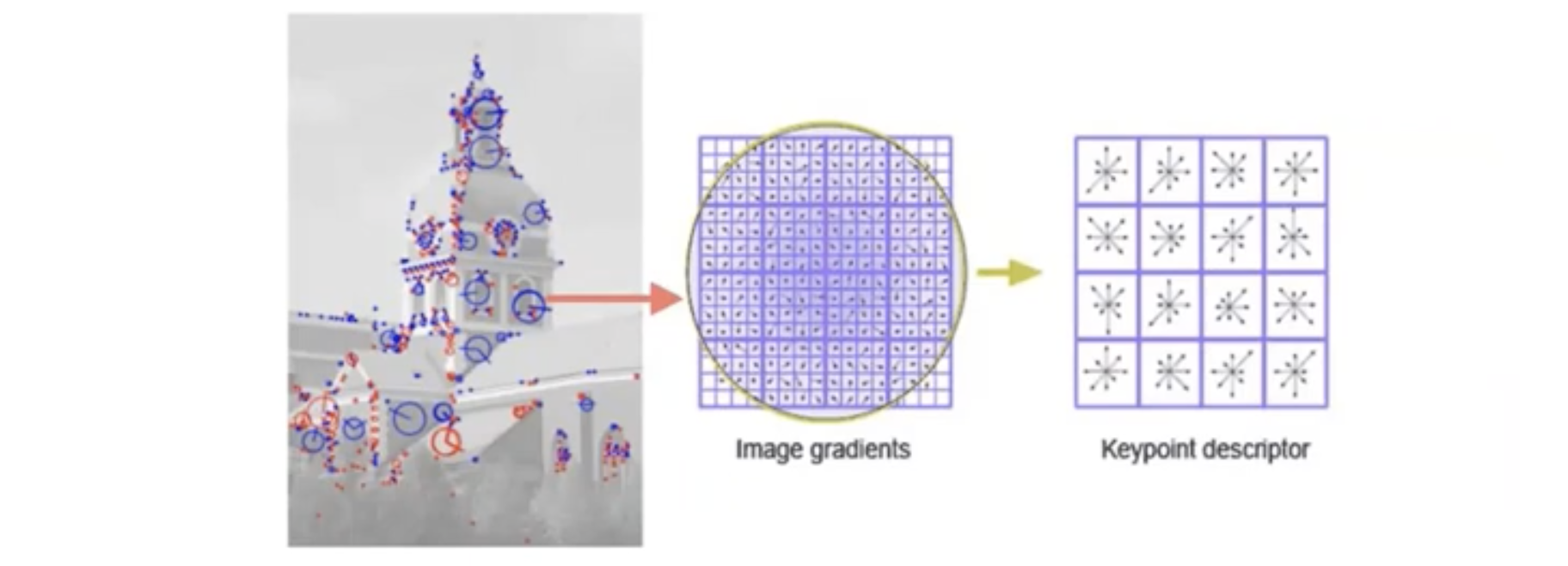
cv2.detectAndCompute() 로 해당 이미지의 key point와 descriptor를 저장합니다.
여기서 keypoint는 두 이미지간의 공통된 특징을 갖는 부분입니다.
그리고 descriptor는 keypoint를 포함하는 16 x 16칸의 정보를 의미하는데(keypoint의 지문이라고도 함), descriptor가 필요한 이유는, keypoint끼리 매칭을 하려면 하나의 keypoint 정보만으로는 매칭이 어렵기 때문입니다. 그렇기 때문에 keypoint를 기준점으로 설정하고 16 x 16칸의 정보를 이용해서 매칭할 수 있도록 지문을 남겨두는 것입니다. descriptor 안에는 window의 gradient 크기 및 방향의 정보가 들어있습니다.
sift = cv2.xfeatures2d.SIFT_create()
img1_kp, img1_des = sift.detectAndCompute(img1, None)
img2_kp, img2_des = sift.detectAndCompute(img2, None)
img1_draw = cv2.drawKeypoints(img1, img1_kp, None)
img2_draw = cv2.drawKeypoints(img2, img2_kp, None)
plt.figure(figsize=(20, 20))
plt.imshow(img1_draw)
plt.show()
print(len(img1_draw))
이미지 위에 키포인트를 그려보면 아래와 같이 그려지고, 각각 4528개와 5066개의 feature가 추출됩니다 .

Match features (find correspondence) between two images
이제 두 이미지 간에 keypoint를 매칭 시켜봅시다.
매칭을 위해서 cv2.BFMatcher()라는 메쏘드를 사용할건데, cv2.BFMatcher()는 가능한 모든 경우에 대해 다 계산해본 후 최적의 결과를 반환하는 알고리즘(Brute Force Algorithm)을 이용한 메쏘드입니다. cv2.BFMatcher( ) 함수는 image 1의 descriptor와 가장 유사도가 높은 image 2의 descriptor를 찾습니다. image 1의 모든 descriptor를 대상으로 거리를 모두 구한 다음에 가장 짧은 거리를 갖는 image B의 descriptor를 찾습니다.
이제 위에서 설명한대로 SIFT로부터 얻어낸 keypoint와 descriptor를 비교하면서 차이가 작은 keypoint와 descriptor 쌍이 매칭시켜봅시다. BFMatcher() 중 비슷한 쌍을 찾는 방법(NORM_L2, NORM_HAMMING)은 다양하지만, 그중에서 유클리드 거리를 이용한 knn 알고리즘을 이용했습니다. 유클리드 거리로 1차 매칭을 하고, 가까운 키의 비율을 통해 matching이 제대로 되었는지 확인합니다. (0.8 이상이 되면 그 key는 버립니다)
그후 cv2.drawMatches()를 이용하여 두개의 이미지와 연결된 keypoint를 이어줍니다.
# Brute force matching with k=2
bf = cv2.BFMatcher()
matches = bf.knnMatch(img1_des, img2_des, k=2)
# bf = cv2.BFMatcher(cv2.NORM_L2, crossCheck=True)
# matches = bf.match(img1_des, img2_des)
# Ratio test and retrieval of indices
matches_good = [m1 for m1, m2 in matches if m1.distance < 0.80*m2.distance]
sorted_matches = sorted(matches_good, key=lambda x: x.distance)
res = cv2.drawMatches(img1, img1_kp, img2, img2_kp, sorted_matches, img2, flags=2)
plt.figure(figsize=(20, 20))
plt.imshow(res)
plt.show()
print(len(sorted_matches))
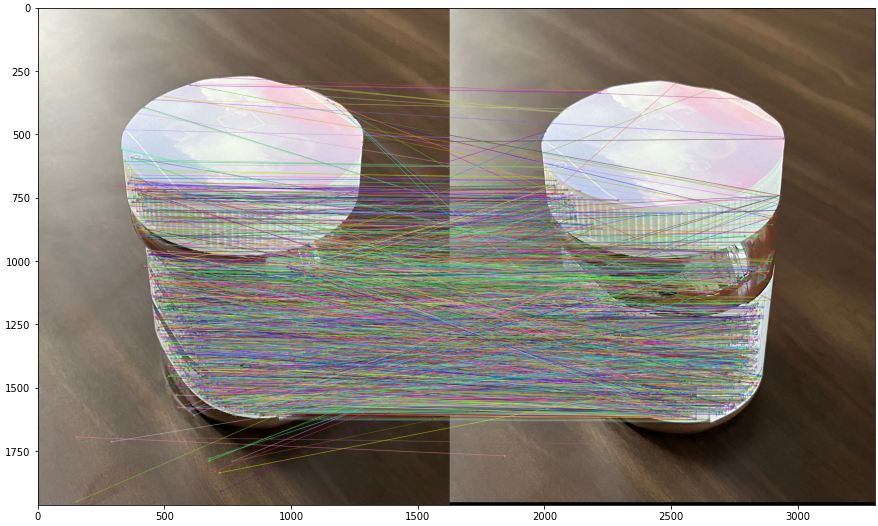
두 이미지의 keypoint를 잇고, 여러개의 feature 중에서 2965개의 feature가 매칭되었습니다. 그러나 매칭된 이미지를 보면 매칭된 부분이 대각선으로 이어지거나, 딱봐도 다른 부분이 매칭된 것을 볼 수 있습니다. 이제 이렇게 잘못 매칭된 부분을 처리해주어야 합니다.
Estimate Essential matrix E with RANSAC
잘못 매칭된 부분을 처리해주기 위해 왼쪽 이미지의 keypoint에서 오른쪽 이미지의 keypoint로의 변환행렬을 찾아야 합니다. 하지만 카메라와 누텔라와의 depth를 모르기 때문에, 왼쪽 이미지의 keypoint로부터 변환되어 유일하게 결정되는 오른쪽 이미지의 점을 구하진 못합니다.
하지만 왼쪽 이미지의 keypoint는, 왼쪽 카메라의 원점과 누텔라의 한 점을 잇는 직선(ray) 상에 존재하기 때문에, 이 직선을 오른쪽 이미지에 투영시키면 오른쪽 이미지의 keypoint가 이 투영된 직선 위에 있음은 알 수 있습니다. 이 투영된 직선이 바로 epipolar line 입니다. 그리고 그 epipolar line을 계산해주는 변환행렬이 바로 Essential Matrix 입니다.
그렇기 때문에 Essential matrix를 구해야 합니다. Essential Matrix를 다시 정리하면, 정규화된 이미지 좌표에서의 매칭 쌍들 사이의 기하하적 관계를 설명하는 행렬입니다. 카메라 내부 파라미터 행렬인 K가 제거된 좌표계에서의 변환 관계입니다.
왜 Essential Matrix를 구해야 하는지에 대한 자세한 설명
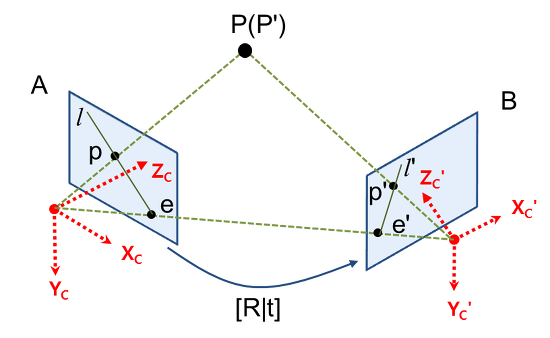
위 그림으로 예를 들자. 누텔라 통인 P를 카메라로 찍었을 때, P는 왼쪽 이미지 A에서 p에 투영되고 이미지 B에서는 p'으로 투영된다고 하자. 그리고 두 카메라의 원점을 잇는 선과 이미지 평면이 만나는 점을 e, e'이라고 하고 이를 epipole이라고 부른다. p와 epipole인 e를 잇는 직선 l, p'과 epipole인 e'을 잇는 직선 l'을 epipolar line 이라고 한다.
두 카메라 위치 사이의 기하학적 관계 [R|t]를 알고 있고, 이미지 A에서의 좌표 p를 알고 있을 때, 이미지 B에서의 p'을 구해보자. p에서 P까지의 거리(depth)를 모른다면 p로부터 3차원 좌표인 P를 복원할 수 없다. 그렇기 때문에 유일한 p'도 결정할 수 없다.
하지만 P는 카메라 A의 원점과 p를 잇는 직선(ray)상에 존재하기 때문에, 이 직선을 이미지 B에 투영시키면, 이 직선 위에 점 p'이 존재하는 것을 알 수 있다. 이 직선이 바로 epipolar line인 l' 이다.
정리하면, p로부터 유일한 p'을 결정할 수는 없지만 epipolar line인 l'은 유일하게 결정할 수 있다. 그리고 이러한 epipolar line을 계산해주는 변환 행렬이 Fundamental Matrix, Essential Matrix 이다. 그리고 epipolar constraint 인 p' x E x p = 0을 만족시키는, E를 Essential Matrix라고 한다. (만약 보정된 이미지를 사용하고 초점 거리에 의해 나눠진 지점을 정규하시키면 F와 E는 동일하다.)
요약하자면, 두 장의 사진으로 3D reconstruction을 하려면, 왼쪽 이미지의 keypoint를 변환했을 때, 오른쪽 이미지의 keypoint로 변환되는 모델을 찾기 위한 것이고, 그 모델이 바로 Essential Matrix이다.
Essential Matrix를 구하기 위해서 위의 잘못된 매칭 부분인 outlier를 걸러주어야 합니다. 이때 RANSAC을 이용합니다. RANSAC은 무작위로 샘플 데이터들을 뽑은 다음에 최대로 컨센서스가 형성된 모델을 선택하는 방법입니다.
그럼 왜 RANSAC을 이용할까요?
예를 들어, Least square method(최소 자승법)으로 아래와 같은 포물선을 모델링하면 outlier들로 인해 엉망이 되어버립니다.
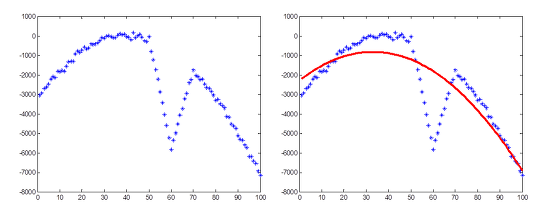
그러나 RANSAC 을 이용하면 아래와 같은 깨끗한 결과를 얻을 수 있습니다.

우리의 목표는 최적의 Essential Matrix를 구하는 것 입니다.
3D 좌표계의 한 점(P)은 왼쪽 이미지와 오른쪽 이미지의 각각의 epipolar line 위에 투영됩니다. 그러므로 왼쪽 이미지의 한 점 p를 오른쪽 이미지에서 찾기 위해서는 오른쪽 이미지의 epipolar line을 탐색하면 됩니다. 이때 만약 정확하게 매칭된다면, p' x E x p = 0 을 만족하는데 이것을 epipolar constraint라고 합니다. (여기서 p는 왼쪽 이미지의 한 점, p'은 오른쪽 이미지의 한 점 입니다.)
정상적이라면 최대한 epipolar constraint인 p' x E x p = 0 을 만족시켜야 합니다. 따라서 위에서 얻은 SIFT의 결과물인 왼쪽 이미지의 keypoint(p1)를 p로, 오른쪽 이미지의 keypoint(p2)를 p'으로 하고, p' x E x p = 0을 만족하는 Essential Matrix를 구하는 것 입니다.
다시 순서대로 정리하자면
- 왼쪽 이미지의 keypoint(p1)와 오른쪽 이미지의 keypoint(p2)를 input으로 넣어서,
- 이들 중 random하게(5-point) 뽑아내서 그에 맞는 Essential Matrix를 구하고, (5-point algorithm)
- p' x E x p = a 에서, a가 특정 threshold(0에 가까운) 보다 작은 것을 만족하는 가장 많은 수의 inlier를 갖는 최적의 모델인 Essential Matirx를 뽑아내면 됩니다.
Preprocessing
이를 수행하기 위해 먼저 각 이미지의 정규 좌표계를 전처리 하였습니다.
# queryIdx : 1번 이미지의 feature point index
# trainIdx : 2번 이미지의 feature point index
query_idx = [match.queryIdx for match in matches_good]
train_idx = [match.trainIdx for match in matches_good]
#Getting float based points from good matches
p1 = np.float32([img1_kp[ind].pt for ind in query_idx])
p2 = np.float32([img2_kp[ind].pt for ind in train_idx])
print(p1.shape)
print(p1[:3])
img1_pts = np.array([img1_kp[m.queryIdx].pt for m in matches_good]).reshape(-1, 1, 2).astype(np.float32) # 픽셀 좌표
img2_pts = np.array([img2_kp[m.trainIdx].pt for m in matches_good]).reshape(-1, 1, 2).astype(np.float32)
print(img1_pts.shape)
print(img1_pts[:3])결과는 아래와 같습니다.
(876, 2)
[[343.9091 506.02542]
[347.58115 799.80347]
[347.97467 957.2783 ]]
(876, 1, 2)
[[[343.9091 506.02542]]
[[347.58115 799.80347]]
[[347.97467 957.2783 ]]]
Code 1
E, mask = cv2.findEssentialMat(p1, p2, method=cv2.RANSAC, focal=3092.8, pp=(2016, 1512), maxIters = 500, threshold=1)cv2.findEssentialMat() 함수를 이용하면 한번에 최적의 E와 inlier를 output으로 얻을 수 있습니다. 파라미터로 RANSAC, RANSAC 반복 횟수와 threshold 등을 넣을 수 있습니다. focal length와 principal point는 colmap으로 구합니다.
findEssentialMat(): 두 이미지 사이의 essential matrix를 계산하여 반환. 입력할 내용은 5쌍 이상의 매칭 이미지 좌표쌍과 카메라 파라미터(초점거리, 주점). 내부적으로 5-point 알고리즘을 사용. 이미지 좌표로는 normalized 좌표가 아닌 픽셀 좌표를 입력
Code 2
하지만 저는 RANSAC을 구현하고 싶어서, cv2.findEssentialMat()이 가지고 있는 기능 중, Essential Matrix만 뽑는 기능인 5-point algorithm 만을 이용한 코드를 짜보려고 하였습니다. python에는 matlab의 ‘calibrated_fivepoint’ function이 없기 때문...
따라서 아래와 같이 코드를 구현해보았습니다. (결국 cv2.findEssentialMat()가 모든 것을 구현하고 있어서 제대로 작동이 안되는 코드입니다. 따라서 구현 과정만 참고하시기 바랍니다.)
def randomsample(p1, p2):
p1p2 = np.concatenate((p1, p2), axis=1)
p1p2_ = p1p2[np.random.randint(p1p2.shape[0], size=len(p1)), :]
p1s = p1p2_[:,:2]
p2s = p1p2_[:,2:]
return p1s, p2s
def RANSAC(p1, p2, iteration):
b_inlier = np.array([[]]) # best inlier
b_E = None # best Essential Matrix
tmp_inlier_len = 0 # tmp inlier의 개수
for i in range(iteration):
# choice random sample
p1s, p2s = randomsample(p1, p2)
# 5-point algorithm (with intrinsic parameter, epipolar constraint = 0, no RANSAC)
cur_E, cur_inlier = cv2.findEssentialMat(p1s, p2s, focal=3092.8, pp=(2016, 1512),
maxIters = 0, threshold=0.1)
# inlier 추출
inlier_idx = np.where(cur_inlier==1)
pts1 = np.vstack([p1[i] for i in inlier_idx[0]])
pts2 = np.vstack([p2[i] for i in inlier_idx[0]])
if cur_E is None:
continue
# inlier 수가 가장 많은 최적의 E 추출
if len(pts1) > tmp_inlier_len: # 현재 inlier 수 > 가장 많은 inlier 수
b_E = cur_E
b_inlier = cur_inlier
tmp_inlier_len = len(pts1)
return b_E
위의 SIFT로 얻은 두 이미지의 keypoint(p1과 p2)를 넣어서, random하게 뽑아내고, p' x E x p = 0를 만족하는, 가장 많은 inlier 수를 갖는 Essential Matrix를 반환합니다.
cv2.findEssentialMat()에는 epipolar constraint의 몇 이하로 Essential Matrix를 추출할 지의 threshold 파라미터, 어떤 알고리즘을 통해 five point를 고를 지에 대한 method 파라미터, 반복 횟수인 maxIters 파라미터, intrinsic parameter K인 focal(focal length)과 pp(principal point )파라미터가 있습니다.
intrinsic parameter에 관하여
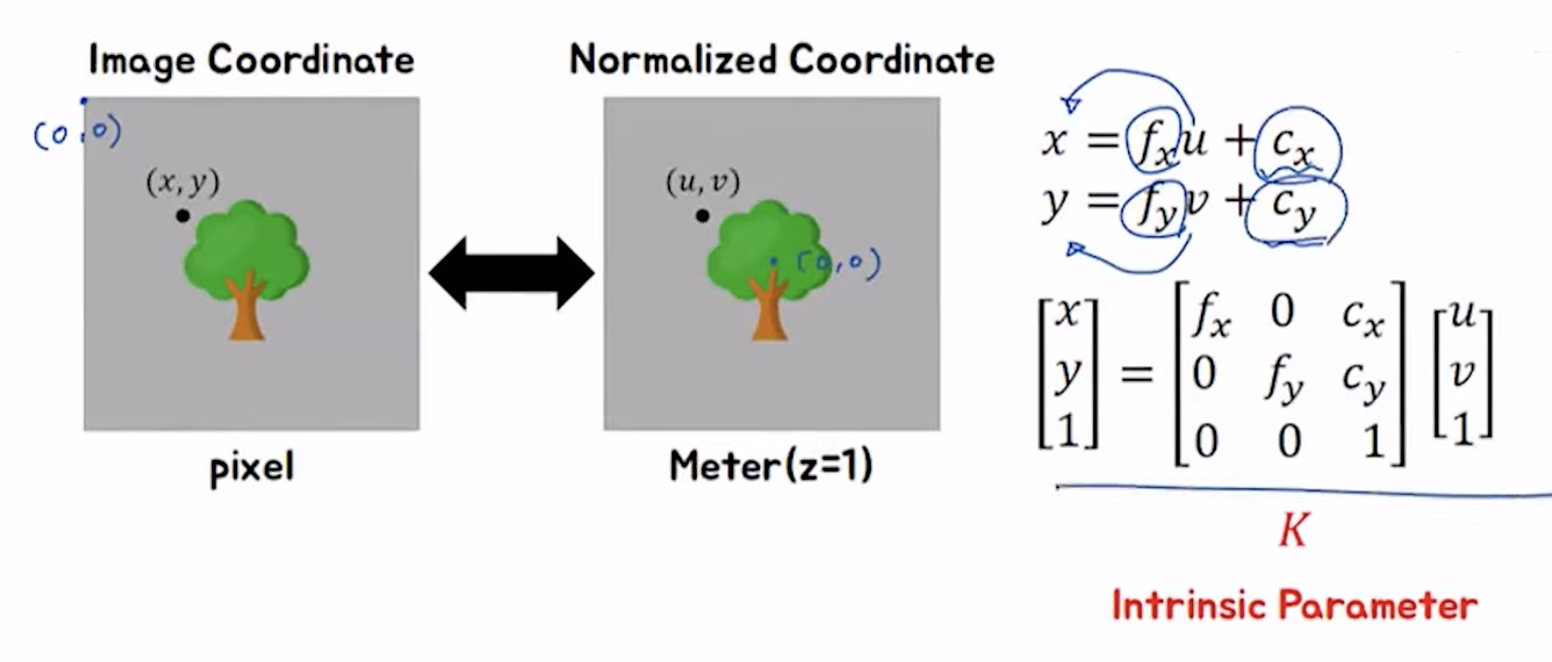
intrinsic camera matrix : K
1. fx, fy (focal length) : 렌즈 중심 <-> image sensor 과의 거리 (pixel 단위)
2. fx : 초점거리가 가로방향 cell 크기의 몇 배인지
3. fy : 초점거리가 가로방향 cell 크기의 몇 배인지
4. cx cy : 이미지에서 pixel 좌표는 좌상단 모서리를 원점으로 하기 때문에 최종 좌표는 principal point를 더한 값으로 나타냅니다.
Code 3
아래 코드는 오류 코드인데 matlab의 ‘calibrated_fivepoint’ function이 python에도 있다면 잘 작동했을 것 같은 코드입니다(저의 추측...). 여러 방면으로 시도해보면서 cv2.findEssentialMat() 의 파라미터를 아무리 바꿔봐도, 5-point algorithm 의 기능만 수행해서 Essential Matrix만 나오게끔 할 수가 없었습니다.
def RANSAC2(p1, p2, iter, threshold):
b_inlier = np.array([[]])
b_E = None
tmp_inlier_len = 0
for i in range(iter):
# 5개의 Random sample 추출
p1s, p2s = randomsample(p1, p2)
# 5-point algorithm
E, cur_inlier = cv2.findEssentialMat(p1s, p2s, maxIters = 0)
# inlier 추출
inlier_idx = np.where(cur_inlier==1)
pts1 = np.vstack([p1[i] for i in inlier_idx[0]])
pts2 = np.vstack([p2[i] for i in inlier_idx[0]])
# intrinsic parameter 설정
skew = 0.0215878
K = np.array([[3092.8, skew, 2016], [0, 3092.8, 1512], [0,0,1]])
K_inv = np.linalg.inv(K)
# (x,y) -> Homogeneous Coordinate (x,y,1) 로 변환
a, b = rescale_point(pts1, pts2, len(pts1))
if E is None:
continue
# Epipolar constraint = 0
cur_E = (b @ K_inv @ E @ K_inv.T @ a.T)
c = []
for i in range(len(pts1)):
c.append(cur_E[i][i])
c = np.array(c)
# inlier 수가 가장 많은 E 추출
tmp_inlier_len = len(c[(c<threshold) & (c>0)])
if len(pts1) > tmp_inlier_len: # 현재 inlier 수 > 최고 inlier 수
b_E = cur_E
b_inlier = cur_inlier
tmp_inlier_len = len(pts1)
return b_E각 이미지의 좌표의 Epipolar constraint(p' x E x p = 0)를 고려하기 위해 Homogeneous Coordinate (x, y, 1)로 바꿔주는 함수 rescale_point() 를 먼저 만들었습니다.
intrinsic parameter(K)까지 포함하여 epipolar constraint를 고려하면 아래와 같은 식을 만족해야 합니다.
아래 식에서 p, p'은 정규 좌표계의 좌표이고, pimg, pimg'는 픽셀 좌표계의 좌표입니다.
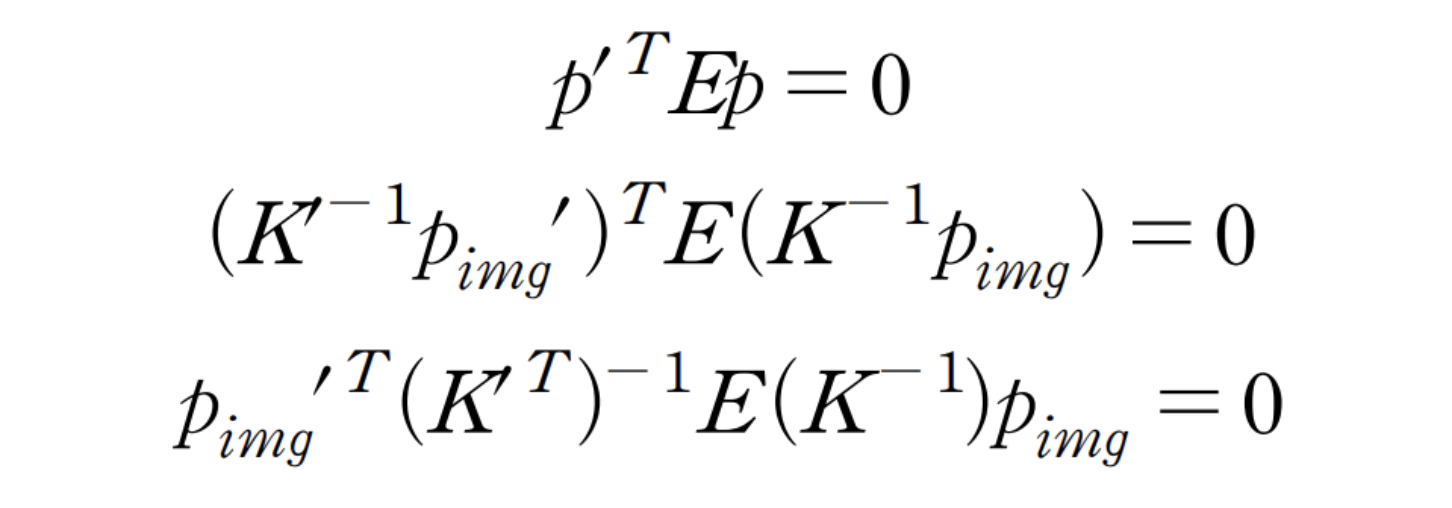
# x'T @ K^-1 T @ E @ K^-1 @ x = 0
ep_cons = (b @ K_inv @ E @ K_inv.T @ a.T)위의 epipolar constraint가 가장 작은 값을 가지는, 0에 가장 가까운 E를 골라주면 됩니다.
두 카메라 좌표축 사이의 3x3 회전행렬을 R, 3x1 평행이동 벡터를 t라 했을 때, 외부 공간상의 한 점을 두 카메라 좌표계에서 봤을 때의 관계를 P' = RP + t 으로 표현할 수 있습니다. 여기서 P는 왼쪽 카메라 좌표계의 3D 좌표, P'은 오른쪽 카메라 좌표계의 3D 좌표입니다.
Essential Matrix를 아래와 같이 표현할 수 있는데,
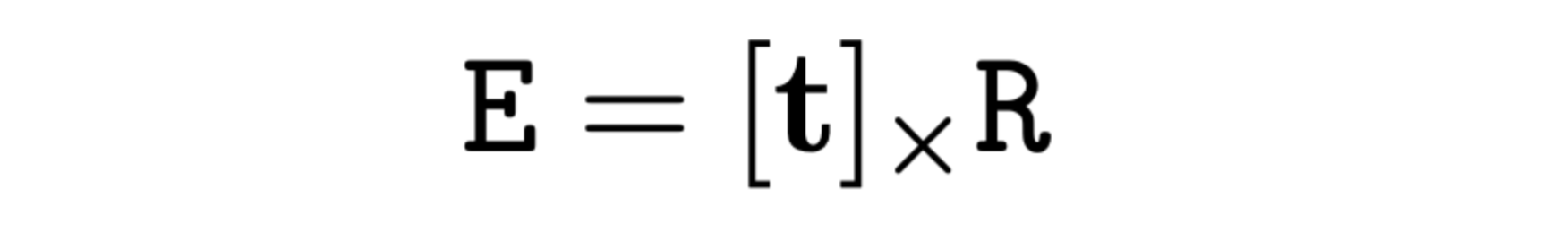
여기서 R은 Rotation Matrix 이며, [t]xR은 R과의 외적을 의미하는게 아니라, 먼저 R로 회전을 시킨 후 다음에 t와 외적을 시키는 일련의 변환을 의미합니다. 즉, P' = EP = [t]xRP = t x (RP) 입니다.
아래의 epipolar constraint(P' x E x P = 0)에 위의 식을 대입해봅시다.
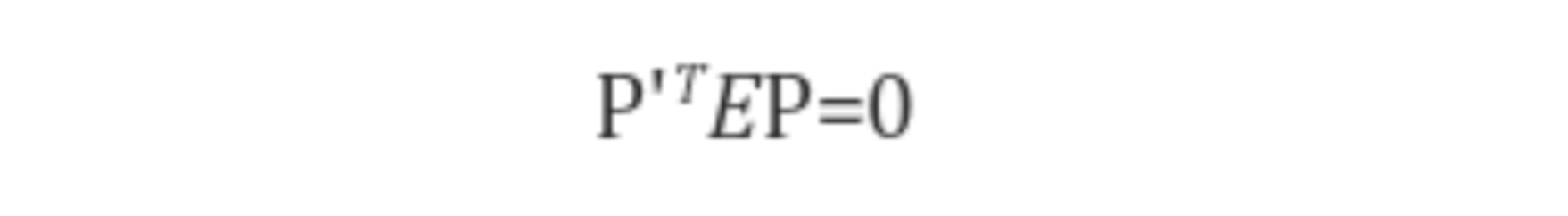
좌변에 E = [t]xR을 대입해 보면 다음과 같이 항상 0이 나옴을 알 수 있습니다.
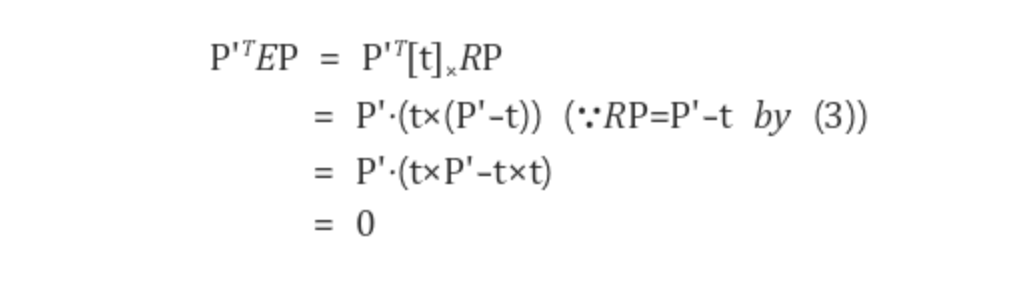
위 식을 카메라 좌표계에서 정규 좌표계로 바꾸면 (p' x E x p = 0)이 성립함을 알 수 있습니다
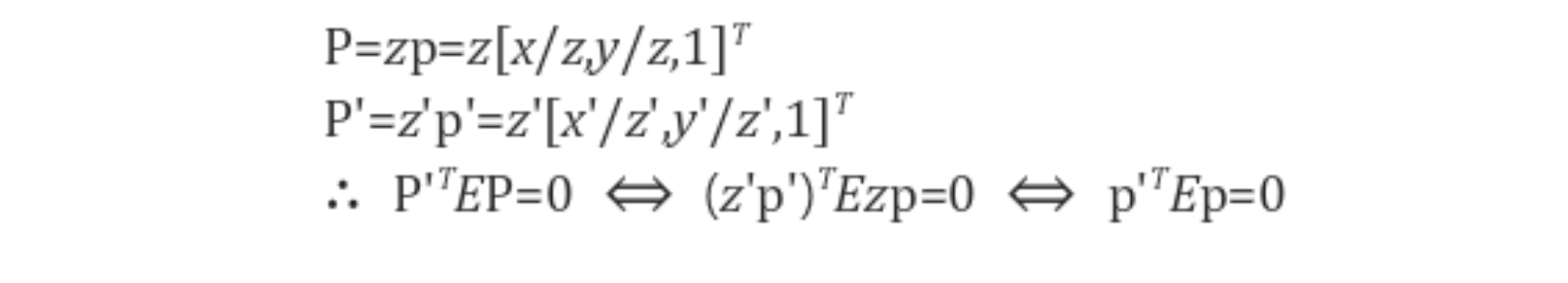
위에서 언급했듯이 애초에 cv2.findEssentialMat()이 디폴트로 5-point algorithm, method, intrinsic parameter, threshold를 파라미터 값으로 받아서 Essential Matrix를 만들기 때문에 결국 위에서 짠 Code2와 Code3는 의미가 없어졌습니다...
그래도 코드를 짜보면서 5 point algorithm, RANSAC을 이용하여 최적의 Essential Matrix을 구하는 과정(inlier가 가장 많은 E를 최종 선택), Essential Matrix를 구할 때 필요한 부분인 intrinsic parameter, epipolar constraint이 어떤 역할을 하는지 알 수 있었습니다.
Decompose essential matrix E to camera extrinsic[R|T]
이제 위에서 구한 Essential Matrix를 두 이미지에서의 매칭쌍으로부터 두 이미지의 상대적인 [R|t]를 구하기 위해 Essential Matrix를 Rotation Matrix와 Translation matrix로 분해해야 합니다. 이를 위해 특이값 분해(SVD)를 이용합니다. SVD는 고유값 분해(eigen decomposition)처럼 행렬을 대각화하는 방법입니다.
E = [t]xR 에는 자유도가 존재하는데 기본적으로 Rotation의 자유도가 3(x, y, z 축), Translation의 자유도가 2인 총 5의 자유도를 갖습니다. 5개의 자유도를 가진 E를 SVD를 통해 (3x3)행렬인 R과 t로 분해하면, 총 6개의 자유도를 갖는 것처럼 보이는데, SVD를 해보면 2개의 Singular Value가 동일하기 때문에 SVD는 고유하지 않습니다.
Essential Matrix에 SVD를 적용하면 아래와 같이 분해할 수 있습니다.
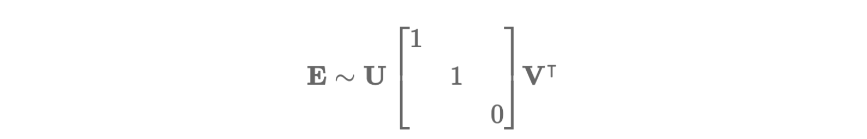
그리고 여기서 E는 아래와 같이 분해할 수 있습니다.
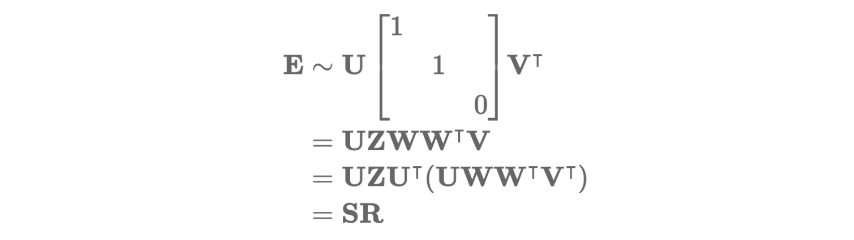
여기서 Orthogonal matrix인 W와 skew-symmetric matrix Z는 아래와 같습니다.
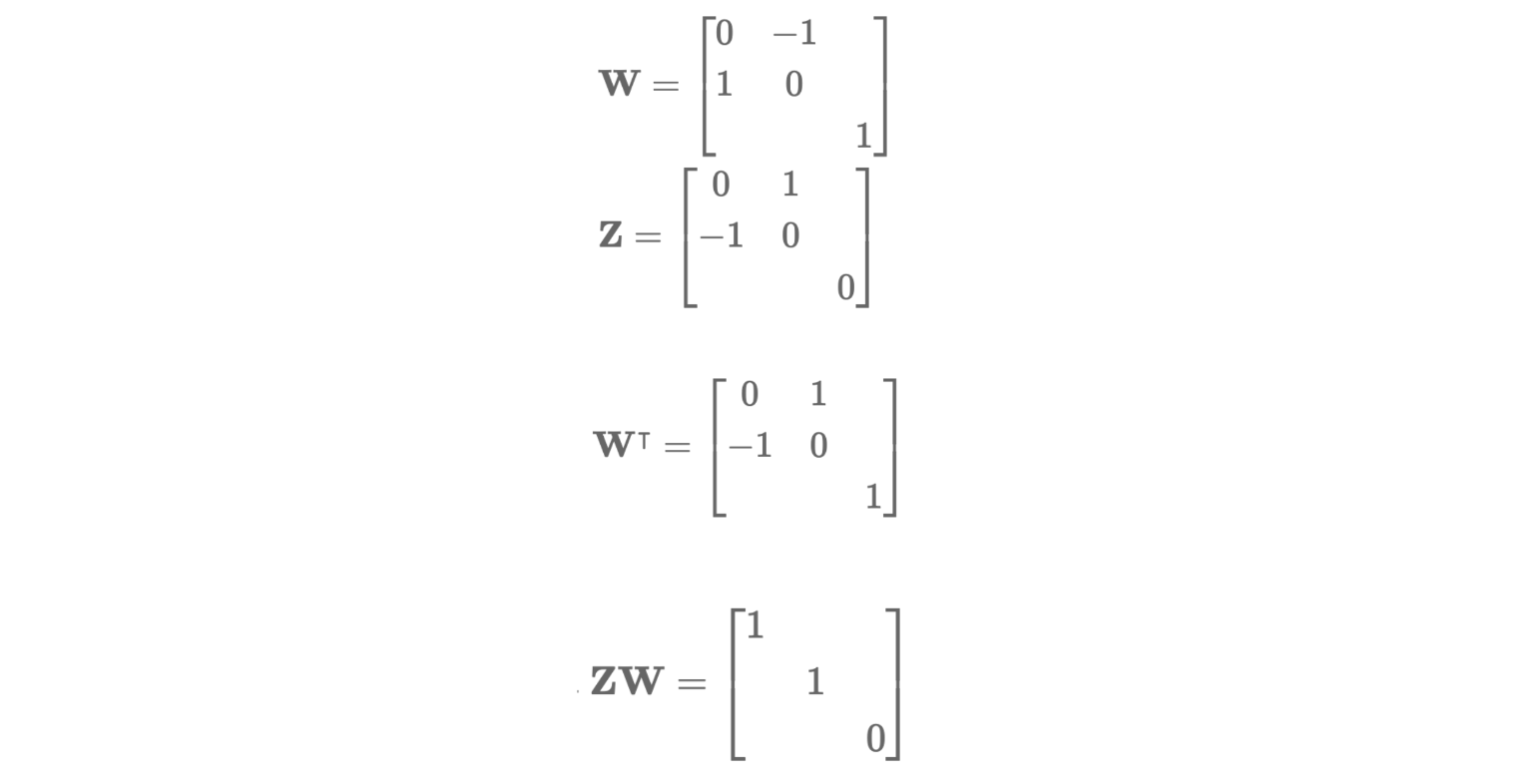
그리고 ZW는 아래와 같이 부호가 다른 2개의 행렬로 분해가 가능합니다.

따라서 Essential Matrix E는 아래와 같이 2개의 행렬로 분해가 가능합니다.

그리고 E = SR 이고
SR = S0 x R0 = S0 x R0' 이며,
S = +S0, -S0, R = R0, R0' 입니다.
따라서 Essential Matrix는 아래와 같이 나타낼 수 있습니다.

어느 카메라를 원점으로 잡는가에 따라 두 가지 해가 존재함을 의미합니다.
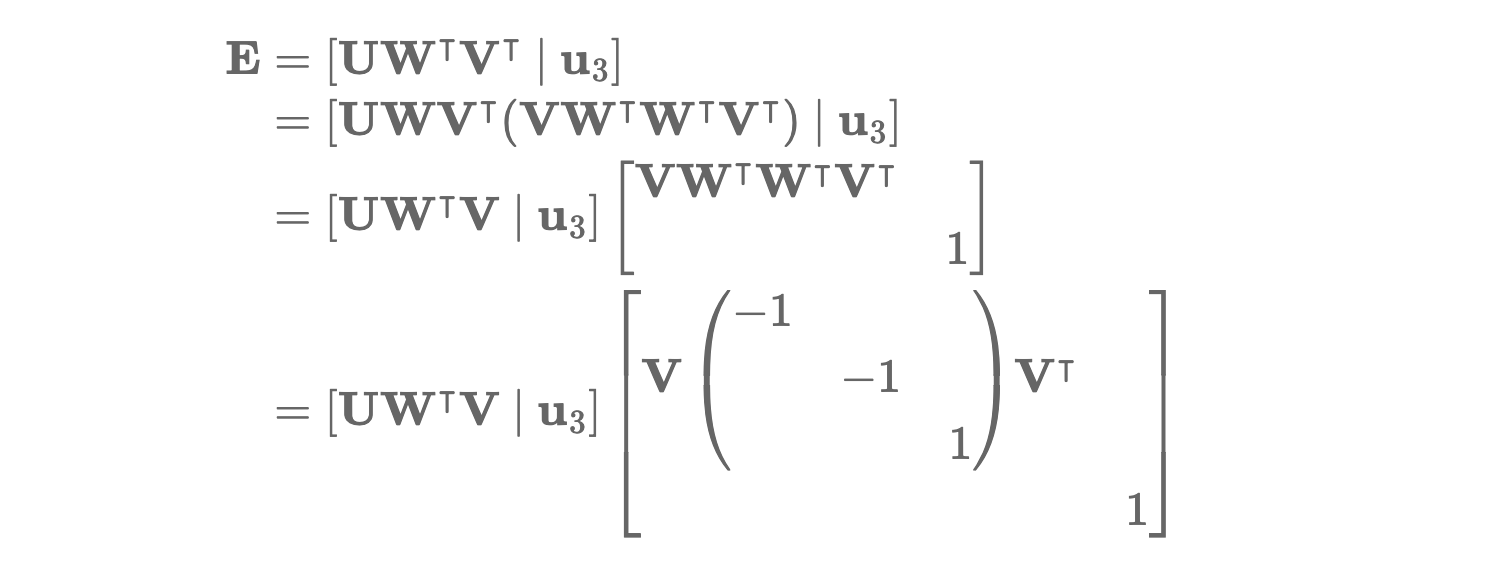
여기서 VWTWTVT 는 Baseline의 수직한 방향 2개를 상하대칭하는 행렬이 됩니다.
즉, Essential Matrix를 분해하면 Baseline을 축으로 180도 회전하는 형태로 4가지 변환 후보가 나오게 됩니다.
그리고 SVD에서 얻어진 Orthogonal Matrix인 W를 이용하면, 4개의 변환 후보를 얻을 수 있습니다.
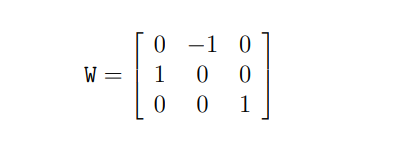
E를 SVD 하고, Orthogonal Matrix W 를 이용하여 4개의 변환 행렬 후보를 짜면 아래와 같은 결과를 얻을 수 있습니다.
# The four possible solutions for calibrated reconstruction from E
# Essential matrix to camera matrix
U, S, VT = np.linalg.svd(E, full_matrices=True)
W = np.array([
[0, -1, 0],
[1, 0, 0],
[0, 0, 1]
])
# camera matrix = P'= [UWVT | +u3] or [UWVT | −u3] or [UWTVT | +u3] or [UWTVT | −u3].
camera_matrix = np.array([
np.column_stack((U @ W @ VT, U[:,2])),
np.column_stack((U @ W @ VT, -U[:,2])),
np.column_stack((U @ W.T @ VT, U[:,2])),
np.column_stack((U @ W.T @ VT, -U[:,2]))])
print("The four possible solutions for calibrated reconstruction from E \n\n",camera_matrix)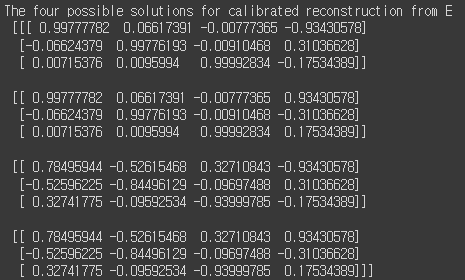
이 4개의 변환 중에서 무엇이 정확한 변환인지 확인하는 방법은, 이미지의 keypoint를 넣었을 때 모두 positive value가 나오는지 확인하면 됩니다. 왜냐면 정규화된 이미지 좌표를 넣어서 변환을 했을 때, base line보다 뒤에 있으면 negative value로 나오기 때문입니다. 즉, negative value가 나오면 카메라 뒤에 있게 되는 것입니다. 아래 그림에서 첫번째 변환이 정확한 변환을 나타냅니다.
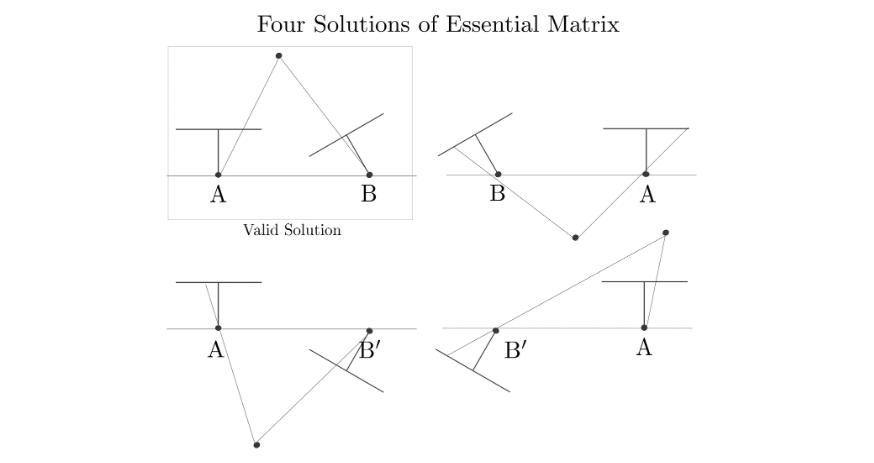
변환했을 때 negative value가 나오는 변환을 제외하면, 아래와 같은 결과를 얻을 수 있고, 두번째 변환이 정확한 변환인 것을 확인할 수 있습니다.
for i in range(4): # camera pose matrix , Rt x , 3d point HOMOGENIEUOUS
tmp = camera_matrix[i]
for j in range(len(p1)):
a = p1[j].flatten()
b = p2[j].flatten()
c = np.concatenate((a, b))
d = tmp@c.T # 3x4@4x4
if np.any(d<0):
print("made by camera matrix", i, "is not reconstructed point in front of both cameras")
break
하나의 코드로 작성하면 아래와 같습니다.
# The four possible solutions for calibrated reconstruction from E
def EM_Decomposition(E):
CM = np.array([[]])
# Essential matrix to camera matrix
U, S, VT = np.linalg.svd(E, full_matrices=True)
W = np.array([
[0, -1, 0],
[1, 0, 0],
[0, 0, 1]
])
# camera matrix = P'= [UWVT | +u3] or [UWVT | −u3] or [UWTVT | +u3] or [UWTVT | −u3].
camera_matrix = np.array([
np.column_stack((U @ W @ VT, U[:,2])),
np.column_stack((U @ W @ VT, -U[:,2])),
np.column_stack((U @ W.T @ VT, U[:,2])),
np.column_stack((U @ W.T @ VT, -U[:,2]))])
# camera pose matrix , Rt x , 3d point HOMOGENIEUOUS
for i in range(4):
tmp = camera_matrix[i]
for j in range(len(p1)):
a = p1[j].flatten()
b = p2[j].flatten()
c = np.concatenate((a, b))
d = tmp@c.T # 3x4@4x4
if np.any(d<0):
break
else:
CM = camera_matrix[i]
return CM
이렇게 구한 [R|t]도 cv2.recoverPose()를 이용하면 한번에 구할 수 있습니다.
cv2.recoverPose(): 입력된 essential matrix와 두 이미지에서의 매칭쌍으로부터 두 이미지의 상대적인 [R|t] 관계를 추출해 줍니다. cv2.decomposeEssentialMat()이 [R|t]를 유일하게 결정하지 못하고 해를 여러개 반환하는 반면, cv2.recoverPose()는 부가적인 기하학적 조건 검사를 통해 [R|t]를 유일하게 결정하여 반환해 줍니다.
Generate 3D point by Linear triangulation methods
지금까지 두 이미지 feature의 correspondence를 추정해주었고, 아직 3D 좌표는 알지 못합니다. 3D 좌표를 알기 위해선 Triangulation을 사용해야 합니다. 위에서 구한 [R|t]를 바탕으로 Triangulation 알고리즘을 사용하여 매칭점 쌍들에 대한 3차원 점을 계산할 수 있습니다.
아래의 그림에서 3D 좌표인 x1과 x2는 두 2D 이미지 상에서 관찰하는 위치가 됩니다. 그리고 x1와 x2를 연결하여 중점인 x를 구하게 됩니다. 만약 전혀 오차가 없는 상황이라면 x1과 x2는 일치 할 것입니다. 이러한 방식으로 3D 좌표를 구합니다.
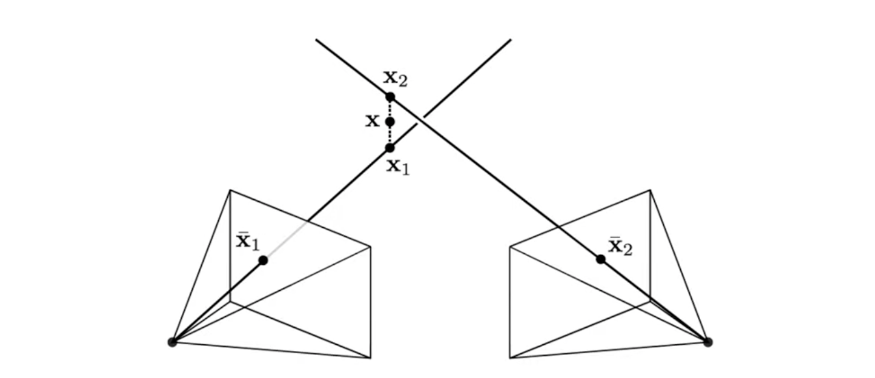
x와 x'이 image correspondence의 set일 때, 이론적으로는 x, x'를 Back-projection하여 얻은 두 직선의 교차점을 통해 X를 계산할 수 있으나 실제 데이터는 노이즈가 존재하기 때문에 두 Back-projection 직선이 교차하지 않습니다. 또한 노이즈로 인해 두 이미지 평면 상에서 Epipolar Line l, l' 또한 x, x'와 만나지 않습니다. 이를 해결하기 위해서 두 Back-projection 직선들에 동시에 수직인 최단거리 직선을 구한 다음 최단거리 직선의 중점(mid-point)를 계산하여 X를 계산하는 방법이 존재합니다.
x, P, X 를 아래과 같이 정의하고,
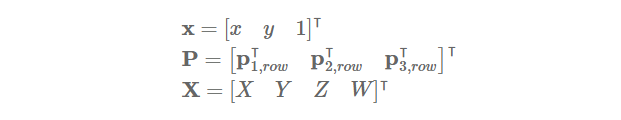
Camera Matrix P에 대하여, 3D 좌표인 X는 x = PX, x'=PX 로 부터 아래와 같은 식을 만족합니다..
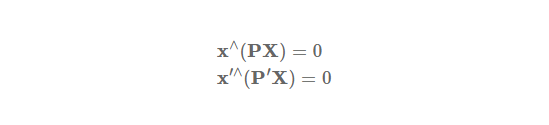
p(i,row)T 를 P의 i번째 행이라 했을 때, x^(PX)를 전개한 후 정리하면, 아래와 같습니다.
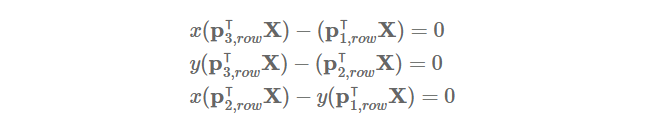
x'^(P'X)도 구하고 X에 대하여 linear system으로 다시 작성하면, 아래와 같이 AX=0 형태로 정리할 수 있습니다.
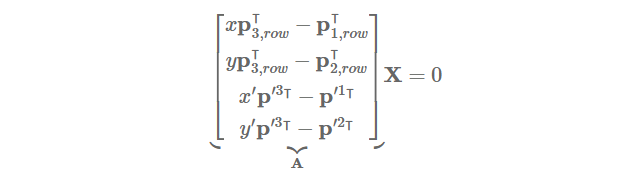
노이즈가 없는 경우에는 유일한 X를 계산할 수 있지만, 노이즈가 존재하는 경우에는 그렇지 못합니다.
따라서 A를 SVD하여 분해하고, U x S x VT 에서 VT의 각 열은 Ax = 0의 해를 갖습니다.
그리고 eigen value의 값이 최소가 되는 열을 선택하면 됩니다.
# intrinsic parameter
Rt0 = np.hstack((np.eye(3), np.zeros((3, 1))))
skew = 0.0215878
K = np.array([[3092.8, skew, 2016], [0, 3092.8, 1512], [0,0,1]])
Rt1 = K @ CameraMatrix
# Rescale to Homogeneous Coordinate
def rescale_point(pts1, pts2, length):
a = [[]]
b = [[]]
for i in range(length):
tmp1 = pts1[i].flatten()
tmp1 = np.append(tmp1, 1)
a = np.append(a, tmp1)
tmp2 = pts2[i].flatten()
tmp2 = np.append(tmp2, 1)
b = np.append(b, tmp2)
a = a.reshape((length),3)
b = b.reshape((length),3)
return a, b
p1, p2 = rescale_point(p1, p2, len(p1))
# Triangulation
def LinearTriangulation(Rt0, Rt1, p1, p2):
A = [p1[1]*Rt0[2,:] - Rt0[1,:], # x(p 3row) - (p 1row)
-(p1[0]*Rt0[2,:] - Rt0[0,:]), # y(p 3row) - (p 2row)
p2[1]*Rt1[2,:] - Rt1[1,:], # x'(p' 3row) - (p' 1row)
-(p2[0]*Rt1[2,:] - Rt1[0,:])] # y'(p' 3row) - (p' 2row)
A = np.array(A).reshape((4,4))
AA = A.T @ A
U, S, VT = np.linalg.svd(AA) # right singular vector
return VT[3,0:3]/VT[3,3]
p3ds = []
for pt1, pt2 in zip(p1, p2):
p3d = LinearTriangulation(Rt0, Rt1, pt1, pt2)
p3ds.append(p3d)
p3ds = np.array(p3ds).T위 코드는 Direct Linear Transform을 사용하였습니다.
cv2.triagulatePoints() 로도 한번에 구할 수 있습니다.
# Generate 3D point by implementing Triangulation
Rt0 = np.hstack((np.eye(3), np.zeros((3, 1))))
Rt1 = np.hstack((R, t))
Rt1 = np.matmul(K, Rt1)
pt1 = np.transpose(p1)
pt2 = np.transpose(p2)
p3d = cv2.triangulatePoints(Rt0, Rt1, pt1, pt2)
p3d /= p3d[3] # Homogeneous CoordinateTwo view visualization
여기까지 구한 3D 좌표를 시각화하면 아래와 같습니다.
X = np.array([])
Y = np.array([])
Z = np.array([]) #120
X = np.concatenate((X, p3ds[0]))
Y = np.concatenate((Y, p3ds[1]))
Z = np.concatenate((Z, p3ds[2]))
fig = plt.figure(figsize=(15,15))
ax = plt.axes(projection='3d')
ax.scatter3D(X, Y, Z, c='b', marker='o')
plt.show()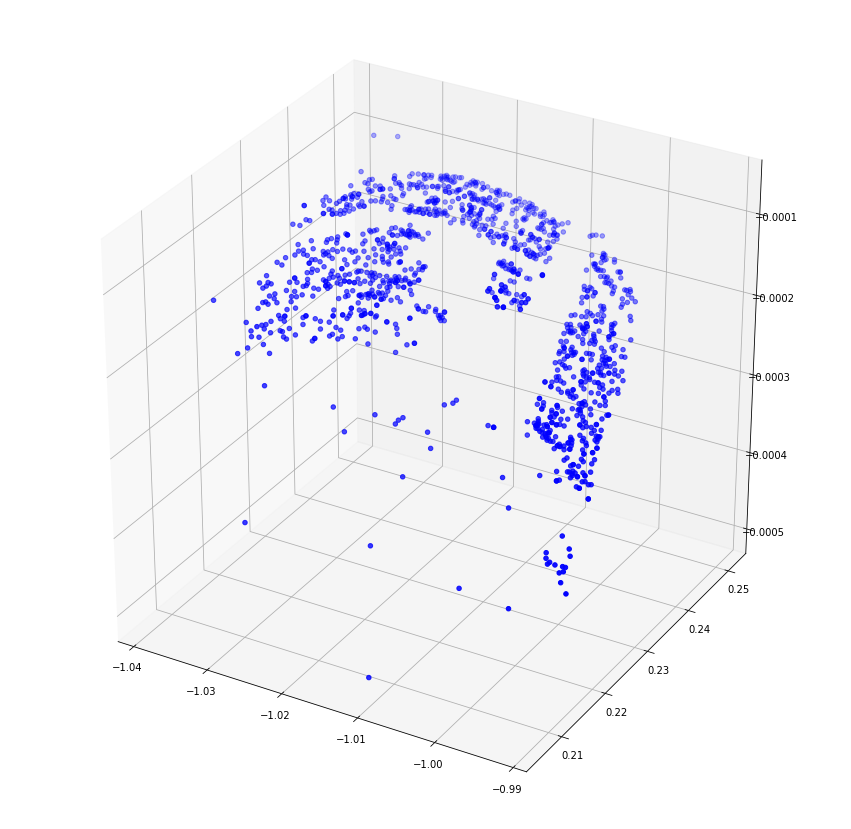
지금까지의 코드를 정리하면 아래와 같습니다.
import cv2
import sys
import numpy as np
from matplotlib import pyplot as plt
img_path = '/content/drive/MyDrive/Colab_Notebooks/GIST/nutellar2/'
img1_name = 'nutella13.jpg'
img2_name = 'nutella14.jpg'
#############################################################
#################### Feature Extraction #####################
#############################################################
# Load image
def load_image(img_path, img1_name, img2_name):
img1 = cv2.imread(img_path + img1_name)
img2 = cv2.imread(img_path + img2_name)
img1 = cv2.cvtColor(img1,cv2.COLOR_BGR2RGB)
img2 = cv2.cvtColor(img2,cv2.COLOR_BGR2RGB)
return img1, img2
# Find feature correspondence with SIFT
def SIFT(img1, img2):
sift = cv2.xfeatures2d.SIFT_create()
img1_kp, img1_des = sift.detectAndCompute(img1, None)
img2_kp, img2_des = sift.detectAndCompute(img2, None)
bf = cv2.BFMatcher()
matches = bf.knnMatch(img1_des, img2_des, k=2)
matches_good = [m1 for m1, m2 in matches if m1.distance < 0.95*m2.distance]
sorted_matches = sorted(matches_good, key=lambda x: x.distance)
res = cv2.drawMatches(img1, img1_kp, img2, img2_kp, sorted_matches, img2, flags=2)
# drwa matches
plt.figure(figsize=(15, 15))
plt.imshow(res)
plt.show()
return matches_good, img1_kp, img2_kp
#############################################################
################ Essential Matrix Estimation ################
#############################################################
# Preprocessing
def Estimation_E(matches_good, img1_kp, img2_kp):
query_idx = [match.queryIdx for match in matches_good]
train_idx = [match.trainIdx for match in matches_good]
p1 = np.float32([img1_kp[ind].pt for ind in query_idx]) # 픽셀 좌표
p2 = np.float32([img2_kp[ind].pt for ind in train_idx])
# Find Essential Matrix and Inliers with RANSAC, Intrinsic parameter
E, mask = cv2.findEssentialMat(p1, p2, method=cv2.RANSAC, focal=3092.8, pp=(2016, 1512), maxIters = 500, threshold=1)
p1 = p1[mask.ravel()==1] # left image inlier
p2 = p2[mask.ravel()==1] # right image inlier
return E, p1, p2
#############################################################
############### Essential Matrix Decomposition ##############
############# The four possible solutions from E ############
#############################################################
def EM_Decomposition(E, p1,p2):
CM = np.array([[]])
# Essential matrix to camera matrix
U, S, VT = np.linalg.svd(E, full_matrices=True)
W = np.array([
[0, -1, 0],
[1, 0, 0],
[0, 0, 1]
])
# camera matrix = P'= [UWVT | +u3] or [UWVT | −u3] or [UWTVT | +u3] or [UWTVT | −u3].
camera_matrix = np.array([
np.column_stack((U @ W @ VT, U[:,2])),
np.column_stack((U @ W @ VT, -U[:,2])),
np.column_stack((U @ W.T @ VT, U[:,2])),
np.column_stack((U @ W.T @ VT, -U[:,2]))])
# camera pose matrix , Rt x , 3d point HOMOGENIEUOUS
for i in range(4):
tmp = camera_matrix[i]
for j in range(len(p1)):
a = p1[j].flatten()
b = p2[j].flatten()
c = np.concatenate((a, b))
d = tmp@c.T # 3x4@4x4
if np.any(d<0):
break
else:
CM = camera_matrix[i]
return CM
#############################################################
###### Generate 3D point by implementing Triangulation ######
#############################################################
# Rescale to Homogeneous Coordinate
def rescale_point(pts1, pts2, length):
a = [[]]
b = [[]]
for i in range(length):
tmp1 = pts1[i].flatten()
tmp1 = np.append(tmp1, 1)
a = np.append(a, tmp1)
tmp2 = pts2[i].flatten()
tmp2 = np.append(tmp2, 1)
b = np.append(b, tmp2)
a = a.reshape((length),3)
b = b.reshape((length),3)
return a, b
# intrinsic parameter K
def initialize_CM(CM):
Rt0 = np.hstack((np.eye(3), np.zeros((3, 1))))
skew = 0.0215878
K = np.array([[3092.8, skew, 2016], [0, 3092.8, 1512], [0,0,1]])
Rt1 = K @ CameraMatrix
return Rt0, Rt1
# Triangulation
def LinearTriangulation(Rt0, Rt1, p1, p2):
A = [p1[1]*Rt0[2,:] - Rt0[1,:], # x(p 3row) - (p 1row)
-(p1[0]*Rt0[2,:] - Rt0[0,:]), # y(p 3row) - (p 2row)
p2[1]*Rt1[2,:] - Rt1[1,:], # x'(p' 3row) - (p' 1row)
-(p2[0]*Rt1[2,:] - Rt1[0,:])] # y'(p' 3row) - (p' 2row)
A = np.array(A).reshape((4,4))
AA = A.T @ A
U, S, VT = np.linalg.svd(AA) # eigen vector
return VT[3,0:3]/VT[3,3]
def make_3dpoint(p1, p2):
p3ds = []
for pt1, pt2 in zip(p1, p2):
p3d = LinearTriangulation(Rt0, Rt1, pt1, pt2)
p3ds.append(p3d)
p3ds = np.array(p3ds).T
return p3ds
#############################################################
######################### visualize #########################
#############################################################
def visualize_3d(p3ds):
X = np.array([])
Y = np.array([])
Z = np.array([]) #120
X = np.concatenate((X, p3ds[0]))
Y = np.concatenate((Y, p3ds[1]))
Z = np.concatenate((Z, p3ds[2]))
fig = plt.figure(figsize=(15,15))
ax = plt.axes(projection='3d')
ax.scatter3D(X, Y, Z, c='b', marker='o')
plt.show()
# run
img1, img2 = load_image(img_path, img1_name, img2_name)
matches_good, img1_kp, im2_kp = SIFT(img1, img2)
E, p1_inlier, p2_inlier = Estimation_E(matches_good, img1_kp, img2_kp)
CameraMatrix = EM_Decomposition(E, p1_inlier, p2_inlier)
Rt0, Rt1 = initialize_CM(CameraMatrix)
p1, p2 = rescale_point(p1_inlier, p2_inlier, len(p1_inlier))
point3d = make_3dpoint(p1, p2)
visualize_3d(point3d)Perspective 3 Point Algorithm
Perspective 3 Point Algorithm은 Intrinsic Parameter를 알고, 이미지 feature point(2D point)와 해당되는 3D point을 가지고 있을 때, 카메라의 위치 및 촬영 각도를 파악하는 방법입니다.
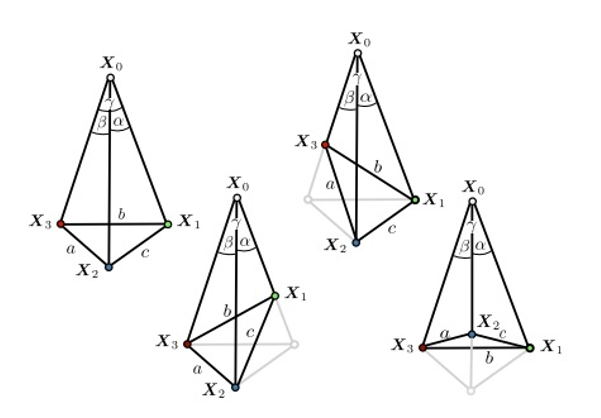
이 3차원 모델 상의 두 점인 p0와 p1이 카메라 센터에서 바라볼 때 나오는 사이각은 2차원 이미지 상의 같은 두 점인 x0와 x1에서 나오는 각도가 같다는 점을 이용하여 반복적으로 같은 각도가 같은 부분을 찾아 Camera pose(c)를 구할 수 있습니다. 하지만 실제 데이터는 일부 오류가 있기 때문에 RANSAC을 이용하여 오류 부분을 제거하고, 최적의 위치를 찾아내야 합니다.
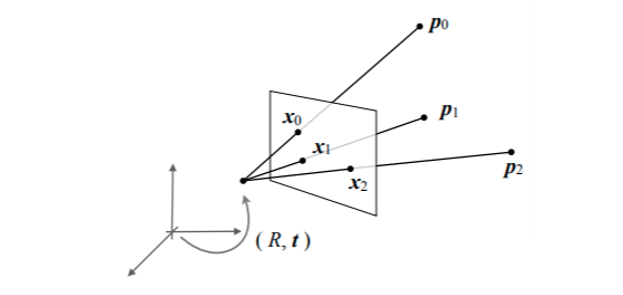
위의 그림처럼 3D point와 2D point가 주어졌을 때 카메라 R,t를 찾는 과정이고, 한개의 카메라에 대해서 3개의 좌표와 3개의 포인트가 주어졌을 때, 카메라의 pose를 구합니다. (R,t)
x0과 x1의 좌표로 arccos(x0 . x1)을 통해 사이각를 구할 수 있고, p0와 p1의 좌표를 통해서 p0p1의 길이를 구할 수 있습니다.
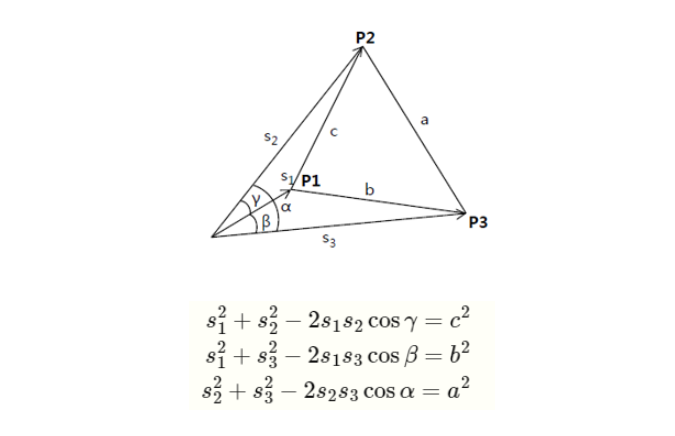
a, b, c에 대해 cosine 제 2법칙으로 위와 같은 식을 만들 수 있고,
s2 = u x s1, s3 = v x s2 로 치환하고, s1에 대한 식으로 정리하면 아래와 같이 나타낼 수 있습니다.
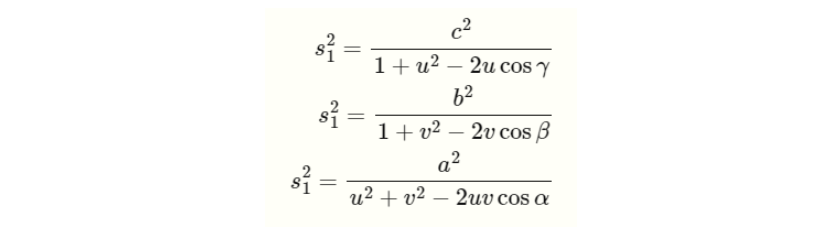
위 식은 아래와 같이 정리할 수 있고
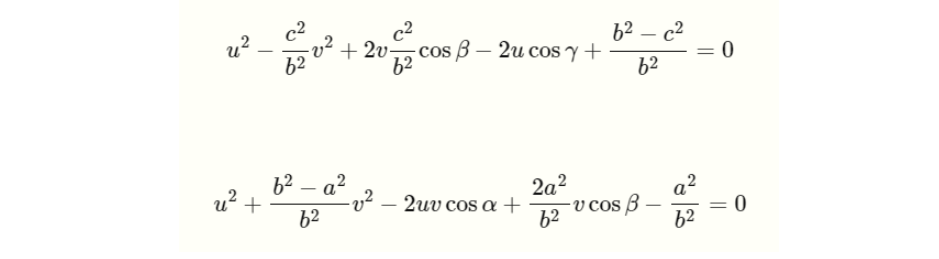
위의 두번째 식에서, u에 대한 해를 구하면 아래와 같이 u를 표현할 수 있습니다.
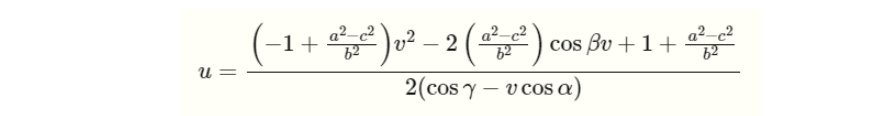
그리고 u를 첫번째 식에 대입하면 아래와 같은 식으로 표현할 수 있습니다.
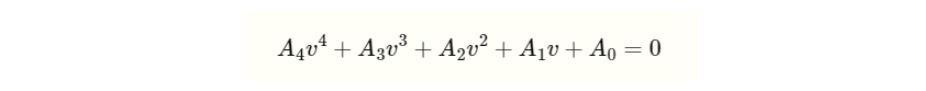
여기서 각 차수에 대한 상수항은 아래와 같습니다.
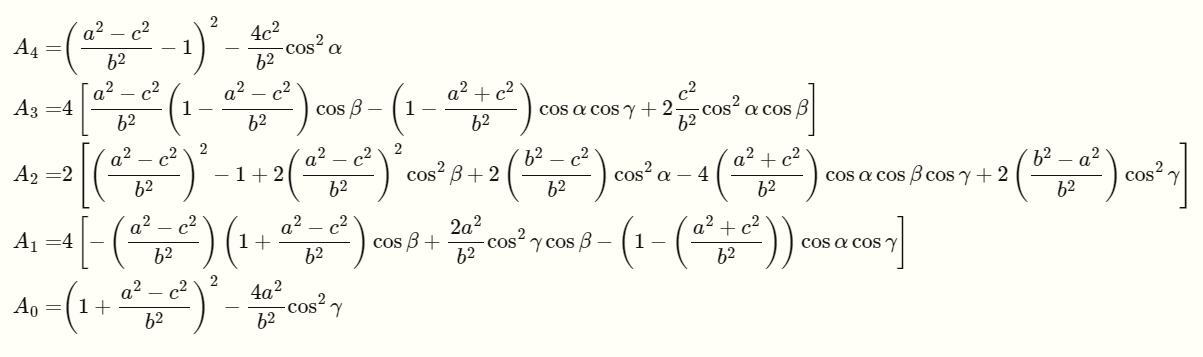
위의 식으로부터 나온 4개의 해 중에서, 하나의 해만 만족하기 때문에 여기서 RANSAC을 이용하여 최적의 모델을 구한다.
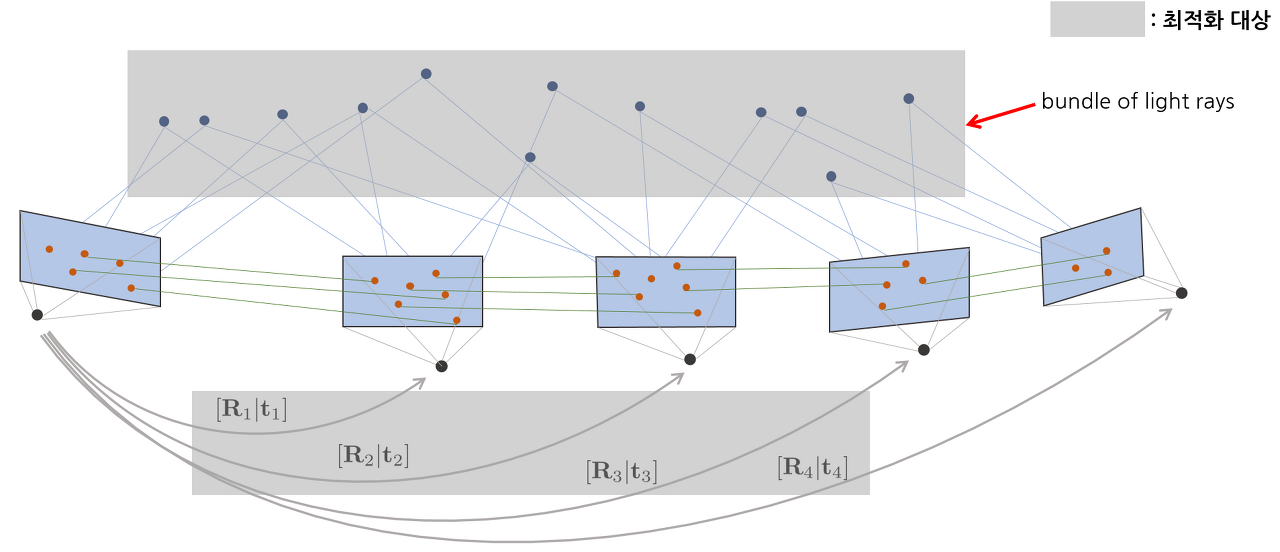
Bundle Adjustment
Bundle Adjustment는 위에서 구한 3D point들을 키프레임 이미지 들에 투영시킨 위치와 영상 프레임에서 실제 관측된 위치의 차이(Reprojection error)를 최소화 시키도록 3D point의 위치와 카메라 위치를 최적화 하는 과정입니다. 여기서 Bundle은 하나의 point가 아닌 여러개의 point들(여러 카메라 시점에 대한)의 Reprojection error를 말합니다.
Bundle Adjustment를 하는 이유는 3D 지형과 Camera pose의 위치 추정 개선을 위함입니다.
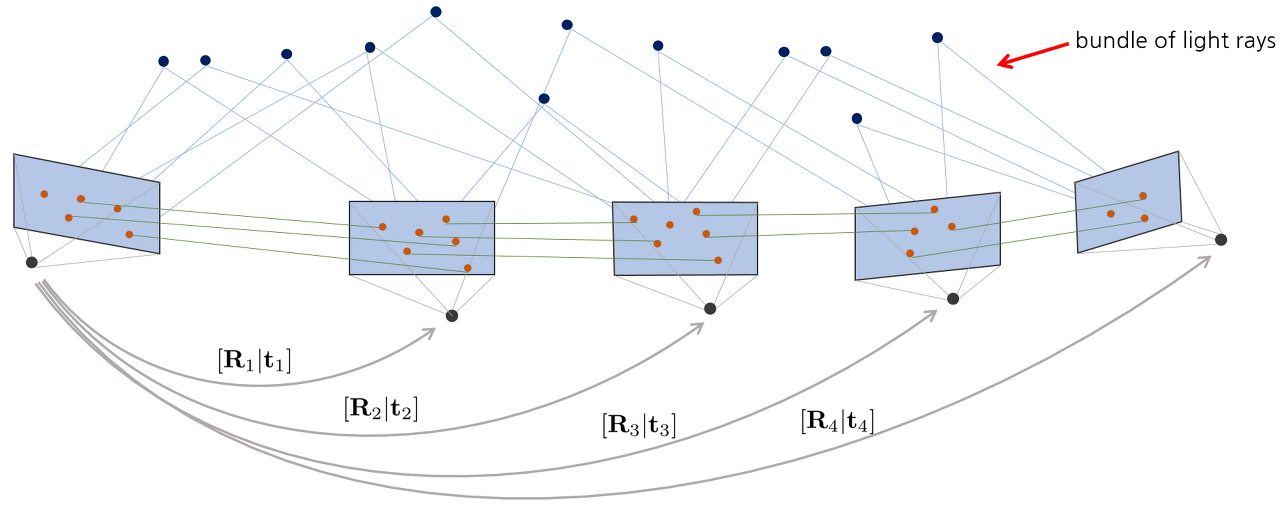
즉, 위 그림과 같이 연속적인 카메라 영상 + 매칭 쌍이 주어졌을 때 Camera pose 전체와 월드 좌표계의 점들 전체에 대한 최적의 위치를 찾는 방법입니다.
Ref.
Multiple View Geometry in Computer Vision Second Edition, Richard Hartley Australian National University, Cambridge University Press 2000, 2003, p257 ~ p270
SfM : https://darkpgmr.tistory.com/
perspective 3 point algorithm : https://jingnanshi.com/blog/pnp_minimal.html
.