SIFT (Scale Invariant Feature Transform)
SIFT란? (Scale Invariant Feature Transform)
크기, 회전, 조도, affine의 변화 및 noise에 불변하는 특징을 추출하는 알고리즘이다. 이는 다음과 같은 절차로 이루어 진다.

Find Scale-Space Extrema
우선 크기에 불변하는 특징을 추출하기 위해서, 각 원본 이미지를 1/2 배씩 다운 샘플링 하면서 이미지를 나열한다. 이처럼 같은 이미지에 대해 scale space를 다양하게 하는 이유는 스케일에 따라 세부적인 내용에 집중할수도, 전체적인 구조에 집중할 수도 있기 때문이다. 그렇기 때문에 크기에 불변하는 특징을 모두 추출하기 위해서는 다양한 scale space로 부터 feature를 추출해야 한다.
또한 사진이 멀리서 찍혔다거나, 포커스가 맞지 않거나 다양한 이유로 생기는 noise를 표현하기 위해서 점진적으로 blur시킨다. 이러한 이유 뿐만 아니라 blur는 scale space에도 영향을 미치는데, 이미지를 블러링 함으로써 디테일은 줄고, 모호해지므로 이미지의 사이즈를 유지시키면서 scale을 크게 할 수 있다.
그렇다면 어떻게 이미지에 blur를 적용시킬까? 가우시안 필터를 이용해서 가능하다. 잠시 가우시안의 분포도를 확인해보자.
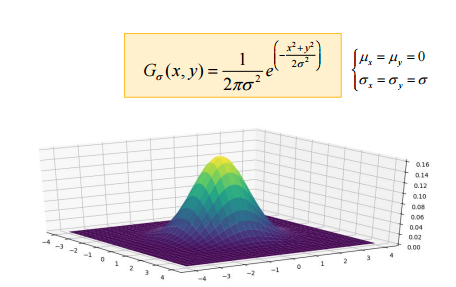
가우시안을 이용한 필터가 LPF(Low-pass filter)임을 알 수 있다. 기존 이미지와 이 가우시안 필터를 convolution연산을 하면 고주파 영역을 제거함으로써 노이즈가 제거되고(노이즈를 엣지로 착각하는것을 방지), 경계선이 흐려진다. 그렇기 때문에 가우시안 필터를 이용함으로써 블러효과를 얻을 수 있다. 이 효과는 표준편차가 더 커질수록 필터링 되는 비중이 커지는데, 표준편차의 값을 조정하며 블러의 정도를 조정할 수 있다.
위에 서술한 scale space의 특성을 이용하여 다음과 같이 scale space를 만든다.
upsampling -> ( (점진적 blur x k회) -> down sampling ) x n회
아래는 그에 대한 결과이다.

이와 같은 과정을 거침으로써 이미지의 크기에 불변하는 특성을 갖게 된다.
DoG연산
중요한 feature(key point)가 어디에 존재할까? 엣지와 코너 즉, 변화량이 매우 큰 곳에서 그러한 특징이 존재할 가능성이 높을것이다. 변화량을 알기 위해서 2차 미분을 진행하여 엣지를 얻는 LoG방식이 존재한다. 하지만 미분이 너무나도 연산이 비싸기 때문에 이에 근사하는 DoG를 사용한다. 이는 열 확산 방정식에 의해 증명이 가능한데 이 과정에서 DoG(Difference of gaussain)가 scale 불변성을 보장하는 scale 정규화 과정을 자연스럽게 포함하는 것을 알 수 있다.
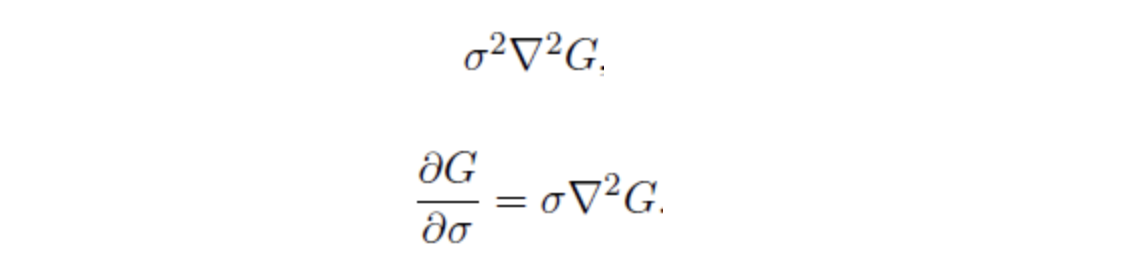
여기서 열 확산 방정식을 응용하면, 아래와 같다.
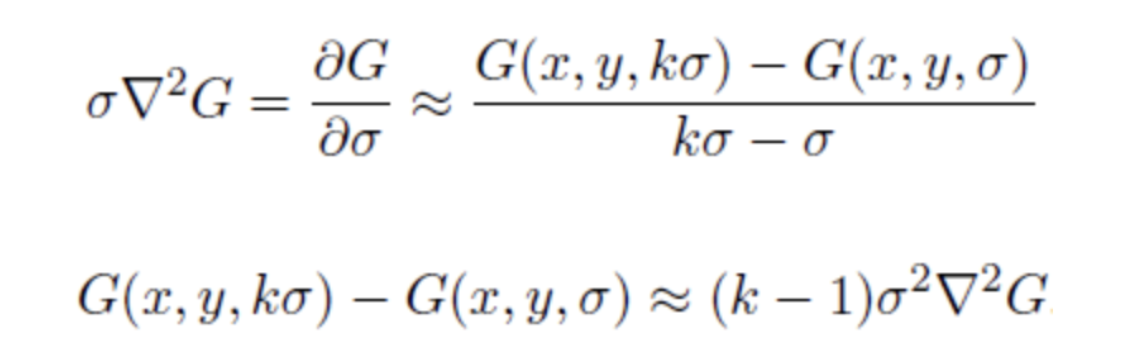
따라서 DoG를 통해 손쉽게 엣지와 코너가 강조된 데이터를 얻을 수 있다. 이 과정에서 DOG의 특성에 의해 2개의 이미지가 연산되어 하나의 DOG가 도출됨에 유의해야한다. 같은 scale의 다른 blur정도(gaussian의 표준편차의 값에 차이)를 갖는 이미지셋인 octave내에서 이 과정이 진행된다. 그 결과는 다음과 같다.
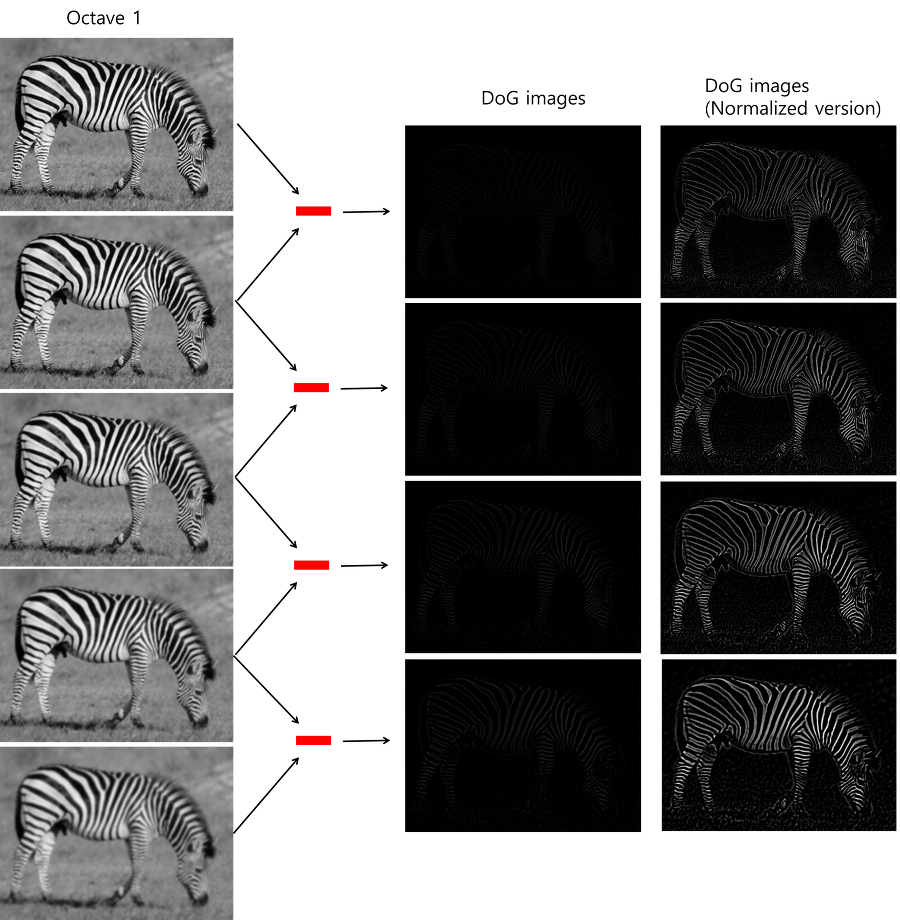
Keypoint 들 찾기
이제 엣지와 코너를 찾았다. 하지만 이 엣지와 코너가 모두 keypoint인것은 아니다. keypoint란 DoG의 결과 중에서도 극대, 극소값인 경우가 많다. 왜냐하면 이는 매우 안정적으로 이미지의 특징을 나타내기 때문이다. 그렇기 때문에 DoG의 결과 중에서도 극대, 극소를 갖는 포인트를 후보 keypoint라고 한다.
극대 극소를 어떻게 찾을까? 같은 octave내의 인접한 이미지 2장 및 후보 keypoint 이미지에 대해서 후보 keypoint의 좌표와 동일한 좌표를 중심으로 하는 3X3크기의 윈도우를 비교한다. 만약 3개의 3x3크기의 윈도우 내에서 그 keypoint값이 극대값 혹은 극소값이라면 keypoint일 가능성이 있는 점으로 분류한다. (총 3x3x3 - 1(비교 point) = 26개를 비교함)
지금까지 우리는 픽셀 단위로 계산하였다. 엣지 검출도, 후보 keypoint 필터링도 모두 픽셀단위였다. 하지만 실제 그소값, 극대값은 픽셀 사이 즉, subpixel에 존재할 수 있다. 이에 대한 정확한 위치를 알기 위해서 테일러 2차 전개를 통해 실제 극값을 찾아낸다.

이를 x로 미분하여 0이 되는 x의 값이 극값의 위치가 된다. 즉 극값의 위치는 다음과 같다.
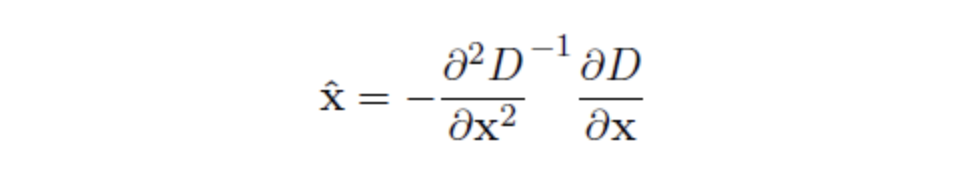
나쁜 keypoint 제거
이렇게 얻은 극값이 모두 keypoint인 것은 아니다. 그렇기 때문에 일부 의미없는 keypoint를 제거해주어야 한다. 그 기준은 다음과 같다.
낮은 contrast를 갖는 keypoint
더 정확한 extrema를 얻기 위해 테일러 전개를 통해 그 점의 contrast를 구해서 key를 걸러낸다.
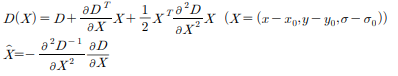
엣지 위에 존재하는 keypoint
Harris corner detection을 통해서 edge를 제거한다. DoG가 엣지를 찾아낼 때 매우 민감하게 찾아내므로 약간에 노이즈에 민감하게 반응할 수 있고, edge보다 corner가 더 이미지에 대한 특징을 잘 담아 내기 때문에 안정적인 corner만 남겨두는 것이다.
코너임을 판별하기 위해서는 수직과 수평에 대한 gradeint를 계산해야 한다. 이렇게 계산된 gradient가 두 방향에 대해서 모두 크다면 corner라고 판별할 수 있다. 이 과정에서 Harris Edge Detection과 eigenvalue가 사용된다. 하나의 윈도우를 가지고 움직이면서 그 안의 이미지의 값의 합이 어떻게 변화하는지에 따라 edge과 corner를 판별하게 된다. // 수학적인 부분은 스킵..ㅠㅠ

다음은 이를 적용한 결과이다.
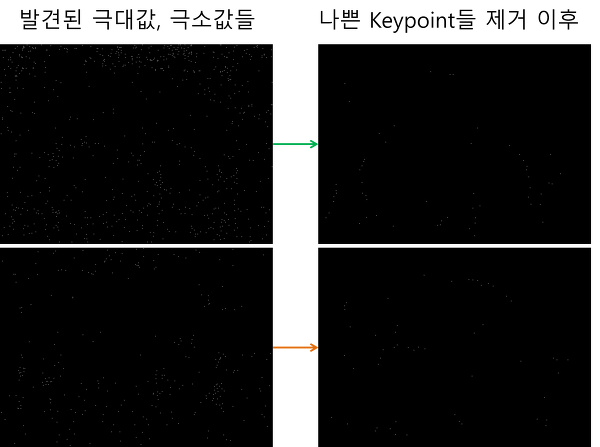

이 과정을 거침 으로서 상당히 많은 후보 keypoint들이 제거되고 유의미한 keypoint만 남았음을 확인할 수 있다.
이제 적당한 keypoint를 찾았으니 scale invariant한 keypoint에 rotation invariance를 적용시킬 차례이다. 이는 keypoint 주변의 그래디언트 방향 및 크기를 구하고, 가장 도드라지는 방향을 keypoint 방향으로 할당시켜줌으로써 진행된다.
keypoint 주변에 윈도우를 만들어 준 이후, 가우시안 블러링을 진행한다. 이후, 그 윈도우 안의 모든 픽셀에 대해 그래디언트 방향과 크기를 구한다.

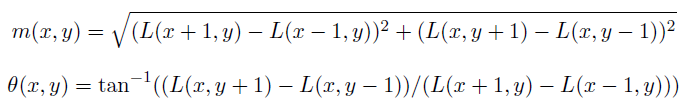
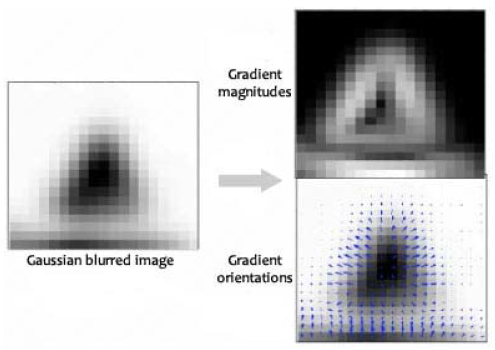
이후, keypoint와 픽셀간의 거리에 대한 가중치를 적용시킨다.

이렇게 나타난 최종 방향 및 크기에 대해서 10도씩 그룹핑을 한다. 그리고 가장 큰 값을 갖거나, 일정 threshold이상의 크기를 갖는 방향을 keypoint의 방향으로 설정한다.
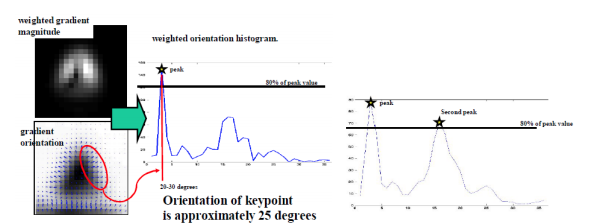
이렇게 함으로써 keypoint들이 rotation-invariant한 특성을 갖게 됨을 알 수 있다.
최종 SIFT 특징들 산출하기(key point, key point desciptor)
지금까지 스케일 불변성과 회전 불변성을 갖는 keypoint의 위치와 스케일의 방향을 구했다. 이제 두 사진을 비교하면서 공통된 특징을 갖는 부분(key point)를 매칭시킨다. 이 과정은 keypoint의 지문간의 비교로 이루어지는데, 이 지문을 key point descriptor라고 한다.
key point descriptor란, key point를 포함하는 16 x 16칸의 정보를 의미하는데, 실제 하나의 keypoint만으로는 매칭이 어렵기 때문이다. (확률적인 요소가 존재할 요소가 다분하다) 때문에 keypoint를 기준점으로 설정하고 16 x 16칸의 정보를 이용해서 매칭할 수 있도록 지문을 남겨두는 것이다.
16 x 16칸을 16개의 4x4크기의 window로 표현하고, 이전 keypoint에서 gradient의 방향과 크기를 도출하였던 것 처럼 4x4 윈도우 내에서의 gradient의 방향과 크기를 설정하고, (360 / 8 = 45)도씩 그룹핑 하여 4x4크기 window의 gradient 크기 및 방향을 구한다.
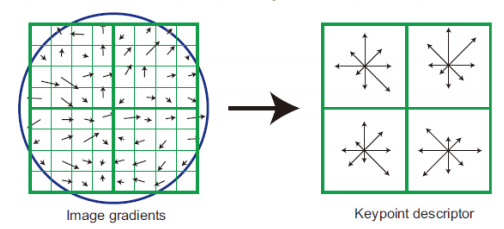
이렇게 생성된 keypoint descriptor를 비교하면서 차이가 작은 keypoint descriptor 쌍이 매칭되는 특징이 된다. 이때 유클리드 거리로 1차 매칭을 하고, 가까운 키의 비율을 통해 matching이 제대로 되었는지 확인한다. (0.8 이상이 되면 그 key는 버린다)
inlier와 outlier를 구별해서 inlier끼리 clustering을 통해 이를 검증하는 작업을 거친 이후에 비로소 SIFT가 끝나게 된다.
실제 구현
다음은 SIFT를 opencv를 이용하여 구현한 예시이다.
import cv2
import numpy as np
from matplotlib import pyplot as plt
img1 = cv2.imread('/content/drive/MyDrive/Colab_Notebooks/GIST/gerrard-hall/images/IMG_2331.JPG')
img2 = cv2.imread('/content/drive/MyDrive/Colab_Notebooks/GIST/gerrard-hall/images/IMG_2332.JPG')
img1 = cv2.cvtColor(img1,cv2.COLOR_BGR2GRAY)
img2 = cv2.cvtColor(img2,cv2.COLOR_BGR2GRAY)
sift = cv2.xfeatures2d.SIFT_create()
kp1, dc1 = sift.detectAndCompute(img1, None)
kp2, dc2 = sift.detectAndCompute(img2, None)
bf = cv2.BFMatcher(cv2.NORM_L1, crossCheck=True)
matches = bf.match(dc1, dc2)
matches = sorted(matches, key=lambda x:x.distance)
mathced_img = cv2.drawMatches(img1, kp1, img2, kp2, matches[:50], img2, flags=2)
# kp = sift.detect(gray,None)
# img=cv2.drawKeypoints(gray,kp,None,flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
plt.figure(figsize=(20, 20))
plt.imshow(mathced_img)
plt.show()

Ref.
.