CG - Rasterizer

지금까지 Vertex shader와 Vertex shader가 하는 역할인 Object space부터 World space와 Camera space를 거쳐 Clip space까지의 변환을 배웠다. Vertex shader는 Clip space의 점들의 좌표을 Rasterizer에 넘겨준다. 그러면 Clip space의 점들을 다시 조립(assemble)한다. 그래서 하나의 삼각형이 스크린에 나타나게 된다. 그러면 삼각형의 픽셀들을 점유하면서 색깔(정보)들을 보여주며, 픽셀 위치마다 fragment를 정의하게 된다. Rasterizer는 여기서 fragment를 만드는 것이 주요 임무이다.
Rasterizer는 Clipping, Perspective division, Back-face culling, Viewport transform, Scan conversion을 진행한다. 여기서 모르는 단어들은 이번 포스팅에서 다룰 예정이다.
Clipping

세개의 삼각형 중에서 t2만이 view frustum에 들어온다. 그래서 다음 단계로 넘어갈 수 있지만 t3의 경우 바깥에 있는 부분이 있다. t3같은 경우에는 clip을 해야한다. 그래야만 다음 단계로 넘겨줄 수 있다.
이제 Clip space에서 보이지 않는 부분을 처리하는 방법과 screen에 어떻게 표현이 되는지 알아보자.
Vertex shader가 출력한 정점은 primitive로 assemble되고, 이 primitive는 스크린에 그려질 형태로 변환, 분해된다. 이를 Rasterization이라고 한다.
Perspective division

Camera space에서 Clip space로 옮기는 변환이다. (x, y, z, 1)은 Camera space의 좌표이다.
여기서 transform 후의 -z는 어떤 역할을 하는 걸까?

fovy, aspect, n, f가 간단하게 주어졌다고 해보자.
- fovy는 카메라가 바라보는 각도이다.
- aspect = 1은 x축은 아래 그림에서 잘 안보이니까 좌우방향으로도 90도의 view를 갖는다는 뜻이다.
- n은 평면에서 near plane 까지의 거리를 의미한다. z축에 놓인다. (z = -1)
- f는 평면에서 far plane 까지의 거리를 의미한다. 아래 그림에서는 2이다. (z = -2)
아래 그림처럼 아주 간단한 View frustum을 만들었다.


우리는 z의 역할을 알고 싶다. 이제까지는 빨간색 동그라미 쳐 진 부분이 다 1이었는데, 2로 넘어온다. 1이 아닌 값이 나오면 전체를 다 그 값으로 나눠주어야 한다.
P1, P2, Q1, Q2에 대해서 모두 Projection matrix를 곱해주면 위와 같은 결과(P1', P2', Q1', Q2')가 나온다. Projection matrix의 역할은 View frustum이 정육면체로 옮기는 것이었다. 그림1에서 보다시피 뒤에 있는 l1은 상대적으로 짧아지고, 앞에 있는 l2는 상대적으로 커보이게 하는 것이 특징이다.
그러면 여기서 z의 역할은 뭘까?
모든 꼭짓점들은 음수의 z축에 있기 때문에 z좌표 자체가 음수고, 여기에 -를 씌워주니까 전체적으로 양수가 된다. 그러면서 그게 평면으로부터 얼마나 멀리 떨어져 있는가를 나타낸다. 즉, Mproj P1의 빨간 동그라미 2는 P2보다 더 멀리 떨어져 있다는 이야기이다. 즉, 멀리 떨어져 있을수록 w좌표가 크다. 그 큰 w좌표를 1이 되게끔 다 w로 나눠주므로, 멀리 떨어져있는 것을 큰 값으롤 나누므로, 작아진다. 바로 이것이 원근법을 구현하는 단계이다.
Back-face culling
먼저 뒷면은 그대로 처리할 필요가 없다. Back-face culling은 실제 화면에 보이지 않는 부분들(뒷면)을 지우는 과정이다.
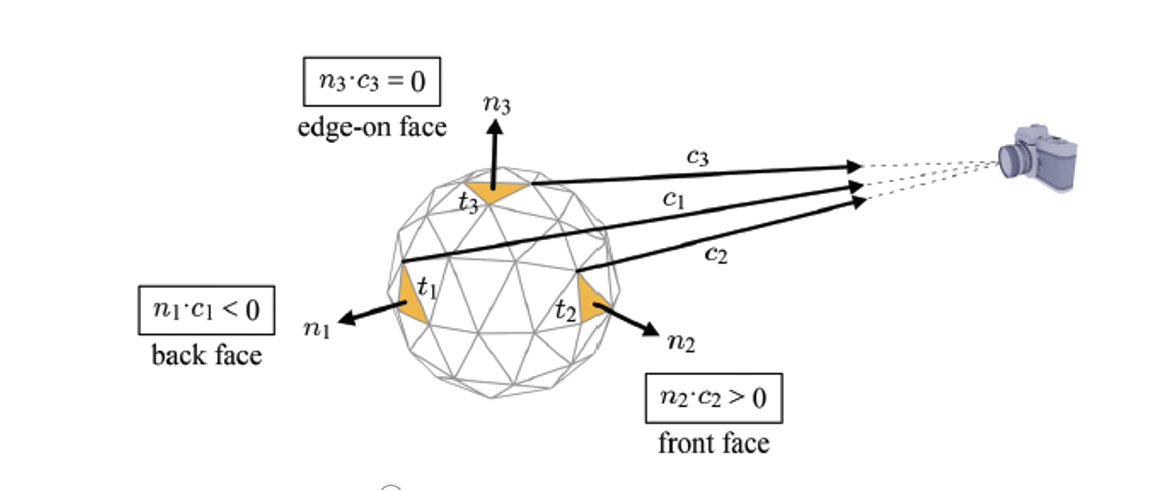
위의 구에서 t2의 좌표는 볼 수 있다. 그러나 t1은 볼 수 없다. 등지고 있다고 해서 back face라고 한다. 이렇게 안보이는 애들은 없에버려야 한다. 없에버리는 것을 culling이라고 한다. 이렇게 front face는 살리고, back face를 없에는 것이 Back-face culling이라고 한다.
위의 그림에서 edge-on face는 선분 하나로만 보이는 면이다. 이 삼각형의 normal을 n3라고 하고, 삼각형 꼭지점 하나를 잡는다. 그리고 카메라와 잇는다. 이를 c3라고 하자. 그럼 c3와 n3는 서로 수직인 벡터이다. 내적이 0이다. 이렇게 내적이 0이 되면 edge-on face라고 판단할 수 있다.
t2도 아무 꼭지점을 잡아서 카메라까지 잇는다. 그렇게 만들어진 벡터를 n2라고 하고 내적을 하면, 얼추 같은 방향이 나온다. 그럼 양수가 나온다. 양수가 나오면 front face이다.
t1도 똑같은 방식으로 내적하면 음수가 나온다. 이렇게 음수가 나오면 버리면 되겠다라는 결론을 얻을 수 있다.

하지만 이론과 실제 구현이 되는 것은 조금 다르다.

Projection matrix가 야기하는 불가피한 변화로 인해 구가 좀 찌그러져 있다. 여기서 z좌표는 무시하고 x와 y좌표만 따와보자. 우리는 이미 Camera space 이므로 z축이 투영선과 평행하다. 따라서 각각의 vertex에서 x,y 좌표만 보는 것이다. z를 무시한다는 것은 universal projection line을 따라서 투영하는 것과 같은 의미이다.
눈의 위치를 오른쪽에서 본다고 하자.
t2 삼각형에서 v1은 오른쪽에 있고 v3는 왼쪽에 있다. v1, v2, v3의 관계(반시계 방향)는 당연하게 보인다.
t1 삼각형에서 v1은 왼쪽에 있고 v3는 오른쪽에 있다. 이 경우에는 시계 방향(clock wise)으로 정렬되어 있다. 이처럼 시계 방향을 가지고 있으면, 나를 등지고 있으므로 back face가 된다.

v1, v2, v3는 폴리곤 메시에서 반시계 방향으로 순서되어 있다. 만약 z좌표를 무시한다면 v1에서 v2, v3로 가는 벡터 두개의 det를 구한다면 v1 v2 v3가 반시계 방향인지 시계 방향인지 알 수 있게 된다. 3차원일 때와 동일하게 ccw이면 앞면이 되고 3차원과 다르게 z축을 무시하면 cw가 되는 경우 cw이다.
Back-face culling은 아래의 과정을 거쳐서 한다.
- z좌표는 무시한다.
- x, y좌표만 가지고 2차원 평면에 그린다.
- 꼭지점들이 반시계 방향으로 나열 된다. -> front face
- 꼭지점들이 시계 방향으로 나열 된다. -> back face
이렇게 뒷면을 바라보는 삼각형은 모두 지울 수 있다. 다만 물체가 투명하거나 반투명하다면 뒷면을 아예 지우는것은 바람직 하지 않을 수 있다. 하지만 여기서는 지워야하는 경우를 가정하여 지우는 방법을 알아보았다.
Viewport Transform
마지막으로 Clip space에 정의된 물체가 실제 스크린에서 어떻게 보이는지 알아보기 위해 Viewport 변환을 진행하도록 하자.
실제 window 안에서 내가 그림을 그릴 영역을 Viewport라고 한다.

좌표를 지정 한 다음, 너비와 높이를 결정하면 Viewport 영역을 설정이 된다. minX, minY, Width, Height 4개의 파라미터가 필요하다.
3D는 화면 안쪽으로 파고드는 z축도 생각해야 한다. depth의 range를 설정해야 한다.
Viewport에서 screen space는 왼손 좌표계를 따른다.

다른 연산에 비해 훨씬 간단하다. [2 x 2 x 2] 정육면체를 [w x h x 1] 직육면체로 바꿔주자.
scaling matrix를 적용시키면 3D Viewport 크기로 축소 확대할 수 있다.
만약 screen이 (0,0,0)부터 (w,h,1)까지 차지한다면 translation matrix를 통해 원점으로 이동시키면 된다.

이렇게 Scaling과 Translation을 결합하면 Viewport transform이 완성된다.
Scan Conversion

이제 모든 정점들이 Viewport transform 을 통해 Screen space(화면)으로 나타났다.
왼쪽 그림에서 3차원 Screen space 안에 하나의 삼각형이 있다. 최종 Screen을 2차원 공간으로 표현하면 그 밑의 그림과 같다. 2차원 공간에서는 normal과 texture coordinate를 가지고 있다.(뒷장에서 배움)
이제 정점으로 이루어진 삼각형 내부의 점들(픽셀)들을 정의하고 이 점들의 normal을 어떻게 계산하는지 알아야 한다. 이를 Scan conversion이라고 한다. 이런 정점별 attribute는 삼각형의 변을 따라 선형보간된다. 이것들을 보간하는 것이 Scan conversion 단계에서 하는 것이다.
보간이라는 것은 빨간색에서 파란색으로 가거나, 흰색에서 검정색으로 갈 때 스무스하게 하는 것이다.

아래 세개의 꼭지점마다 RGB 칼라가 있다고 생각해보자.

- 먼저 vertex를 잇는 선 위에 점들(R1, R3)에 대해 보간을 진행한다. 왼쪽 그림의 빨간색에 해당한다.
- 다음으로 내부의 점들에 대해 빨간색 점 두개를 이용해 보간을 진행한다. R값의 차이를 구한다. 146-90 = 56
- y좌표에 대한 차이를 구한다. 6.5-0.9 = 5.6
- 변화율의 차이를 구하면 10이 나온다. 이것은 y가 1이 올라가는 만큼 얼마나 Red 값이 올라가는 지를 보여준다.
- x좌표에 대한 차이를 구한다.
- y가 1 증가할 때, x는 0.5 증가하는 것을 알 수 있다.
- 위의 정보들로 scan line 0.6에 대한 R 값을 계산할 수 있다.

왼쪽 그림을 보면 scan line의 교차점에 따라서 x값과 R값을 구할 수 있다. 세 선분에 대해서 모두 수행한다.
오른쪽 그림을 보자. 5개의 픽셀마다 R값을 할당하기 위해 두번 보간을 진행한다.
선형 보간을 2단계 했기 때문에 이를 bilinear interpolation이라고 한다.
Ref.
Introduction to Computer Graphics with OpenGL ES (J. Han)