CG - Spaces and Transforms
Affine Transform의 3가지 중요한 변환에 대해 알아보자.
Scaling (확대,축소)
먼저 볼 것은 Scaling이다. Scaling은 우리말로 축소, 확대이다.
2차원에서의 scaling을 먼저 보자. 간단하게 행렬로 표현하면 아래와 같다.
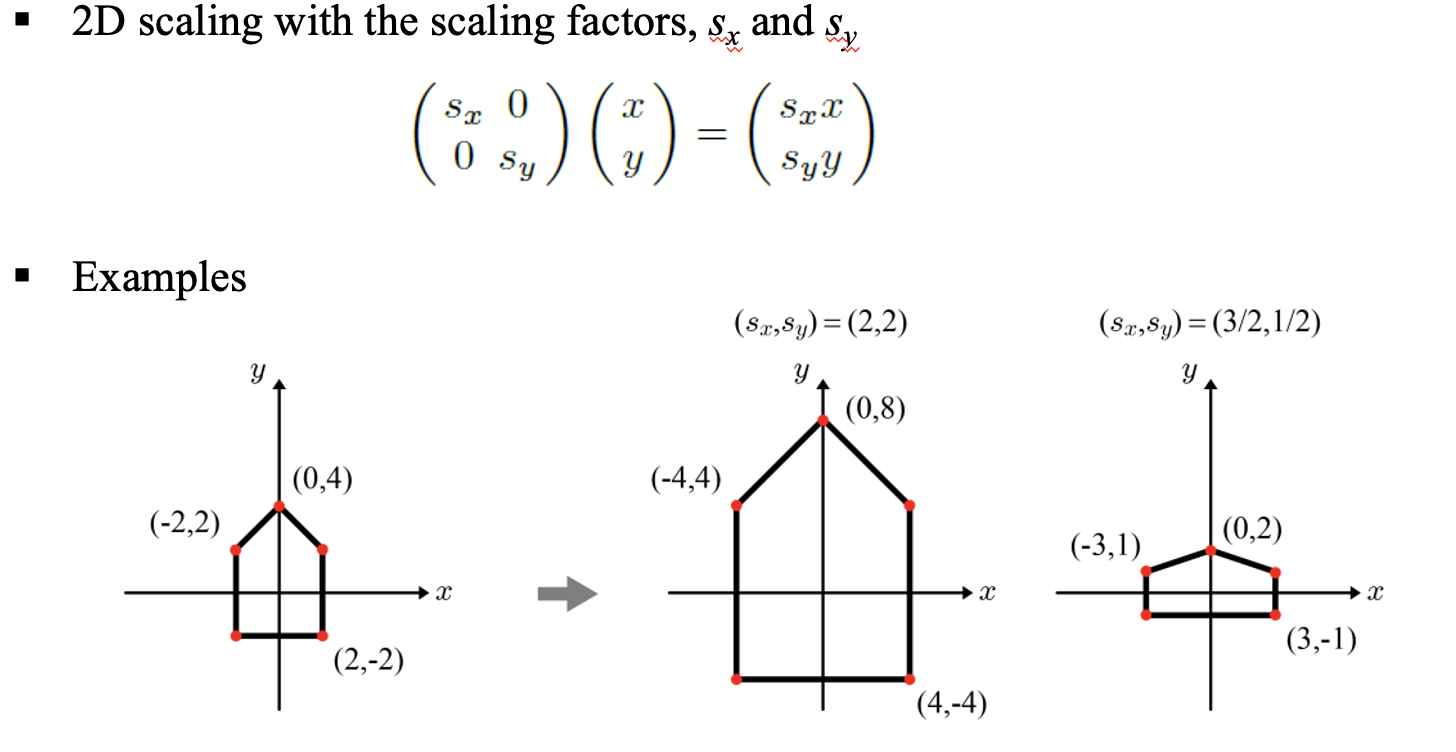
Rotation (회전)
다음으로 2차원 회전은 다음과 같다.
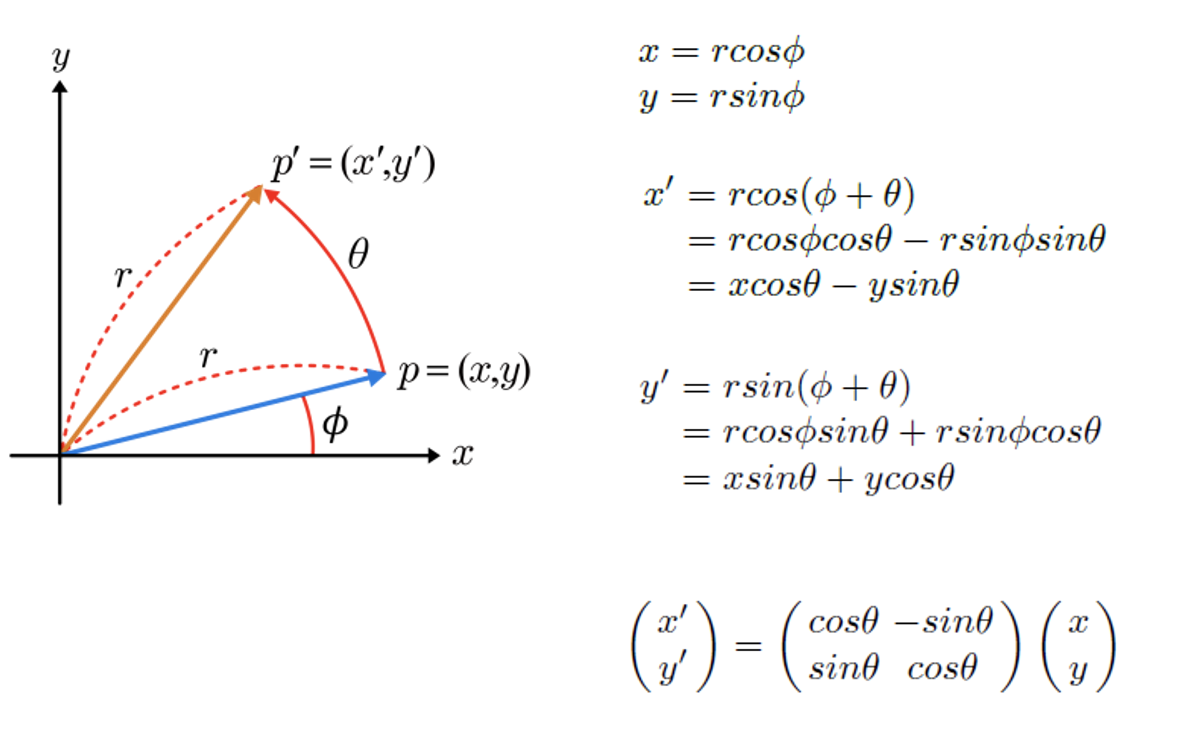
p 벡터의 좌표가 나와있을 때, 회전이 이루어졌을 때도 p' 벡터의 좌표를 알 수 있다.
기본적으로 반시계 방향으로 회전했을 때를 구한다.
Translation (이동)
지금까지 본 Scaling(확대/축소)와 Rotation(회전)은 선형변환이다. 하지만 이동(translation)은 선형 변환이 아니므로 위와 같은 행렬의 곱으로 표현할 수 없다. 선형 변환과 달리 이동은 일반적으로 행렬의 덧셈으로 표현되는데 동차좌표(homogeneous coordinate)를 이용하면 행렬곱으로 나타낼 수 있게 된다.

Transform composition
homogeneous coordinates는 굉장히 유용하다.

90도 rotation과 x축으로 7만큼의 translation을 위와 같이 표현할 수 있다.
먼저 쓰여지는 것이 오른쪽에 위치한다.
교환 법칙이 성립이 안됨을 유의하라.

이제 원점이 아닌 임의의 점을 상대로 rotation 해보자.
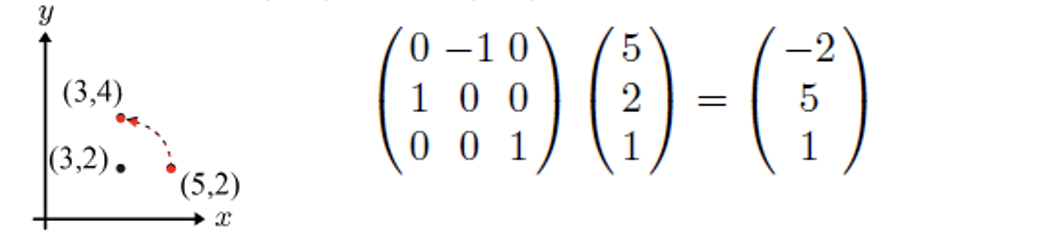
너무나 당연하게도 (5,2)를 넣었을 때 (3,4)로 가지 않는 것을 알 수 있다.
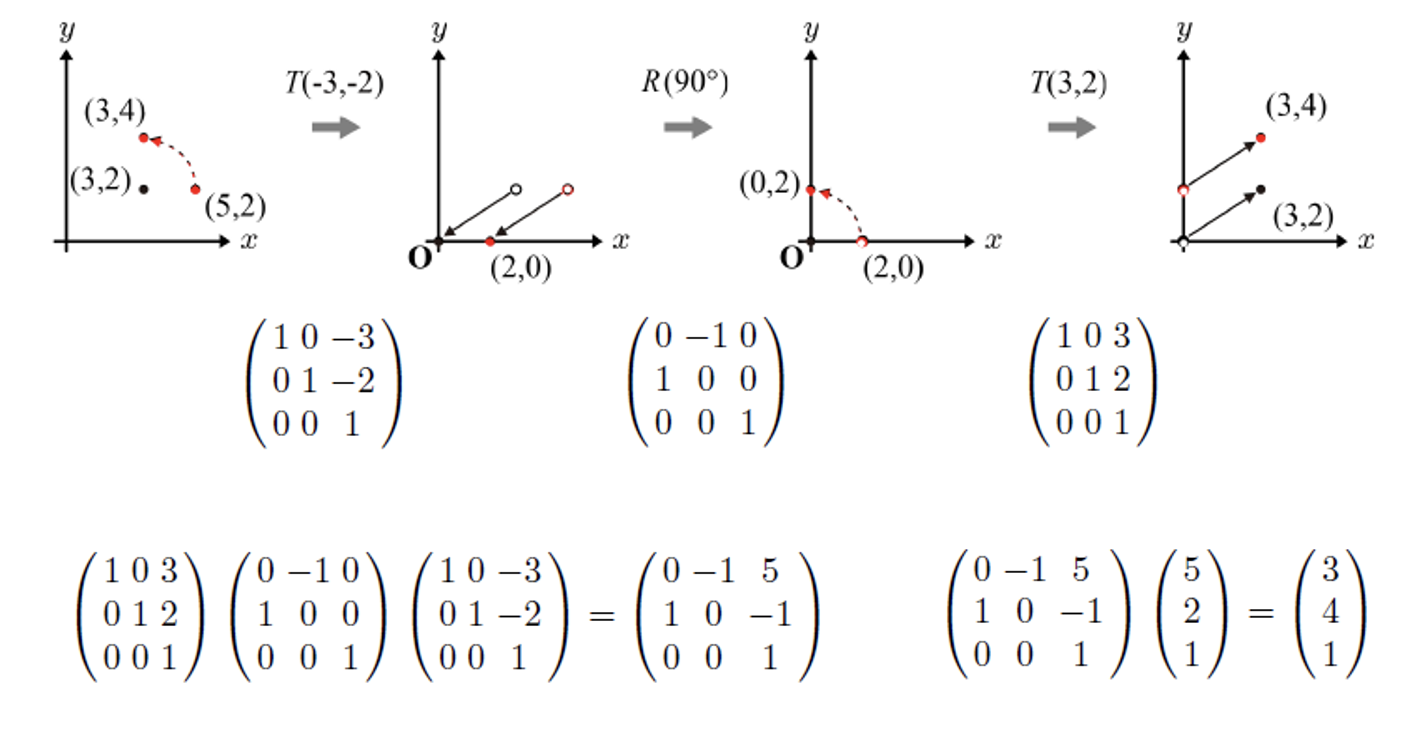
(5,2)를 회전축이 되는 (3,2)를 중심으로 회전하려면 원점으로 이동시켜 주어야 한다. 그리고 나서 회전한 후 다시 이동한만큼 원상 복구 해준다. 위의 식처럼 하나의 행렬로 표현할 수 있다.
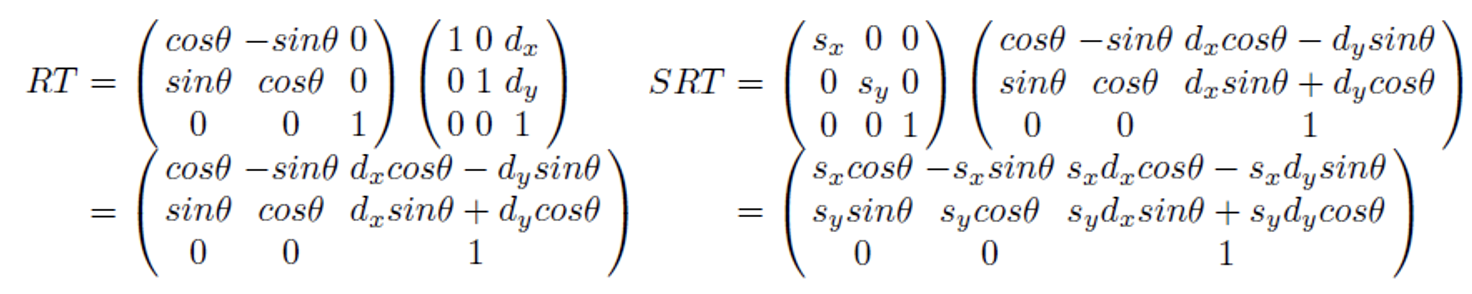
세번째 행은 항상 (0, 0, 1)로 고정이므로, 이를 무시하고 첫번째, 두번째 행을 유시하자.
우리는 이제 2행 3열의 matrix에서 2행 2열까지를 L이라고 하고, 3열을 t라고 약칭할 것이다. [L,t]
L은 이름이 암시하는 것처럼 Linear transform이 결합되어 있는 곳이다. 여기에는 입력으로 주어지는 translation이 못 들어간다. 세번째 column에만 개입될 수 있다.

translation은 3열에만 관련있다.
이것의 장점은 Rotation -> Translation 순서로 곱해도, Translation -> Rotation 순서로 곱해도 같은 결과가 나오는 것이다.
즉, 교환법칙이 성립이 되어 버린다.
이것이 Affine transform의 장점이다.
결론! Affine transform은 선형변환과 이동을 포함하는 변환이다.
n차원 Affine transform은 n+1차원의 행렬로 표현되므로 2차원 변환은 3x3 행렬로 표현된다.
3D 에서의 Transform
3D Scaling
이제 3차원을 보도록 하자. 3차원에서의 scaling도 2차원에서와 동일하다.

행렬의 대각성분을 scaling 해주면 된다.
3D Rotation

3D Rotation의 경우 2D과 조금 다르게 표현되는데 2D에서는 회전이 원점을 기준으로 반시계 방향으로 표현되는데, 3D의 경우 다양한 회전축 표현이 가능해진다.
대표적으로 x축 중심 Rotation과 z축 중심 Rotation을 보자.

x축을 기준으로 회전하는 주전자가 어떤 방식으로 회전하는지 직관적으로 알 수 있다.

y축 회전의 경우 Ry = mat3({cos,0,sin},{0,1,0},{-sin,0,cos}) 으로 표현된다.
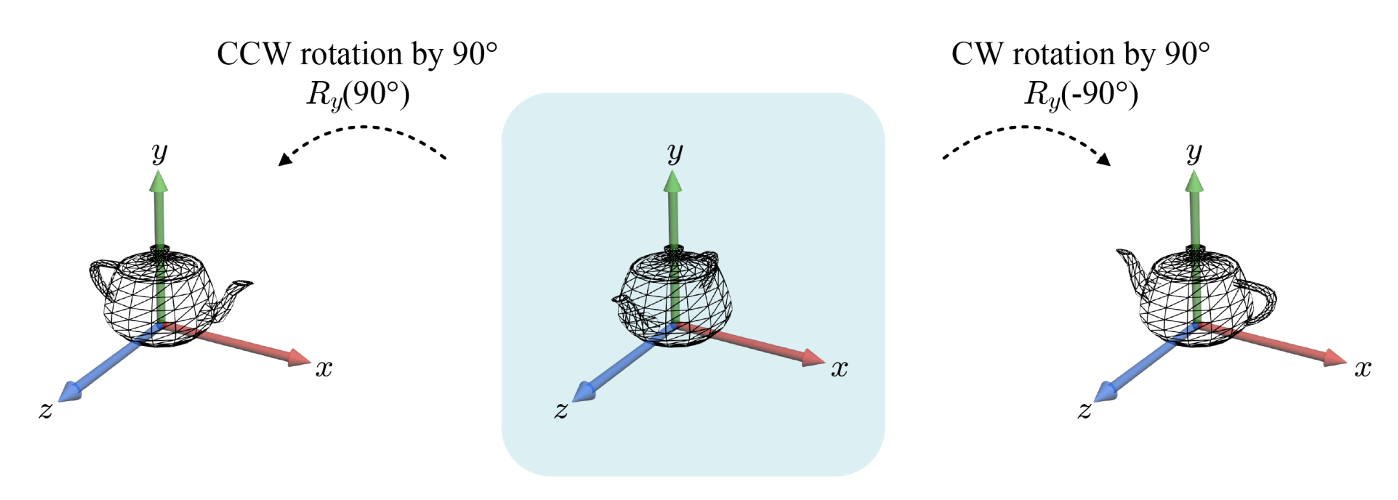
2차원과 마찬가지로 CCW(Counter Clock Wise)의 경우 양수로 표현되고 CW는 음수로 표현할 수 있다.
반시계 방향이 디폴트이다.
3D Translation
이제 translation을 보도록 하자.
2차원과 마찬가지로 affine transform의 경우 n+1 차원 행렬을 통해 표현할 수 있다.
만약 점(x,y,z)에 대해서 (dx,dy,dz)만큼 이동을 하고싶다면 다음과 같은 표현으로 이동할 수 있다.
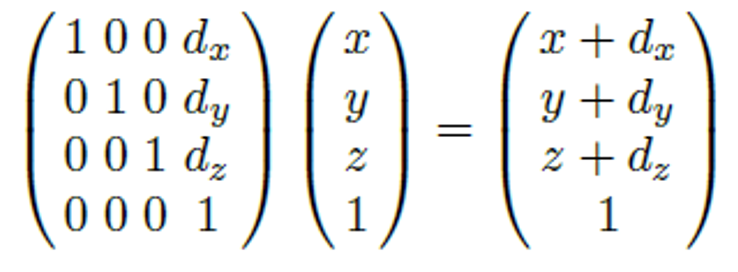
Application : World Transform
이제 이러현 변환을 어디에 사용하는지 알아보자.
물론 변환 행렬은 물체를 이동하고 변형시키는 많은 곳에 사용될 수 있지만 가장 대표적인 하나의 과정은 world transform이다.
물체를 모델링하는데 사용하는 공간을 object space라고 하는데 이 object space는 개별 물체를 정의하는 공간이므로 실제로 표현하고자 하는 스크린의 이미지를 모두 표현할 수 없다. 즉, 개별 물체가 존재하는 공간을 object space라고 하고 표현하고 싶은 world가 존재하는 공간을 world space라고 하기 때문에 우리는 world transform을 통해 object space에 정의되었던 물체들을 world space로 변환시켜야 한다. 즉, 단일한 객체 몇가지를 같은 공간에 넣어야 한다. 이러한 변환을 world transform이라고 한다.

우리는 구를 2배 넓히고, 주전자를 Rotation, Translation 시켜서 World space에 옮기고 싶다고 하자.


먼저 y축을 중심으로 Rotation 시키고, Translation 해주자.
행렬곱을 하고 나면, 위와 같은 행렬이 만들어진다.
주전자 주둥이 끝의 좌표를 통해 확인할 수 있다.
3D Affine Transform

이런 4x4 Affine transform에 있어서 항상 네번째 행은 (0,0,0,1)T이다.
나머지 3x4 행렬은 [L|t]로 표현되는데 왼쪽을 accumulated linear transform, 오른쪽을 accumulated translation으로 볼 수 있다.
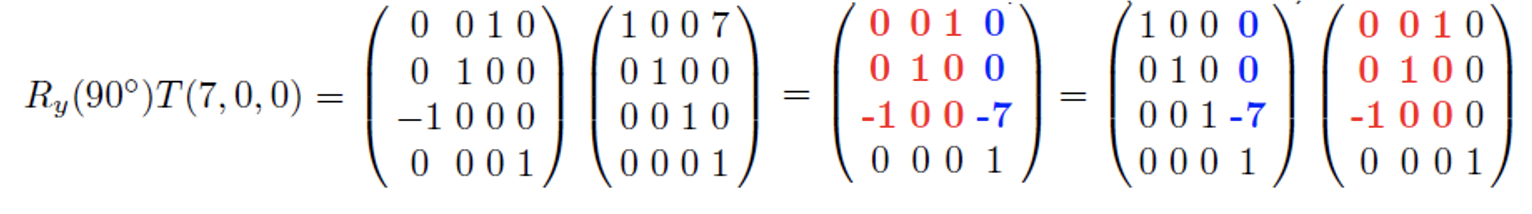
다만 이때 L는 t의 영향을 받지 않지만 t은 L의 영향을 받게된다. [L|t]로 변환된 행렬을 보면 L을 먼저 계산하고 t를 계산한 것으로 볼 수 있다. 즉 linear transform을 먼저 진행하고 translation한 형태가 된다.
Rotation and Object-space Basis

모델링이 끝나면, Object는 Object space와 결박되어 있어서 둘이 같이 움직인다. 분리가 안되고 붙어 있다.

World transform의 결과는 object space를 world space에 맞추는것으로 볼 수 있다. 즉, object는 자신의 object space와 일치하게되어 이동한다. {e1, e2, e3}는 world space의 basis를, {u, v, n}은 object space의 basis를 나타낸다고 하면 world transform 이후 E=u,v,n가 된다. 하지만 이후 object를 회전시키면 world space의 basis {u, v, n}은 그대로 유지되나 object space의 basis {e1, e2, e3}는 회전한다.
이때 회전을 R이라고 하자. 회전 후 basis는 다음과 같이 변한다.

중요한 것은 위에서 Object는 Object space와 딱 붙어서 간다고 했다.
여기서 말하고자 하는 것은 회전된 물체의 방향은 Object space basis의 방향으로 특징 지을 수 있다는 것이다.
즉, 물체의 회전이 적용되면 물체의 방향이 바뀐다. 그런데 어떠한 방향을 가질지는 {u, v, n}을 가지고 묘사할 수 있다.

Object space basis인 {e1, e2, e3}로 표현된 Object를 Rotation해도,
World space의 basis인 {u, v, n} 으로 표현할 수 있는 것을 확인할 수 있다!
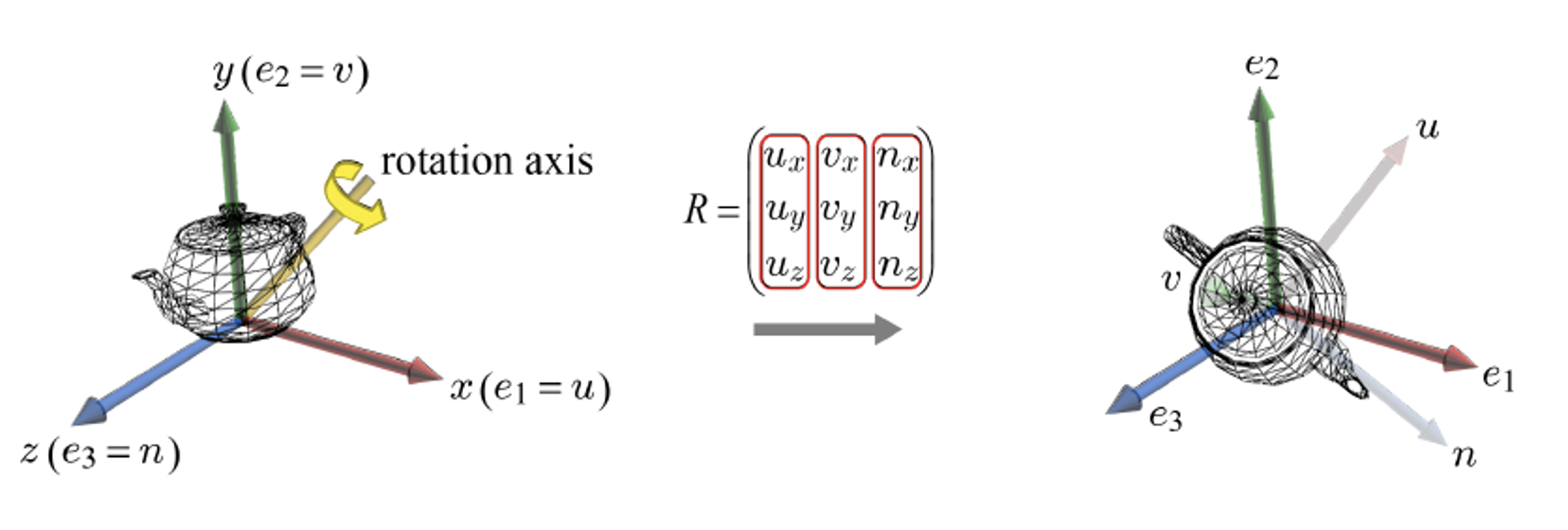
일반화 할 수 있다.
Ref.
Introduction to Computer Graphics with OpenGL ES (J. Han)