LSTM 이란?
목차
- 빈칸에 들어갈 단어는? (he, she)
- 간단한 RNN 구조
- 좀더 간략화한 RNN 구조
- Gradient descent weight optimization
- Error3 derivative caculation
- Gradient Vanishing
- Gradient Exploding
- Long sequence에 대한 해결책 : LSTM (Long Short Term Memory)
- LSTM : RNN에 memory cell 도입
- LSTM cell
- LSTM cell : forget mechanism
- LSTM cell : input mechanism
- LSTM cell : output mechanism
아래의 빈칸에 들어갈 단어는? (He/She)

정답 : He
빈칸의 이전 문장에서 John에 대한 이야기를 하고 있기 때문에, 빈칸에는 John을 가리키는 He가 들어가는 것을 알 수 있습니다.
이런 문제는 RNN으로 해결할 수 있는데, 만약 문장이 길어진다면 이러한 문제는 풀기가 힘들 수도 있습니다.
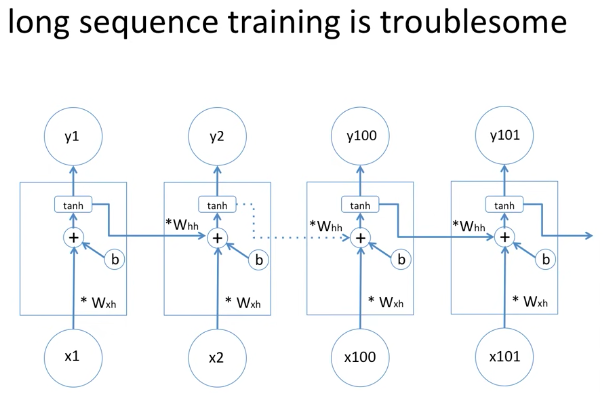
이러한 문제에 대해서 파악하고 솔루션으로 나온 것이 바로 LSTM 입니다.
간단한 RNN 구조

3개의 input인 x1, x2, x3가 있다고 했을 때,
RNN은 Supervised learning으로 답이 되는 target과 prediction의 차이인 Error를 줄여가며 학습을 하는 구조입니다.
좀더 간략화한 RNN 구조
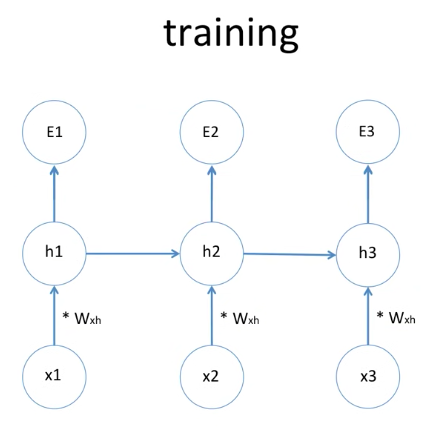
좀더 간략화 해 보면, 이렇게 input인 x1, x2, x3가 있고
hidden state가 있고
Error가 있습니다.
그리고 가중치는 w라고 표시가 되어 있습니다.
이렇게 RNN은 학습이 진행이 됩니다.
Gradient descent weight optimization
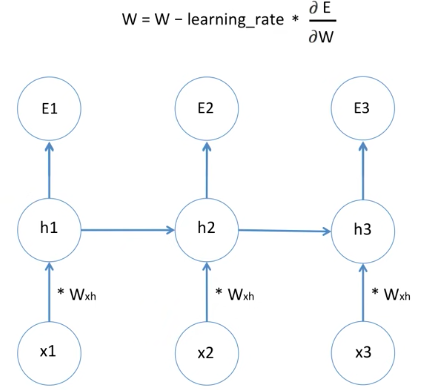
딥러닝은 예측값과 실제값의 차이가 최소가 되는 weight 값을 찾는 과정이고,
그 weight 값을 찾기 위해서 주로 gradient descent를 사용합니다.
그리고 RNN 역시 gradient descent를 사용합니다.

weight 값을 구하는 방법은
새로운 weight는 기존의 가중치에서 learning rate와 Error를 weight로 미분한 값을 빼면서 구할 수 있습니다.
이 Error를 weight로 미분한 값은 Error1의 미분값, Error2의 미분값, Error3의 미분값과 더한 것과 같습니다.
Error3 derivative caculation
E3을 가중치로 미분한 값을 구하는 과정은 Chain Rule로 진행됩니다.
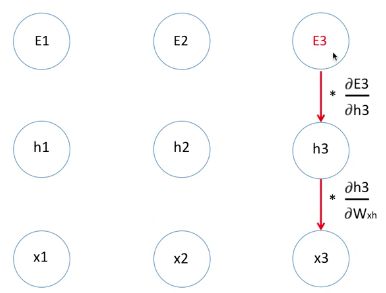

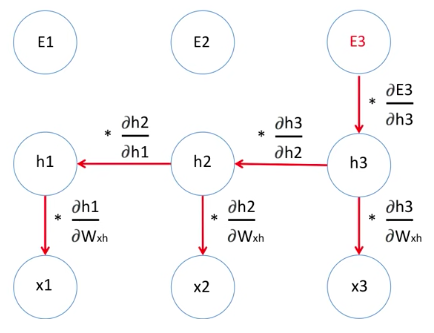

E3를 가중치로 미분한 값을 구할 수 있습니다.
Gradient Vanishing

weight를 구하기 위해서 미분값을 여러차례 곱하게 되는데, 짧은 sequence 같은 경우에는 큰 문제가 되지 않습니다.
그러나 긴 sequence의 경우에는, 예를 들어 100개 이상의 단어가 있다고 할 때, 100번 정도의 Chain rule로 인한 곱하기를 하게 됩니다.
만약 Chain Rule로 인한 미분값이 1보다 작게 되면, 이것을 계속 100번 넘게 곱하게 되면 0에 가까워 집니다.

이럴 경우 새로운 weight는 기존의 weight와 거의 차이가 없게 됩니다.
즉 학습을 길게 하더라도 weight 값이 거의 변하지 않게 됩니다.
다시 말해 학습이 길어지고 비효율적이게 됩니다.
이것을 바로 Gradient vanishing 이라고 합니다.
Gradient Exploding
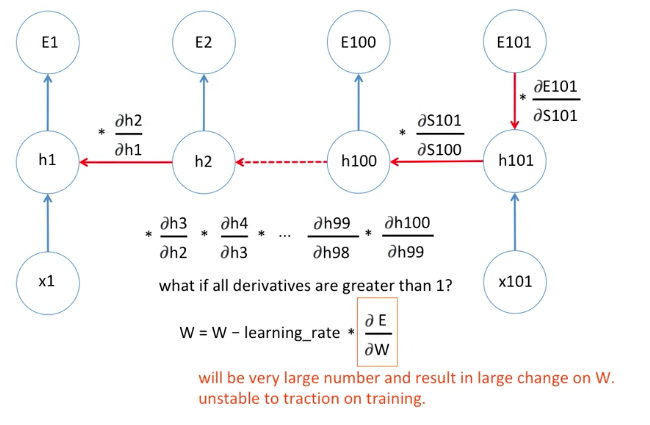
반대로 미분값이 1보다 크다고 했을 때,
예를 들어 2라고 가정하면, 이것을 100번 곱하면 2^100 이니까 상당히 값이 커지게 됩니다.
그러면 새로운 weight 값은 기존의 weight 값과 상당히 달라지게 됩니다.
그렇게 되면 training이 왔다리 갔다리 하면서 Gradient 값이 한 곳으로 가지 못하게 됩니다.
이것을 바로 Gradient exploding 이라고 합니다.
Long sequence에 대한 해결책 : LSTM (Long Short Term Memory)
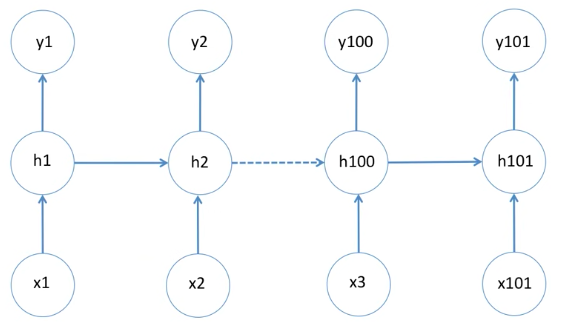
그래서 이 Long sequence 문제를 극복하기 위해서 나온게 바로 LSTM 입니다.
LSTM : RNN에 memory cell 도입
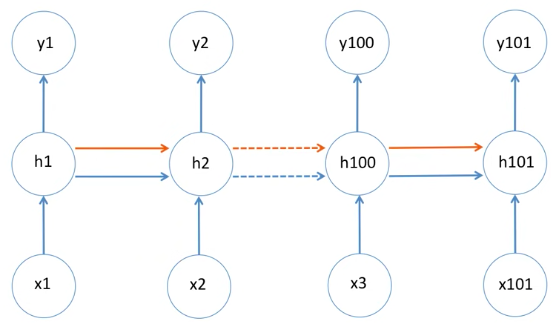
위의 RNN 구조와 다르게 LSTM의 구조에서는 새로운 빨간색 라인이 추가된 것을 확인할 수 있습니다.
이 라인을 memory cell 이라고 합니다.
한 문장을 예시로 봐봅시다.
아래의 문장에 John에 대한 이야기를 하는 문장이 있습니다.

그런데 여기서 John에 대한 이야기를 쭉 하다가 Jane에 대한 이야기를 하면 어떻게 될까요?

여기에서 빈칸을 채우라고 했을 때, memory cell은 John에 대한 정보를 잊어버리고,
새로 들어온 Jane에 대한 정보를 기억하고 있어야 합니다.
그리고 she를 출력해주어야 합니다.
LSTM cell
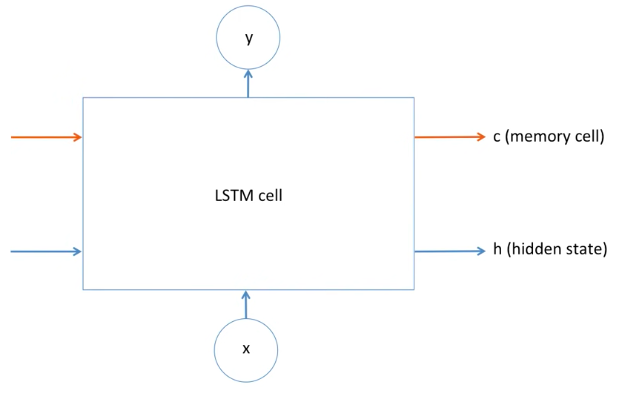
그러면 LSTM은 도대체 어떻게 John과 Jane을 구분해서 출력해줄까요?
LSTM에는 어떠한 정보를 잊는 메커니즘, 어떠한 정보를 기억하는 메커니즘, 이러한 것들이 LSTM cell 이라는 곳에 들어있습니다.
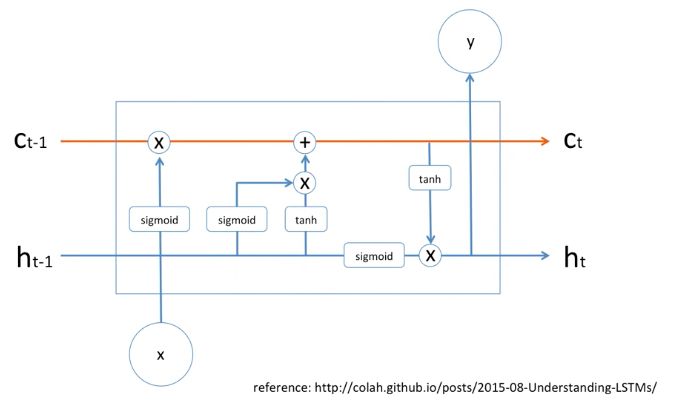
당연히 LSTM은 딥러닝 모델이고, 딥러닝 모델은 수학적인 모델이기 때문에,
어떠한 정보를 잊고 기억하고 이러한 것들은 모두 수학적인 공식입니다.
위의 그림은 LSTM의 간단한 모델이고, LSTM의 간략한 메커니즘을 보여주고 있습니다.
cell에 빨간색 라인과 파란색 라인이 들어오고 output도 출력하지만,
빨간색 라인과 hidden state의 파란색 라인은 계속해서 옆에 있는 cell로 전파가 되게 되어있습니다.
LSTM cell : forget mechanism
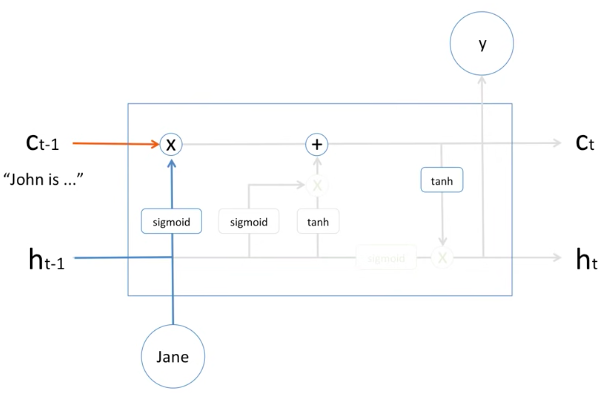
먼저 알아야 될 것은 어떤 정보는 잊고, 어떤 정보는 기억을 해야한다는 것인데, 먼저 어떻게 잊는지 봐봅시다.
과거의 문장들이 "John is ..." 등의 John에 대한 정보들이 있다고 합시다.
이것은 memory cell에 저장이 되어 있습니다. (Cell t-1)
이때, 새로운 단어인 Jane 이라는 정보가 들어왔을 때, 과거의 hidden state인 h t-1 과 같이 들어오면서,
Activation function인 시그모이드 함수를 거쳐서 들어온 것을 확인할 수 있습니다.
여기서 시그모이드 함수로부터 나온 출력값은 0부터 1까지의 값인 확률값 입니다.
이 말은 즉슨, 과거의 정보를 몇 퍼센트만 기억을 하라 입니다.

만약에 여기에 Jane이 들어오면, 이 시그모이드의 결과값으로 20%가 나왔다고 한다면,
그러면 과거의 모델이 기억하고 있는 것에 20%만 남겨놔라 라는 뜻이 됩니다.
즉, 까먹어라 라는 메커니즘을 수학적으로 구현했다고 볼 수 있습니다.
당연히 학습 과정에는 weight와 bias가 또 학습이 되게 되어있습니다.
그러므로 새로운 Jane이라는 정보가 들어왔을 때, 과거의 정보는 20%만 간직해라 라고 해서, 이렇게 과거의 정보가 어느정도만 넘어온 것을 확인할 수가 있습니다.
LSTM cell : input mechanism
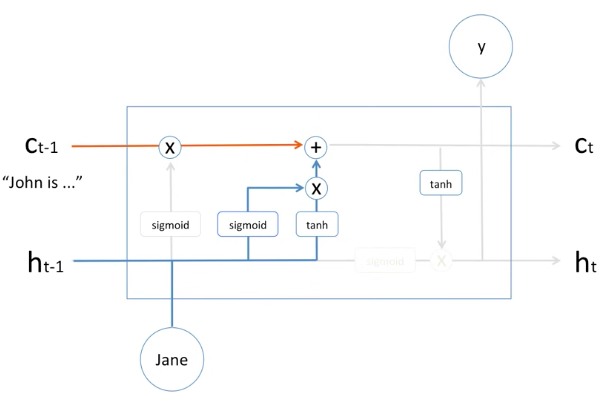
그러면 과거의 정보는 어느정도 잊었고, "야, 이 정보는 꼭 기억해야돼" 라는 정보는 어떻게 처리하는지 봅시다.
위의 그림은 그 부분을 도식한 그림입니다.
과거의 hidden state와 현재의 Jane 이 들어와서 Activation function인 sigmoid와 하이퍼볼릭 탄젠트(tanh)를 거친 후에 서로 곱해져서 과거의 memory cell인 Cell t-1 과 더해집니다.
즉, 새로운 정보가 memory cell에 수학적으로 더해지는 과정입니다.
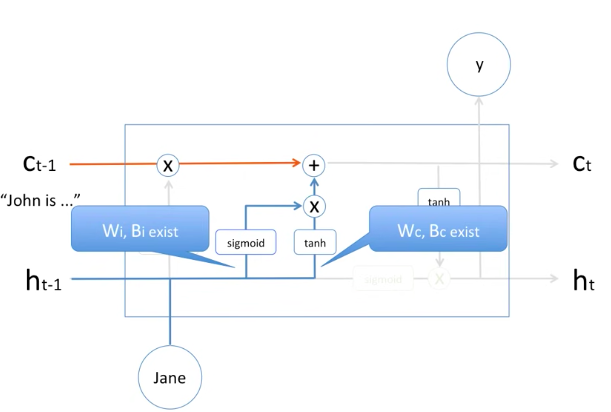
물론 여기에 sigmoid와 tanh 앞에 weight와 bias가 학습되게 되어 있습니다.
이것 역시 학습과정을 통해서 optimize 됩니다.
LSTM cell : output mechanism

마지막으로 output mechanism은, 이것 역시 RNN cell 이니까, 정보를 출력하고 state를 다음 cell에 전달을 해야겠죠?
그러면 memory cell에 있는 정보가 tanh를 거친 후에 들어오고,
그리고 hidden state와 현재의 정보가 sigmoid를 통해서 들어오고,
서로 곱한 다음에,
이 곱해진 값이 output인 she로 출력이 되고,
또한 이 값이 다음 hidden state로 넘어가는 것을 확인할 수 있습니다.
이런식으로 LSTM 모델이 학습됩니다.
Ref : https://www.youtube.com/watch?v=bX6GLbpw-A4