Deep Neural Network - Back Propagation
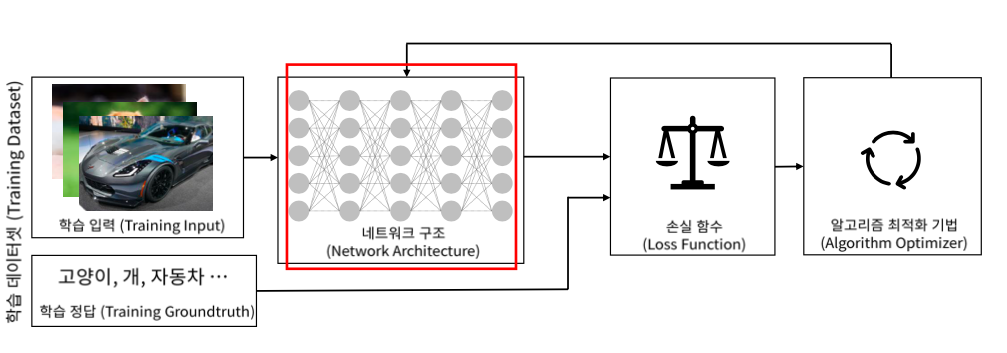
Shallow Neural Network 에 이어서 Deep Neural Network에 대해서 배워보자.
뉴런

입력이 들어왔을 때 가중치와 bias를 곱해주고 Summation 한 다음
Activation function을 이용해서 Nonlinear 연산으로 출력을 하는게 뉴런이다.
Shallow Neural Network

Hidden layer 에서는 dense layer(=fully connected layer)를 통해 계산한다.
보통 SNN의 Hidden layer에서는 Sigmoid를 이용한다.
Output layer의 경우에서 사용되는 activation function은 linear 또는 softmax를 이용한다.
softmax를 이용하면 확률로 나오면서 classification에 이용된다.
Deep Neural Network
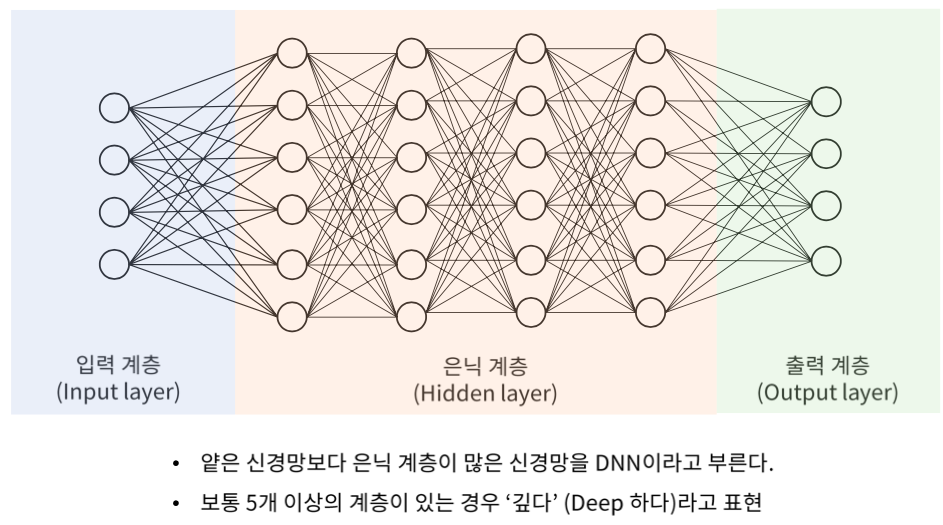
DNN은 무엇이 다를까?
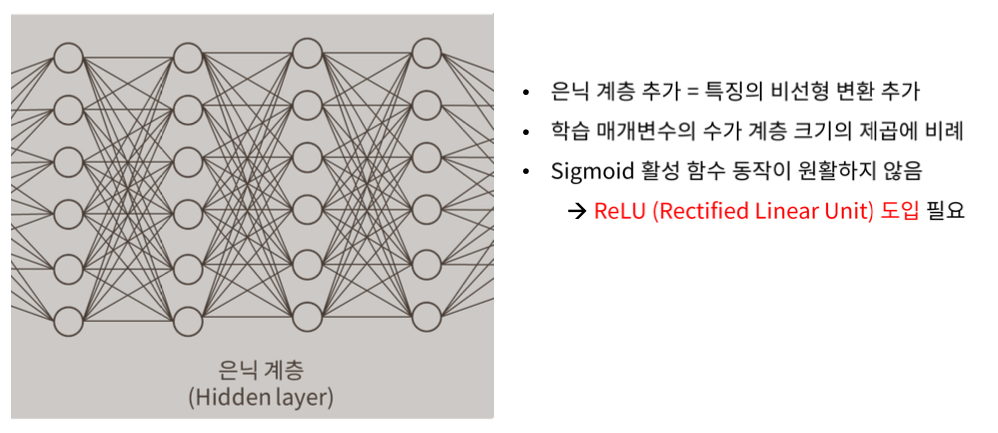
Hidden layer를 추가함으로써 점점 더 Linear하게 만든다.
학습 parameter의 수가 layer 수의 제곱에 비례한다. 따라서 매우 빠르게 학습 parameter가 증가한다.
기존의 SNN의 Sigmoid 함수가 원활치 못하기 때문에, 기울기 소실문제가 발생하기 때문에 ReLU(Reactified Linear Unit) 함수를 이용한다.
알고리즘 학습법과 미분
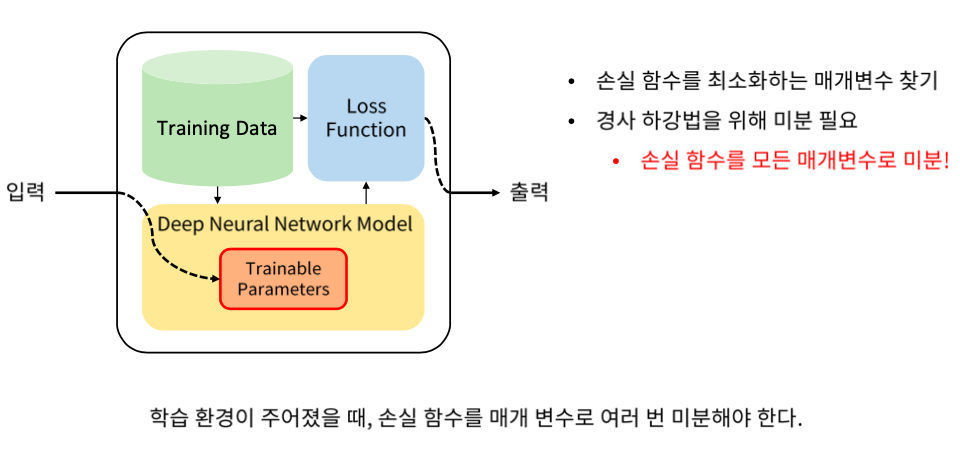
알고리즘을 학습할 때
Training data, Loss function 그리고 Model이 학습을 할 때 결정되어야할 환경이다.
Training data는 DNN에 입력되는 것과 정답 두가지로 구성되어 있다.
모델에 넣었을 때 출력을 받고 정답과 Loss function으로 비교해서 최종적으로 얼마나 잘 못하고 있는지 손실함수 출력을 내는 형태로 되어있다.
우리가 해야하는 것은 출력값을 입력값들로 미분을 해야한다.
미분을 해야 Adam 이나 Gradient Discent 등의 방법들을 이용해서 최적화를 진행할 수 있기 때문에 미분을 해야한다.
의존성이 있는 함수의 계산
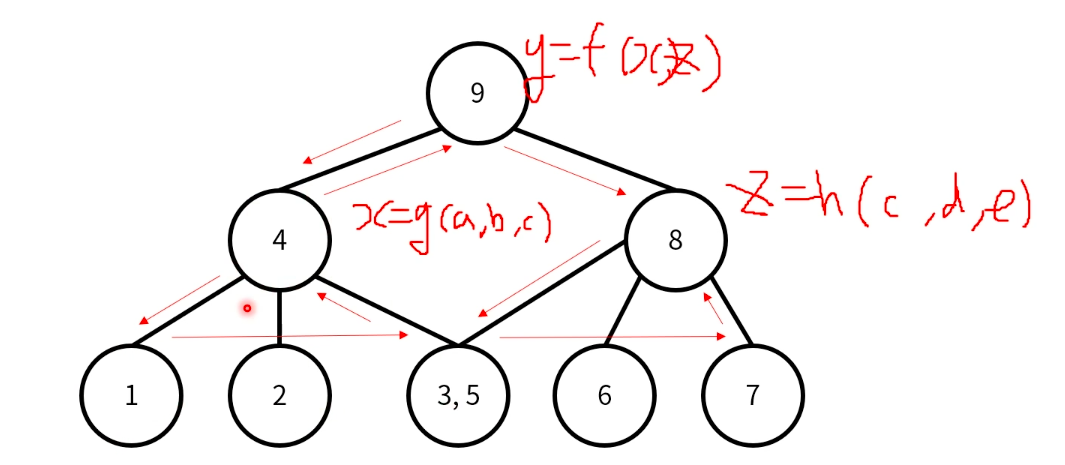
c를 구할 때 동일 연산이 2회 필요하므로, 중복되는 계산이 1회 발생한다.
Dynamic Programming

겹치는게 하나만 있으니까 시간이 덜 걸리지만, 여러개가 겹치면 시간이 아주 오래걸린다.
따라서 DP를 이용해야 한다.
연쇄 법칙 (Chain Rule)

연쇄법칙은 g(f(x))' = g'(f(x)) f'(x) 와 같은 개념이다.
DNN의 미분
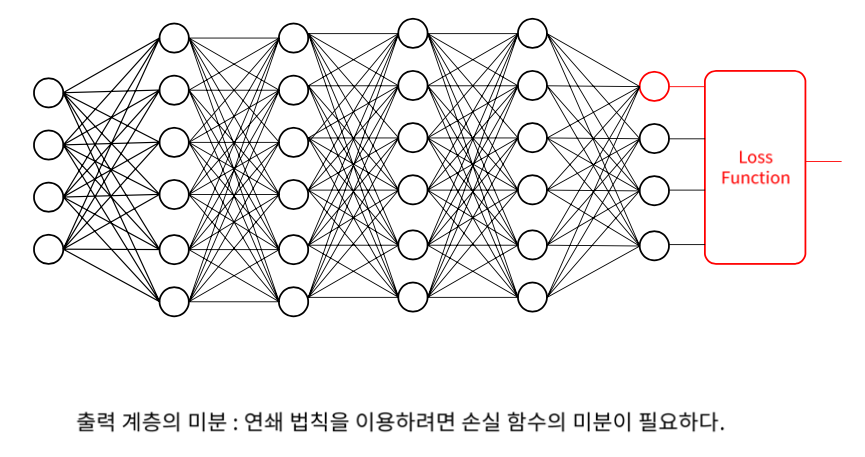
Output Layer의 미분은 Loss function을 미분할 수 있어야 한다.
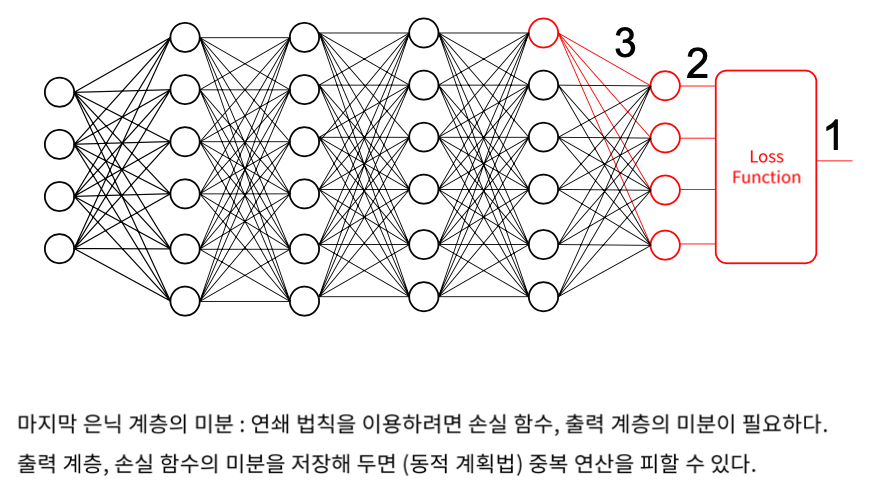
1을 3의 weight로 미분하려면
1을 2로 미분하고 2를 3으로 미분해서 곱한다.

Hidden layer에 연결되어있는 모든 미분값들을 다 알아야 한다.
순방향 추론 (Forward Inference)

이렇게 쭉 오는 것을 순전파(foward)라고 하며 말 그대로 앞쪽으로 input 값을 전파, 보내는 것이라고 보면 된다. 하지만 우리가 임의로 한 번 순전파 했다고 출력 값이 정확하지는 않을 것이다. 우리가 임의로 설정한 가중치 값이 input에 의해서 한 번 업데이트 되긴 했지만 많은 문제가 있을 수 있다.
역전파 학습법 (Back Propagation)

역전파 방법은 결과 값을 통해서 다시 역으로 input 방향으로 오차를 다시 보내며 가중치를 재업데이트 하는 것이다. 물론 결과에 영향을 많이 미친 노드(뉴런)에 더 많은 오차를 돌려줄 것이다.

위의 그림을 보면 Input이 들어오는 방향(순전파)으로 output layer에서 결과 값이 나온다. 결과값은 오차(error)를 가지게 되는데 역전파는 이 오차(error)를 다시 역방향으로 hidden layer와 input layer로 오차를 다시 보내면서 가중치를 계산하면서 output에서 발생했던 오차를 적용시키는 것이다.
한 번 돌리는 것을 1 epoch 주기라고 하며 epoch를 늘릴 수록 가중치가 계속 업데이트(학습)되면서 점점 오차가 줄어나가는 방법이다.

위의 그림을 보면 Output layer에서 나온 결과 값이 가진 오차가 0.6이라고 되어 있다. 이전 노드(뉴런에서) Output layer에 각각 3, 2라는 값을 전달하였기 때문에 Ouput의 Error에 위 노드는 60%, 아래 노드는 40% 영향을 주었다고 볼 수 있다. 균등하게 가중치를 나눠줄 수 있지만 영향을 미친 만큼 오차를 다시 역전파하는게 맞는 것 같다.
error 0.6을 0.6, 0.4를 곱하니 위 노드에는 error가 0.36이, 아래 노드에는 0.24가 전달된다.
오차 역전파는 말 그대로 이렇게 오차를 점점 거슬러 올라가면서 다시 전파하는 것을 의미한다.
역전파 학습법 : 순방향 추론을 먼저 하고 뒤쪽 방향으로 연쇄법칙을 이용해서 미분하며 곱해나는 것
그러면 전체에 대한 gradient가 하나 나오게 된다.
Reference
www.slideshare.net/RickyPark3/2linear-regression-and-logistic-regression